Exercícios sobre números irracionais
Marque a alternativa correta sobre o conjunto dos números irracionais.
A) O conjunto dos números irracionais é uma ampliação do conjunto dos números racionais, contendo os números racionais e também os números que não podem ser escritos como fração.
B) O conjunto dos números irracionais é formado por todos os números que não podem ser escritos na forma de fração. Assim, raízes não exatas e dízimas não periódicas fazem parte desse conjunto.
C) O conjunto dos números irracionais é formado por todos os números que podem ser representados na forma de fração, como os números decimais.
D) O conjunto dos números irracionais e o dos racionais são o mesmo conjunto.
Alternativa B. De fato, o conjunto dos números irracionais é formado por todos os números que não podem ser representados como fração, e os exemplos citados estão corretos.
Dos números irracionais a seguir, qual deles pertence ao intervalo 2 e 3?
A) Π
B) √2
C) √3
D) -3,123124458901...
E) √6
Alternativa E. Analisando as alternativas, o único que está entre 2 e 3 é √6, que possui representação decimal igual a 2,44949074….
Classifique as afirmações a seguir como verdadeiras (V) ou falsas (F).
I – Um número inteiro pode ser um número irracional.
II – O conjunto dos números racionais tem intersecção vazia com o conjunto dos números irracionais.
III – O conjunto dos números irracionais está contido no conjunto dos números reais.
IV – O conjunto dos números reais está contido no conjunto dos números irracionais.
V – Qualquer raiz quadrada tem como resultado um número racional.
Marque a alternativa que contém a classificação correta das afirmativas respectivamente:
A) F, V, F, V, V
B) F, V, V, F , F
C) F, V, V, V ,F
D) F, F, F, F, V
E) V, F, F, V, V
Alternativa B
I → Falsa, pois um número inteiro é racional e, portanto, não pode ser irracional.
II → Verdadeira, pois não existe um número que seja racional e irracional ao mesmo tempo.
III → Verdadeira, pois o conjunto dos números reais é formado pela união dos racionais com o irracionais.
IV → Falsa, pois os números reais contêm os números irracionais, e não o contrário.
V→ Falsa, sendo exemplos o √2 e qualquer raiz não exata.
Dos números a seguir, podemos afirmar que todos são irracionais, exceto:
A) 8,1011121314152034….
B) √3
C) -√5
D) 3,141592
E) Π
Alternativa D. O único número da lista que não é irracional é 3,141592, que, no caso, é um decimal exato.
Sobre o conjunto dos números irracionais, julgue as afirmativas a seguir:
I – A soma de dois números irracionais é sempre um número irracional.
II – O produto entre dois números irracionais é sempre um número irracional.
III – Todo número real é um número irracional.
Após julgar as afirmativas, podemos afirmar que:
A) somente a afirmativa I é verdadeira.
B) somente a afirmativa II é verdadeira.
C) somente a afirmativa III é verdadeira.
D) somente I e II são verdadeiras.
E) todas as afirmativas são falsas.
Alternativa E.
I → Falsa. Nem sempre é um número irracional, como o caso de √2 + ( –√2) = 0 (zero é um número racional).
II→ Falsa. A multiplicação de dois números irracionais pode resultar em um número racional, como √2×√2 = 2, um número racional.
III → Falsa, pois o conjunto dos números reais é formado pela união dos números racionais e irracionais, então há números que são reais e não são irracionais.
Das alternativas abaixo, determine qual delas melhor se aproxima do valor do número irracional √8.
A) 2,830
B) 2,828
C) 2,826
D) 2,827
E) 2,831
Alternativa B.
Para encontrar o valor que mais se aproxima de √8, vamos calcular cada uma das alternativas ao quadrado, considerando três casas decimais:
2,830² = 8,008
2,828² = 7,997
2,826² =7,986
2,827² =7,991
2,831² =8,014
Note que o valor mais próximo é o da letra B: 2,828.
Das raízes quadradas a seguir, encontre aquela que corresponde a um número irracional.
Alternativa C.
Para encontrar qual corresponde a um número irracional, é necessário realizar a fatoração:
a) Racional.
1296| 2
648| 2
324| 2
162| 2
81| 3
27| 3
9| 3
3| 3
1| 1296 = 24 × 34
Sendo assim, a√1296 = √(24 × 34) = 2² × 3² = 4 × 9 = 36, logo é um número racional, pois existe raiz exata.
b) Racional.
2704|2
1352|2
676|2
338|2
169|13
13|13
1| 2704 = 24×13²
Sendo assim, temos que √2704 = √(24 × 132) = 2² × 13 = 4 × 13 = 52.
c) Irracional.
1875| 3
625| 5
125| 5
25| 5
5| 5
1| 1875 = 54 × 3
Note que o expoente de três é 1, logo não será possível extrair a raiz dele, então esse número é irracional, podendo ser representado como 25√3.
d) Racional.
2304|2
1502|2
576|2
288|2
144|2
72|2
36|2
18|2
9|3
3|3
1| 2304 = 28 × 3²
Então, √2304 =√(28 × 3²) = 24 × 3 = 16 × 3 = 48.
O perímetro de um terreno que possui o formato de um quadrado com área medindo 90 m², em metros, é igual a?
A) 7√10 metros
B) 3√10 metros
C) 12√10 metros
D) 5√10 metros
E) √10 metros
Alternativa C.
Para encontrar o valor do lado, basta calcular a raiz quadrada de 90.
l = √90
Sabemos que 90 = 9 ×10 e que √9 = 3, então o valor do lado será:
l = 3√10
Para calcular o perímetro, basta multiplicar por 4, logo a área desse terreno é:
4 ×3√10 = 12√10 metros
Qual das afirmativas a seguir é verdadeira?
A) √20 é irracional e √200 é racional.
B) √40 é irracional e √400 é racional.
C) √50 é irracional e √500 é racional.
D) √25 é irracional e √250 é racional.
E) √100 é irracional e √10 é racional.
Alternativa B.
A única alternativa que contém, respectivamente, um número racional e um irracional é a alternativa b, pois √40 é irracional e √400 é racional.
(UEL) Observe os seguintes números.
I. 2,212121…
II. 3,212223…
III. π/5
IV. 3,1416
V. √-4
Assinale a alternativa que identifica os números irracionais.
A) I e II
B) I e IV
C) II e III
D) II e V
E) III e V
Alternativa C.
Dos números listados, os únicos que são irracionais são:
II — dízima não periódica;
III — π é uma dízima não periódica e π/5 também.
(UFF) Segundo o matemático Leopold Kronecker (1823-1891), “Deus fez os números inteiros, o resto é trabalho do homem.” Os conjuntos numéricos são, como afirma o matemático, uma das grandes invenções humanas. Assim, em relação aos elementos desses conjuntos, é correto afirmar que:
A) o produto de dois números irracionais é sempre um número irracional.
B) a soma de dois números irracionais é sempre um número irracional.
C) entre os números reais 3 e 4, existe apenas um número irracional.
D) entre dois números racionais distintos, existe pelo menos um número racional.
E) a diferença entre dois números inteiros negativos é sempre um número inteiro negativo.
Alternativa D.
a) → Falsa.
Contraexemplo: √5 × √5 = 5.
b) → Falsa.
Contraexemplo: √5 + ( – √5) = 0.
c) → Falsa.
Contraexemplo: √10 e √15 estão entre 3 e 4 e são números irracionais.
e) → Falsa.
Contraexemplo: – 5 – ( – 7) = – 5 + 7 = – 2.
Considere a expressão numérica a seguir.
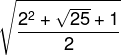
Sobre o resultado da expressão, podemos afirmar que:
A) é um número racional, mas não é inteiro.
B) é um número inteiro, mas não é natural.
C) é um número natural.
D) é um número irracional.
E) é um número real e racional.
Alternativa D.
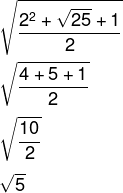
Sabemos que √5 é uma dízima não periódica, logo um número irracional.
(PUC-RS 2015) Em nossos trabalhos com matemática, mantemos um contato permanente com o conjunto ℝ dos números reais, que possui como subconjuntos o conjunto ℕ dos números naturais, o conjunto ℤ dos números inteiros, o ℚ dos números racionais e o dos números irracionais I. O conjunto dos números reais também pode ser identificado por:
A) ℕ ∪ ℤ
B) ℕ ∪ ℚ
C) ℤ ∪ ℚ
D) ℤ ∪ I
E) ℚ ∪ I
Alternativa E. O conjunto dos números reais é a união dos racionais com os irracionais.
