Exercícios sobre números reais

Sobre os números reais, podemos afirmar que:

I. Todo número racional é um número real.

II. Nem todo número irracional é um número real.

III. Todo número natural é um número real.

Marque a alternativa correta:

A) Somente a afirmativa I é falsa.

B) Somente a afirmativa II é falsa.

C) Somente a afirmativa III é falsa.

D) Todas as afirmativas são verdadeiras.

O número 3,141414... é:

A) Uma dízima periódica que pertence ao conjunto dos números irracionais.

B) Uma dízima não periódica que pertence ao conjunto dos números irracionais.

C) Uma dízima periódica que pertence ao conjunto dos números racionais.

D) Uma dízima não periódica que pertence ao conjunto dos números irracionais.

E) Uma dízima periódica que não pertence ao conjunto dos números reais.

Considerando m e n como elementos do conjunto dos números reais, analise a propriedade a seguir:

I. m + n = n + m

II. m ⋅ n = n ⋅ m

A propriedade demonstrada nas afirmativas I e II é conhecida como:

A) Propriedade distributiva

B) Propriedade associativa

C) Propriedade de Pitágoras

D) Propriedade comutativa

E) Fechamento para a soma e para o produto

Durante a resolução de problemas envolvendo o teorema de Pitágoras, Manoel realizou a seguinte operação:

\(x²=1^2+1^2\)

\(x^2=1+1\)

\(x^2=2\)

\(x=\sqrt2\)

Podemos classificar o número encontrado como resposta como:

A) um número real, natural e não inteiro.

B) um número real, inteiro e não racional.

C) um número real, racional e não inteiro.

D) um número real e irracional.

E) um número primo.

Sobre o conjunto dos números reais, julgue as afirmativas a seguir:

I. Existe um elemento neutro para a adição de dois números reais.

II. Existe um elemento neutro para a multiplicação de dois números reais.

III. Esse elemento neutro tanto para a adição quanto para a multiplicação é o 0.

Marque a alternativa correta:

A) Somente a afirmativa I é falsa.

B) Somente a afirmativa II é falsa.

C) Somente a afirmativa III é falsa.

D) Todas as afirmativas são verdadeiras.

Ao longo da história, surgiram vários conjuntos numéricos, e cada um deles foi criado para atender aos anseios da humanidade naquele instante. Sobre os conjuntos numéricos, podemos afirmar que:

A) o conjunto dos números reais está contido no conjunto dos números naturais.

B) o conjunto dos números reais está contido no conjunto dos números racionais.

C) o conjunto dos números reais contém o conjunto dos números complexos.

D) o conjunto dos números reais é a união dos conjuntos dos números racionais e irracionais.

E) o conjunto dos números reais é composto por todos os números que não podem ser representados como uma fração.

Sobre os conjuntos numéricos, julgue as afirmativas a seguir:

I. O conjunto dos números inteiros contém todos os números negativos.

II. Todo número racional é também um número irracional.

III. Para ser real, basta que um número seja irracional ou racional.

Marque a alternativa correta:

A) Somente I é verdadeira.

B) Somente II é verdadeira.

C) Somente III é verdadeira.

D) Todas são falsas.

Ao calcular o valor da expressão \(\frac{\sqrt2\ \cdot\ \sqrt18}{2-5}\), encontramos um número:

A) natural.

B) inteiro.

C) irracional.

D) racional, mas não inteiro.

(Copeve Ufal 2015) Dadas as afirmativas quanto aos conjuntos numéricos

I. A união do conjunto dos números inteiros com o conjunto dos números reais é igual ao conjunto dos números reais.

II. A interseção entre os conjuntos dos números reais, naturais e inteiros é igual ao conjunto dos números naturais.

III. A diferença entre o conjunto dos inteiros e o conjunto dos naturais é o conjunto vazio.

verifica-se que está(ão) correta(s)

A) I, apenas.

B) III, apenas.

C) I e II, apenas.

D) II e III, apenas.

E) I, II e III.

(Instituto Unique 2022) Leia o texto a seguir:

Segundo a história, o matemático Arquimedes de Saracusa, que viveu no século 3 a.C., teria sido o primeiro a calcular o π (pi). Depois dele, as ciências entraram em um período estranho e pouco ativo. Foi só por volta do ano 1.000 de nossa era que os árabes começaram novamente a estudar os cálculos matemáticos com mais afinco. Nessa época, os estudos indo-arábicos começaram a se espalhar por toda a Europa, causando impacto na Aritmética e na Trigonometria, por exemplo. O número π foi um dos afetados: em 1665, Sir Isaac Newton registrou 16 dígitos depois da vírgula — algo que até hoje não chegou a um fim.

Disponível em: <http://www.megacurioso.com.br/matematica-e-estatistica/102113-no-dia-do-pi-descubra-por-que-o-numero-3-14-tem-esse-nome>. Acessado em 22/11/2018.

Com base no texto e em seus conhecimentos, podemos dizer que o número π é:

A) um número decimal, portanto racional.

B) uma dízima periódica, portanto racional.

C) uma dízima periódica, portanto real.

D) irracional, portanto real.

(Fundatec 2021) Acerca dos conjuntos numéricos e suas características, analise os seguintes números:

83 e \(\sqrt3\)

Sobre eles, assinale a alternativa correta:

A) 83 é um número inteiro, irracional e real.

B) \(\sqrt3\) é um número racional e real.

C) 83 é um número natural, irracional e real.

D) \(\sqrt3\) é um número irracional e real.

E) Ambos os números são naturais, inteiros, racionais e reais.

(Unilavras 2018) Se a figura, em que (2 ⊂ 4) ⊂ 1 e 3 ⊂ 1, representasse conjuntos numéricos, os triângulos 1, 2, 3 e 4 seriam, nessa ordem, os conjuntos

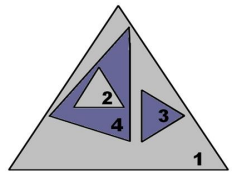
A) reais, naturais, racionais, irracionais.

B) reais, inteiros, irracionais, racionais.

C) reais, naturais, inteiros, irracionais.

D) reais, racionais, inteiros, naturais.