Exercícios sobre operações com números complexos
Para resolver estes exercícios sobre operações com números complexos, é necessário analisar cuidadosamente suas partes real e imaginária.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Considere os seguintes números complexos z1 = 10 + 2i, z2 = 5 – 3i e z3 = – 9 + 5i e calcule a sua soma:
Vamos organizar os números complexos para somar de forma separada as partes reais e as partes imaginárias:
z1 + z2 + z3
(10 + 2i) + (5 – 3i) + (– 9 + 5i)
(10 + 5 – 9) + (2 – 3 + 5)i
6 + 4 i
Portanto, a soma dos complexos z1, z2 e z3 é igual a 6 + 4i.
-
Questão 2
Calcule a subtração destes dois números complexos: z1 = 12 – 3i e z2 = 15 + 2i.
Organizando os números complexos para efetuar a subtração entre eles:
z1 – z2
(12 – 3i ) – (15 + 2i)
(12 – 15) + (– 3 – 2)i
– 3 – 5i
A diferença dos complexos z1 e z2 é igual a – 3 – 5i.
-
Questão 3
(Unesp-SP) Se z = (2 + i) ∙ (1 + i) ∙ i, então z, o conjugado de z, será dado por:
Primeiramente vamos fazer as multiplicações necessárias em z:
z = (2 + i) ∙ (1 + i) ∙ i
z = (2 + 2i + i + i²) ∙ i
z = (2 + 3i – 1) ∙ i
z = (1 + 3i) ∙ i
z = i + 3i²
z = i + 3 ∙ (– 1)
z = – 3 + i
Agora que encontramos a forma mais simples de z, basta alterar o sinal da parte imaginária para termos seu conjugado:
z = – 3 – i
Portanto, a alternativa correta é a letra a.
-
Questão 4
(UFSCar-SP) Sejam x, y R e z = x + yi um número complexo.
a) Realizando a multiplicação pedida, temos:
(x + yi) ∙ (1 + i)
x + yi + xi + yi²
x + yi + xi + y(– 1)
(x – y) + (x + y)∙i
O produto (x + yi) ∙ (1 + i) equivale a (x – y) + (x + y)∙i.
b) Podemos considerar que 2 escrito na forma complexa equivale a 2 + 0i. Como já determinamos o produto (x – y) + (x + y)∙i, basta que na equação abaixo igualemos as partes reais e também as partes imaginárias:
(x – y) + (x + y)∙i = 2 + 0i
Parte Real
x – y = 2
Parte Imaginária
x + y = 0
Podemos montar um sistema com as equações encontradas e resolvê-lo pelo método da adição:
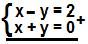
2x = 2
x = 2
2
x = 1
Substituindo o valor encontrado de x na equação da parte imaginária, temos:
x + y = 0
1 + y = 0
y = – 1
Portanto, para que tenhamos (x + yi) ∙ (1 + i) = 2, é necessário que x = 1 e y = – 1.