Exercícios sobre os quatro erros mais cometidos em trigonometria básica
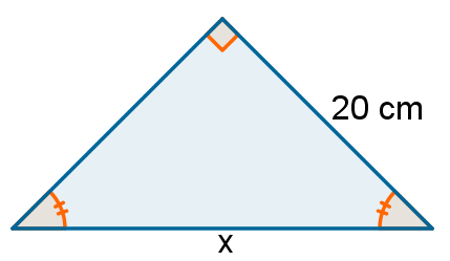
O triângulo a seguir é retângulo e, como demarcado na figura, os seus ângulos agudos são congruentes. Qual é o valor de x?
a) 20√2
b) 30√2
c) 40√2
d) 20√3
e) 40√3
Se os ângulos são iguais, cada um mede 45°. Usando a razão seno, temos:
sen45° = 20
x
Lembrando que sen45° = √2/2, temos:
√2 = 20
2 x
x·√2 = 2·20
x = 40
√2
Racionalizando, temos:
x = 40√2 = 40√2 = 20√2
√2√2 2
Alternativa A
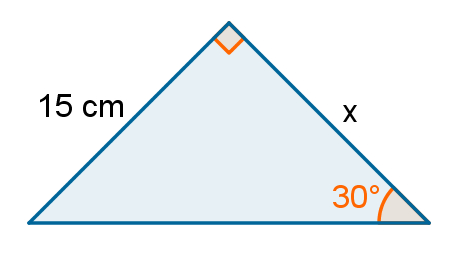
O triângulo a seguir é retângulo, e um de seus ângulos agudos mede 30°. Qual é o valor de x?
a) 15√3
b) 10√3
c) 5√3
d) 15√2
e) 5√2
Observe que x e 15 cm são as medidas dos catetos desse triângulo. Dessa maneira, devemos usar a razão tangente para encontrar a medida de x.
tg30° = 15
x
Sabendo que tg30° = √3, temos:
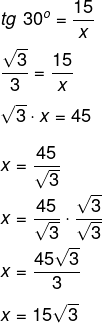
Alternativa A
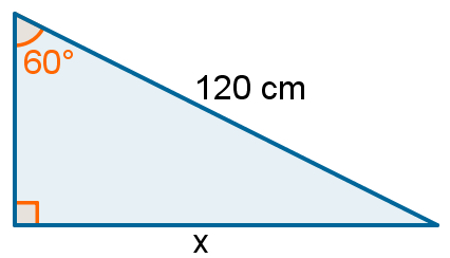
Na figura a seguir, há um triângulo retângulo com um de seus ângulos agudos medindo 60°. Determine o comprimento do lado representado pela letra x, em centímetros.
a) 120√2 cm
b) 120√3 cm
c) 60 cm
d) 60√2 cm
e) 60√3 cm
Nesse exercício, basta usar a razão seno para o ângulo de 60°, sabendo que:
sen60° = √3
2
Observe:
sen60° = x
120
√3 = x
2 120
2x = 120√3
x = 120√3
2
x = 60√3 cm
Alternativa E
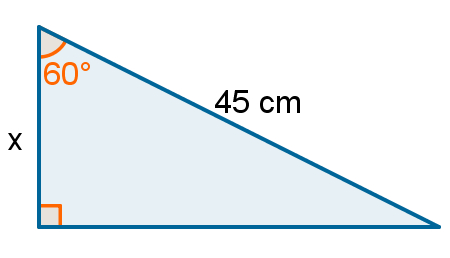
Na imagem a seguir, x é a medida de um dos lados de um triângulo retângulo. Dados os valores de um de seus ângulos e de outro de seus lados, determine o valor de x.
a) 45 cm
b) 40,5 cm
c) 25 cm
d) 22,5 cm
e) 7 cm
Para resolver esse problema, devemos usar a razão cosseno, lembrando-se de que:
cos60° = 1
2
Portanto:
cos60° = x
45
1 = x
2 45
2x = 45
x= 45
2
x = 22,5 cm
Alternativa D
