Exercícios sobre paralelepípedo
Um sólido geométrico é classificado como paralelepípedo quando:
A) ele possui faces opostas paralelas.
B) ele é um prisma, independentemente da sua base.
C) ele possui uma face no formato de um paralelogramo.
D) ele possui todas as faces formadas por paralelogramos.
Alternativa D
Para que um sólido geométrico seja considerado um paralelepípedo, é necessário que todas as suas faces sejam paralelogramos.
Um recipiente de madeira será construído no formato de um paralelepípedo retangular, com 7 metros de largura, 4 metros de comprimento e 2 metros de altura. Sabendo que serão gastos R$ 32,00 por metro quadrado desse recipiente, o valor necessário para a sua fabricação será de:
A) R$ 3200,00
B) R$ 3500,00
C) R$ 5000,00
D) R$ 6400,00
E) R$ 7200,00
Alternativa A
Calculando a área total:
\(A_T=2\cdot\left(7\cdot4+7\cdot2+4\cdot2\right)\)
\(A_T=2\cdot\left(28+14+8\right)\)
\(A_T=2\cdot50\)
\(A_T=100\)
Sabendo que a área total é de 100 m², o valor gasto será de:
100⋅32=R$ 3200,00
A diagonal de um paralelepípedo retângulo é de 12,5 cm. Considerando que a sua largura é de 6 cm e que o seu comprimento é de 8 cm, qual é a medida da altura?
A) 7,0 cm
B) 7,5 cm
C) 8,0 cm
D) 8,5 cm
E) 9,5 cm
Alternativa B
Se a diagonal é de 12,5 cm, temos que:
\(d²=a²+b²+c²\)
\(12,5²=62+82+c2\)
\(156,25=36+64+c^2\)
\(156,25=100+c^2\)
\(156,26-100=c^2\)
\(56,26=c^2\)
\(c=\sqrt{56,26}\)
\(c=7,5 cm\)
Um paralelepípedo possui base quadrada com lados medindo 6 cm e altura igual a 7 cm. Nessas condições, a medida da diagonal desse paralelepípedo é igual a:
A) 8 cm
B) 9 cm
C) 10 cm
D) 11 cm
E) 12 cm
Alternativa D
Calculando a diagonal:
\(d=\sqrt{a^2+b^2+c^2}\)
\(d=\sqrt{6^2+6^2+7^2}\)
\(d=\sqrt{36+36+49}\)
\(d=\sqrt{121}\)
\(d=11\ cm\)
Uma caixa possui as seguintes dimensões:
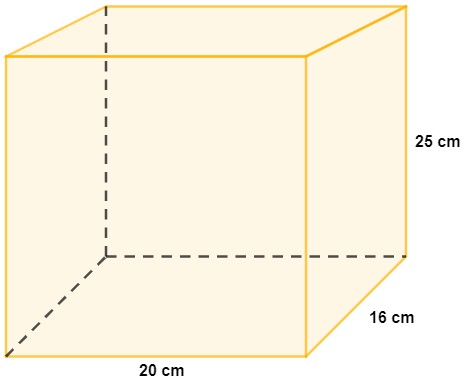
3/4 da caixa estão cheios, então qual é o volume ainda desocupado?
A) 2 000 cm³
B) 5 000 cm³
C) 6 000 cm³
D) 8 000 cm³
E) 12 000 cm³
Alternativa A
Para calcular o volume, basta fazer a multiplicação das três dimensões do paralelepípedo:
\(V=20\cdot16\cdot25\)
\(V=8\ 000\ cm^3\)
Agora calcularemos 3/4 da caixa:
\(8\ 000\cdot\frac{3}{4}=\frac{24\ 000}{4}=6\ 000\ cm^3\)
Se 6000 cm³ estão ocupados, resta um total de:
\(8\ 000-6\ 000=2\ 000\ cm^3\)
No paralelepípedo a seguir, foi traçado o segmento LM que vai de um vértice a outro.
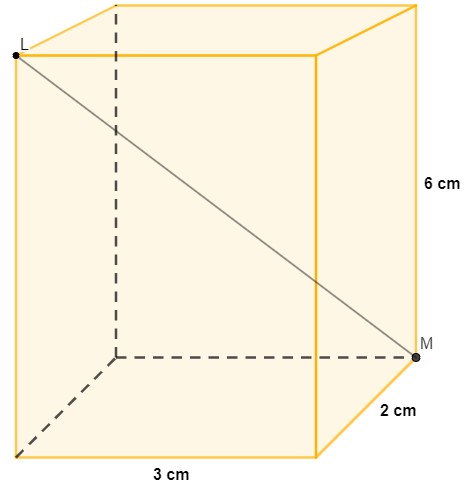
De acordo com as medidas desse paralelogramo, o comprimento do segmento LM é de:
A) 5 cm
B) 6 cm
C) 7 cm
D) 8 cm
E) 9 cm
Alternativa C
Calculando o comprimento da diagonal do paralelepípedo:
\(d^2=3^2+2^2+6^2\)
\(d^2=9+4+36\)
\(d^2=49\)
\(d=\sqrt{49}\)
\(d=7\ cm\)
Um tanque com a forma de um paralelepípedo retângulo de dimensões de 300 dm, 4000 mm e 200 cm está com 75% do seu volume ocupado com água. Quantos litros de água faltam para encher completamente o tanque?
A) 80.000
B) 160.000
C) 120.000
D) 60.000
Alternativa D
Para calcular o volume, converteremos todas as medidas em cm:
\(300 dm = 3000 cm\)
\(4000 mm = 400 cm\)
Logo, temos que:
\(V=200\cdot3000\cdot400\)
\(V9=240.000.000\ cm³\)
Para converter cm³ em litros, basta dividir por 1000:
\(240.000.000∶1000=240.000\)
\(V=240.000\ l\)
Se 75% está ocupado, resta 25%:
\(0,25\cdot240.000=60.000\ l\ \)
Assim, restam 60.000 litros a serem preenchidos.
Um paralelepípedo retângulo possui 8 cm de largura, 12 cm de comprimento e 18 cm de altura. Podemos afirmar que o volume desse sólido geométrico é igual a:
A) 1004 cm³
B) 1128 cm³
C) 1276 cm³
D) 1582 cm³
E) 1728 cm³
Alternativa E
Para calcular o volume do paralelepípedo retângulo, basta multiplicar as suas três dimensões:
\(V=8\cdot12\cdot18\)
\(V=1728\ cm^3\)
(Enem 2010) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura. Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a
A) 5 cm
B) 6 cm
C) 12 cm
D) 24 cm
E) 25 cm
Alternativa B
Primeiramente, calcularemos o volume da barra que possui formato de um paralelepípedo:
\(V=3\cdot18\cdot4\)
\(V=216\)
Como o volume da barra que possui formato de cubo é o mesmo, para calcular a aresta do cubo temos que:
\(a^3=216\)
\(a=\sqrt[3]{216}\)
\(a=6\)
Podemos concluir que a aresta do cubo deve ter 6 cm.
(Covest/Copset 2015 - UFPE) A empresa gestora de um porto precisa construir um novo cais. A laje de betão para o cais, na forma de um paralelepípedo retângulo, precisa ter 75 m de comprimento, 60 m de largura e 0,3 m de espessura. Se a carga de um caminhão cheio de betão é de 25 m³, quantos caminhões carregados de betão serão necessários para construir a laje? Informação: o volume de um paralelepípedo retângulo é dado pelo produto das medidas de seu comprimento, largura e espessura.
A) 50
B) 51
C) 52
D) 53
E) 54
Alternativa E
Calculando o volume da lage VL:
\(V_L=75\cdot60\cdot0,3=1350\)
Já a carga do caminhão é de 25 m³. Calculando a divisão para saber a quantidade de caminhões:
\(1350∶25=54\ \)
(Enem 2011) A siderúrgica Metal Nobre produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com:
O produto das três dimensões indicadas na peça resultaria na medida da grandeza
A) massa.
B) volume.
C) superfície.
D) capacidade.
E) comprimento.
Alternativa B
Quando multiplicamos as três dimensões, calculamos o volume, pois o objeto é maciço, e o produto das suas dimensões resulta no volume desse sólido geométrico.
Marcelo decidiu comprar um container para abrigar o material da sua construção. Ele comprou um recipiente usado e decidiu refazer a pintura dos 6 lados desse container para mantê-lo conservado.
Analisando as dimensões do container, conclui-se que a área que será pintada é de:
A) 72,48 m²
B) 60,28 m²
C) 58,40 m²
D) 54,22 m²
E) 31,04 m²
Alternativa A
Calculando a área do container:
\(A=2\left(2,4\cdot6+2,4\cdot2,6+6\cdot2,6\right)\)
\(A=2\left(14,4+6,24+15,6\right)\)
\(A=2\cdot36,24\)
\(A=72,48\ m^2\)
