Leia conteúdos de todas as disciplinas
Exercícios sobre perímetro do quadrado
Um terreno possui formato de quadrado, com lado medindo 12 metros. Qual é o valor do perímetro desse terreno?
A) 24 m
B) 36 m
C) 42 m
D) 48 m
E) 54 m
Alternativa D.
O perímetro do quadrado é igual a quatro vezes a medida do seu lado, então:
P = 4 ⋅12
P = 48 m
Ao realizar um projeto de um carro, o engenheiro percebeu que acabou se esquecendo de anotar a medida do lado de uma peça que possui formato quadrado. Ele sabe que essa peça possui perímetro igual a 9 cm, então a medida do lado dessa peça é de:
A) 4,50 cm.
B) 3,00 cm.
C) 2,75 cm.
D) 2,25 cm.
E) 1,75 cm.
Alternativa D.
O perímetro é a soma dos quatro lados, logo:
P = 9
Então, temos que:
4L = 9
L=94
L = 2,25
A medida do lado é de 2,25 cm.
Um campo de futebol society tem formato quadrado com 30 metros de lado. Qual é o perímetro desse campo?
A) 60 m
B) 90 m
C) 120 m
D) 150 m
E) 180 m
Alternativa C.
Sabemos que o quadrado possui quatro lados iguais, então o seu perímetro será de:
P = 4 ⋅ 30
P = 120 m
Heitor quer fazer uma moldura quadrada para uma foto de 25 cm de lado. Qual o perímetro dessa moldura?
A) 50 cm.
B) 75 cm.
C) 100 cm.
D) 125 cm.
E) 150 cm.
Alternativa C.
Para calcular o perímetro do quadrado, basta multiplicar a medida do lado por 4:
P = 4 ⋅ 25
P = 100 cm
Uma empresa fabrica embalagens que são quadradas e precisa determinar o tamanho do lado de uma embalagem. Sabe-se que o perímetro da embalagem é 48 cm. Qual é o comprimento de cada lado dessa embalagem?
A) 10 cm.
B) 12 cm.
C) 14 cm.
D) 16 cm.
E) 18 cm.
Alternativa B.
Sabemos que, se o perímetro é 48 e a figura é um quadrado, ou seja, possui os quatro lados iguais, então basta igualar o perímetro a 48:
P = 48
4L = 48
L=484
L = 12 cm
Uma escola separou uma área para construir a sua horta educativa. Sabendo que essa área será cercada com arame, utilizando 4 fios por lado, a área escolhida possui formato de um quadrado com 3 metros de lado. Nessas condições, qual é a quantidade mínima em metros de fio necessária para cercar essa área?
A) 12 metros.
B) 24 metros.
C) 36 metros.
D) 48 metros.
E) 60 metros.
Alternativa D.
Sabemos que o perímetro será de:
P = 4 ⋅ 3 = 12 m
Se serão usados quatro fios de arame, então a quantidade de arame utilizada será de:
P = 4 ⋅ 12
P = 48 m
Uma escola construiu uma miniquadra quadrada para recreação. O perímetro da quadra é 80 metros. Então a medida de cada lado da miniquadra é de:
A) 10 m
B) 20 m
C) 30 m
D) 40 m
E) 50 m
Alternativa B.
Se o perímetro é de 80 metros, então temos que:
P= 80
Mas como os quatro lados do quadrado são sempre congruentes, então temos que:
4L = 80
L=804
L = 20 m
O lado de um quadrado é desconhecido, mas a equação que representa a medida desse lado em função do valor de x é 2x + 1. Se a medida do perímetro desse quadrado é de 40 cm, então o valor de x é:
A) 2,0
B) 4,5
C) 6,0
D) 8,5
E) 10,0
Alternativa B.
Sabemos que o perímetro é de 40 cm, L = 2x + 1, então temos que:
P = 4L
40 = 4 (2x + 1)
40 = 8x + 4
40 - 4 = 8x
36 = 8x
368=x
4,5 = x
Assim:
x = 4,5
A área de um terreno é de 25 m2. Sabendo que ele possui formato de um quadrado, então a medida do seu perímetro é de:
A) 5 m.
B) 10 m.
C) 15 m.
D) 20 m.
E) 25 m.
Alternativa D.
A área do quadrado é igual à medida do quadrado do seu lado, logo:
A = l2
Sabemos também que:
A = 25
Então temos que:
l2 = 25
l = √25
l = 5
Se o lado mede 5 m, então o perímetro desse terreno é igual a quatro vezes a medida do lado:
P = 4 ⋅ 5
P = 20 m
O perímetro do quadrado a seguir mede:
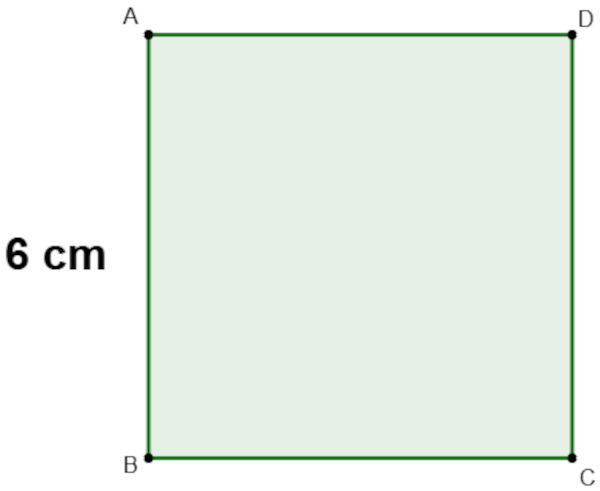
A) 6 cm.
B) 12 cm.
C) 18 cm.
D) 20 cm.
E) 24 cm.
Alternativa E.
Sabendo que o lado mede 6 cm, então a medida do perímetro é de:
P = 4 ⋅ 6
P = 24 cm
O perímetro de um quadrado é dado pela equação P = 8x + 4. Sabendo que o lado desse quadrado mede 7 cm, então o valor de x é:
A) 7.
B) 6.
C) 5.
D) 4.
E) 3.
Alternativa E.
Sabendo que o lado mede 7, então o perímetro desse quadrado é igual a 4 vezes a medida do lado:
P = 4 ⋅ 7
P = 28
Se o perímetro mede 28, então o valor de x será:
8x + 4 = 28
8x = 28 - 4
8x = 24
x=248
x = 3
Um quadrado A possui lado medindo L cm. Se a medida do lado B é igual ao dobro da medida do quadrado A, então o perímetro do novo quadrado será:
A) o mesmo perímetro do quadrado A.
B) o dobro do perímetro do quadrado A.
C) o triplo do perímetro do quadrado A.
D) quatro vezes o perímetro do quadrado A.
Alternativa B.
Seja L a medida do lado, sabemos que o dobro de L será 2L, então, analisando o perímetro, temos que:
P1 = 4L
Após dobrar o lado, temos que:
P2 = 4 ⋅ (2L)
L2 = 8L
Então, sabemos que 8L é o dobro de 4L, logo o perímetro também será o dobro.
Ferramentas
