Exercícios sobre poliedros
Os sólidos de Platão são conhecidos como os únicos poliedros regulares, ou seja, todas as faces são iguais. Dos poliedros a seguir, são considerados sólidos de Platão, exceto:
A) cubo.
B) dodecaedro.
C) tetraedro.
D) paralelepípedo.
E) icosaedro.
Alternativa D. Os paralelepípedos nem sempre são sólidos de Platão, pois as suas faces não são todas iguais, exceto quando ele é um hexaedro regular. Assim sendo, não podemos afirmar que todo paralelepípedo é um sólido de Platão.
Um poliedro convexo possui 20 faces e 12 vértices, então o número de arestas desse poliedro é:
A) 20.
B) 24.
C) 28.
D) 30.
E) 32.
Alternativa D.
Sabemos que ele é convexo, logo vale a relação de Euler:
V + F = A + 2
12 + 20 = A + 2
32 = A + 2
A = 32 – 2
A = 30
(Fuvest) O número de faces triangulares de uma pirâmide é 11. Pode-se, então, afirmar que essa pirâmide possui:
A) 33 vértices e 22 arestas.
B) 12 vértices e 11 arestas.
C) 22 vértices e 11 arestas.
D) 11 vértices e 22 arestas.
E) 12 vértices e 22 arestas.
Alternativa E. A pirâmide possui todas as faces laterias no formato de triângulos. Além dessas 11 faces triangulares, há somente mais 1 face, a face da base, que é formada por um polígono de 11 lados e 11 vértices, já que há 11 faces triangulares. Além dos 11 vértices da base, esse polígono possui também o chamado vértice da pirâmide. Assim sendo, esse poliedro possui 12 vértices. Pela relação de Euler, temos que:
V + F = A + 2
12 + 12 = A + 2
24 = A + 2
A = 24 – 2
A = 22
Portanto, 12 vértices e 22 arestas.
Analise o sólido geométrico a seguir:
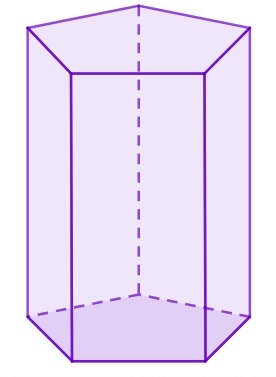
Podemos afirmar que:
(I) esse sólido geométrico possui o total de 10 arestas.
(II) esse sólido geométrico é composto por 5 retângulos e 2 pentágonos.
(III) esse sólido geométrico é um poliedro.
Marque a alternativa correta.
A) Somente I é falsa
B) Somente II é falsa
C) Somente III é falsa
D) Somente I e II são falsas
E) Somente I e III são falsas
Alternativa A.
(I) Falsa, pois ele possui um total de 15 arestas.
(II) Verdadeira.
(III) Verdadeira.
Considere as afirmações a seguir sobre poliedros.
I → O cilindro é um poliedro, pois suas faces são formadas por círculos.
II → A pirâmide é um poliedro, pois sua base é um polígono e as suas faces laterais são triângulos.
III → O trapézio é um poliedro, pois ele possui lados formados por polígonos e é fechado.
Marque a alternativa correta.
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas II e III são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Alternativa B.
I → Falsa, pois o cilindro é um corpo redondo, e não um poliedro.
II → Verdadeira.
III → Falsa, pois o trapézio é um objeto bidimensional, logo ele é um polígono, e não um poliedro.
(Enem 2017) Uma rede hoteleira dispõe de cabanas simples na ilha de Gotland, na Suécia, conforme Figura 1. A estrutura de sustentação de cada uma dessas cabanas está representada na Figura 2. A ideia é permitir ao hóspede uma estada livre de tecnologia, mas conectada com a natureza.
A forma geométrica da superfície cujas arestas estão representadas na Figura 2 é
A) tetraedro.
B) pirâmide retangular.
C) tronco de pirâmide retangular.
D) prisma quadrangular reto.
E) prisma triangular reto.
Um poliedro pode ser classificado como convexo ou côncavo, dependendo do seu formato. Veja alguns poliedros.
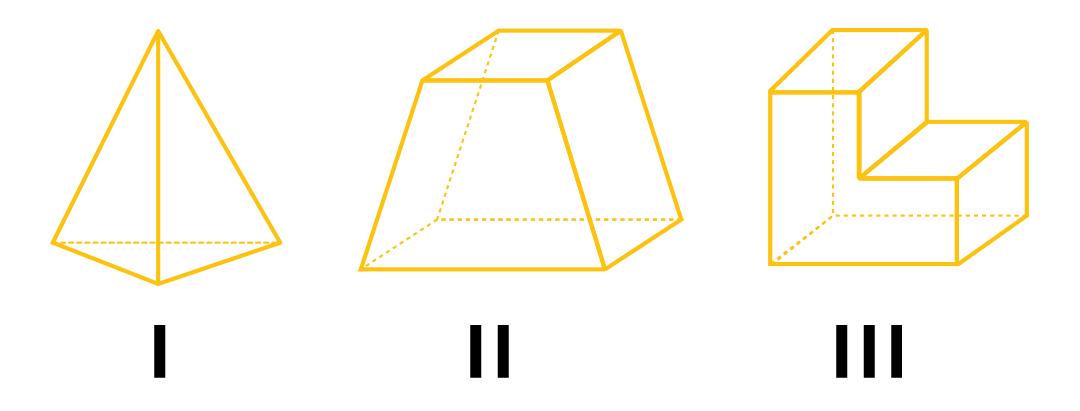
A) Convexo, convexo e côncavo.
B) Côncavo, convexo e côncavo.
C) Convexo, côncavo e convexo.
D) Convexo, Convexo e côncavo.
E) Côncavo, côncavo e convexo.
Alternativa D. Um poliedro é côncavo quando, dados dois pontos pertencentes ao poliedro, o segmento que liga esses dois pontos não pertence ao poliedro, caso contrário ele é convexo. O único poliedro que satisfaz a definição para ser côncavo é o III, então:
I → convexo
II → convexo
III → côncavo
Um garimpeiro encontrou uma pedra preciosa que possui o formato igual ao do poliedro a seguir:
Analisando o poliedro a seguir, podemos afirmar que a soma do número de faces, vértices e arestas é igual a:
A) 26.
B) 25.
C) 24.
D) 23.
E) 22.
Alternativa A.
Primeiro vamos contar o número de vértices, arestas e faces na imagem.
A = 12
F = 8
V = 6
Agora, basta realizar a soma:
A + F + V = 12 + 8 + 6 = 26
(Cesgranrio) Um poliedro convexo é formado por 4 faces triangulares, 2 faces quadrangulares e 1 face hexagonal. O número de vértices desse poliedro é de:
A) 6.
B) 7.
C) 8.
D) 9.
E) 10.
Alternativa C.
Calculando o total de arestas, temos que:
4 faces triangulares → 4 · 3
2 faces quadrangulares → 2 · 4
1 face hexagonal → 6
Sabemos que o lado dos polígonos corresponde às arestas do poliedro. Além disso, a aresta é o encontro de duas faces, logo, para encontrar o número de arestas, vamos calcular o total de arestas e dividir por dois, pois elas pertencem a duas faces simultaneamente.
A = (4 · 3 + 2 · 4 + 6 ) : 2
A = (12 + 8 + 6) : 2
A = 26 : 2
A = 13
O total de faces é 4 + 2 + 1 = 7.
Pela relação de Euler, temos que
V + F = A + 2
V + 7 = 13 + 2
V + 7 = 15
V = 15 – 7
V = 8
(Unirio) Um geólogo encontrou, numa de suas explorações, um cristal de rocha no formato de um poliedro, que satisfaz a relação de Euler, de 60 faces triangulares. O número de vértices desse cristal é igual a:
A) 35.
B) 34.
C) 33.
D) 32.
E) 31.
Alternativa D.
Se ele possui 60 faces triangulares, sabemos que cada face tem 3 arestas; porém, a aresta é o encontro de duas faces, então, para calcular a quantidade de arestas, vamos multiplicar o número de faces por 3 e dividir por 2.
60 · 3 : 2 = 90 arestas.
Agora, pela relação de Euler, temos que:
V + F = A + 2
V + 60 = 90 + 2
V = 92 – 60
V = 32
Considere os sólidos geométricos a seguir.
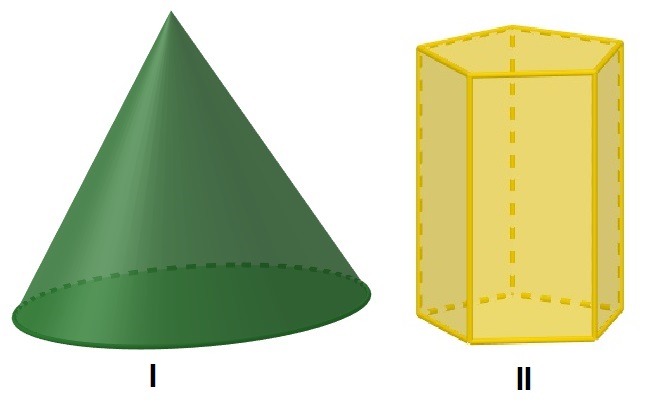
Podemos afirmar que:
A) somente I é um poliedro.
B) somente II é um poliedro.
C) ambos são poliedros.
D) nenhum deles é um poliedro.
E) ambos são polígonos.
Alternativa B. Analisando os sólidos geométricos, o I é um cone, que é um corpo redondo e não pode ser classificado como poliedro. Já o sólido geométrico II é um prisma de base pentagonal, que é um poliedro.
Marque a alternativa que possui somente poliedros.
A) Hexaedro, prisma de base triangular, cone.
B) Esfera, cilindro e tronco de cone.
C) Cubo, pirâmide de base quadrada e prisma.
D) Cubo, cone e cilindro.
E) Tronco da pirâmide, pirâmide e elipse.
Alternativa C.
O cubo, as pirâmides e os prismas são todos poliedros.
