Exercícios sobre Porcentagem

(Enem 2014) Uma ponte precisa ser dimensionada de forma que possa ter três pontos de sustentação. Sabe-se que a carga máxima suportada pela ponte será de 12 t. O ponto de sustentação central receberá 60% da carga da ponte, e o restante da carga será distribuído igualmente entre os outros dois pontos de sustentação.

No caso de carga máxima, as cargas recebidas pelos três pontos de sustentação serão, respectivamente:

A) 1,8 t; 8,4 t; 1,8 t.

B) 3,0 t; 6,0 t; 3,0 t.

C) 2,4 t; 7,2 t; 2,4 t.

D) 3,6 t; 4,8 t; 3,6 t.

E) 4,2 t; 3,6 t; 4,2 t.

(Enem 2014) Os vidros para veículos produzidos por certo fabricante têm transparências entre 70% e 90%, dependendo do lote fabricado. Isso significa que, quando um feixe luminoso incide no vidro, uma parte entre 70% e 90% da luz consegue atravessá-lo. Os veículos equipados com vidros desse fabricante terão instaladas, nos vidros das portas, películas protetoras cuja transparência, dependendo do lote fabricado, estará entre 50% e 70%. Considere que uma porcentagem P da intensidade da luz, proveniente de uma fonte externa, atravessa o vidro e a película.

De acordo com as informações, o intervalo das porcentagens que representam a variação total possível de P é:

A) [35;63].

B) [40;63].

C) [50;70].

D) [50;90].

E) [70;90].

(Cesgranrio 2010) Maria quer comprar uma bolsa que custa R$ 85,00 à vista. Como não tinha essa quantia no momento e não queria perder a oportunidade, aceitou a oferta da loja de pagar duas prestações de R$ 45,00, uma no ato da compra e outra um mês depois. A taxa de juros mensal que a loja estava cobrando nessa operação era de

A) 5,0%.

B) 5,9%.

C) 7,5%

D) 10,0%.

E) 12,5%.

Para atrair uma maior clientela, uma loja de móveis fez uma promoção oferecendo um desconto de 20% em alguns de seus produtos.

No gráfico, estão relacionadas as quantidades vendidas de cada um dos produtos, em um dia de promoção.

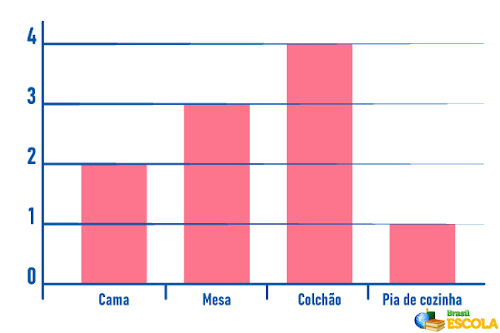
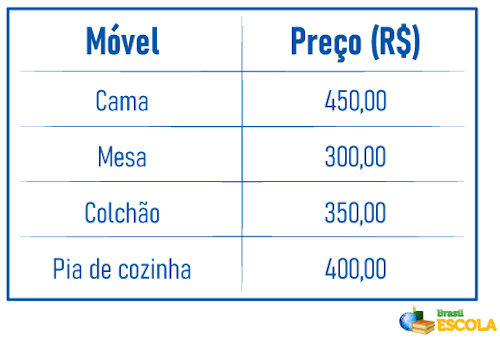
No quadro constam os preços de cada produto vendido já com desconto de 20% oferecido pela loja.

Qual foi o valor total de desconto, em reais, concedido pela loja com a venda desses produtos durante esse dia de promoção?

 A) 300,00

 B) 375,00

 C) 720,00

 D) 900,00

 E) 1125,00

No Colégio Aplicação, ao chegar ao ensino médio, os estudantes podem escolher um entre três idiomas (inglês, francês e espanhol) para aprofundar os seus conhecimentos. Sabendo que há  180 alunos no ensino médio e que 45 deles escolheram espanhol, 20% escolheram francês, então a porcentagem de estudantes que escolheram inglês foi de:

A) 55%.

B) 75%.

C) 25%.

D) 12,5%.

E) 30%.

Durante as eleições de síndico do condomínio, havia três candidatos. Sabendo que há 400 moradores, mas que apenas 16% compareceram a essa reunião e que, dos condôminos presentes, 62,5% votaram no candidato vencedor, o total de pessoas que votaram no candidato vencedor é de:

A) 30.

B) 35.

C) 40.

D) 45.

E) 50

Durante uma venda de apartamentos, as construtoras contrataram empresas especialistas em vendas de imóveis. Essa empresa cobra 5% por cada uma das unidades vendidas, e essa comissão é dividida entre a empresa, o corretor que fechou a venda e o gerente comercial do corretor. Sabendo que um apartamento foi vendido e que a empresa de vendas de imóveis recebeu R$ 17.150,00, o valor de venda desse apartamento foi de?

A) R$ 350.000,00.

B) R$343.000,00.

C) R$320.000,00.

D) R$374.000,00.

E) R$300.150,00.

Quando um devedor atrasa a conta, é bastante comum a cobrança de juros e multa pelo atraso. Uma conta de energia, que inicialmente custava R$ 250,00, foi paga com atraso de 3 meses. Na conta havia explicações referentes ao cálculo dos juros e da multa. A multa é de 5% e os juros são de 1% a cada mês. O valor total pago por essa conta foi de:

A) R$ 257,50.

B) R$  262,50.

C) R$ 250,00.

D) R$ 265,00.

E) R$ 270,00.

Em abril o valor de uma cesta de chocolate era de R$ 135,00, porém, devido à proximidade do Dia dos Namorados, no início do mês de maio essa cesta teve um aumento de 20%.  No mês de junho, houve uma nova mudança no valor: uma redução de 20% em relação ao mês de maio. Ao comparar o valor da cesta no decorrer dos meses, podemos afirmar que:

A) o valor da cesta em abril e junho é o mesmo.

B) o valor da cesta em abril é maior do que o valor de junho.

C) o valor da cesta em junho é maior do que o valor da cesta em abril.

D) o valor da cesta em maio é o mesmo que de junho.

No ano de 2020, um dos problemas foi o alto índice de queimadas no Pantanal, atingindo os maiores índices de focos de incêndio da história. Dados dos institutos responsáveis apontam que 15% do bioma foi consumido pelas chamas, uma área equivalente a 2,2 milhões de hectares. Podemos afirmar que o território do Pantanal em hectares é de:

A) 12 milhões.

B) 12,5 milhões.

C) 13 milhões.

D) 13,3 milhões.

E) 14,7 milhões.

Durante as queimadas no Pantanal em 2020, até meados de setembro, os satélites da região registraram, para o Instituto Nacional de Pesquisas Espaciais (Inpe), 12.700 focos ativos de incêndio, que representam dezenas de frentes descontroladas de queimadas. São os maiores números já registrados. Suponha que, após o mês de setembro, houve ações para reduzir esse número por meio de trabalho voluntário, o que gerou a redução de 35% das queimadas. Então, o total de focos restantes é:

A) 8.255.

B) 4.445.

C) 6.985.

D) 9.543.

E) 7.366.

(Enem) A Organização Mundial da Saúde (OMS) recomenda que o consumo diário de sal de cozinha não exceda 5 g. Sabe-se que o sal de cozinha é composto por 40% de sódio e 60% de cloro.

Disponível em: http://portal.saude.gov.br. Acesso em: 29 fev. 2012 (adaptado).

Qual é a quantidade máxima de sódio proveniente do sal de cozinha, recomendada pela OMS, que uma pessoa pode ingerir por dia?

A) 1250 mg

B) 2000 mg

C) 3000 mg

D) 5000 mg

E) 12.500 mg

(IFG Técnico Integrado) Uma pessoa aplicou R$ 6.000,00 a juros simples à taxa de 36% ao ano. Ao final de 84 dias, ela recebeu um montante no valor de:

A) R$ 6.504,00

B) R$ 6.503,00

C) R$ 6.502,00

D) R$ 6.501,00

E) R$ 6.499,00

(IFG Técnico Integrado) As dimensões de uma caixa d’água em forma de paralelepípedo são 3 m de comprimento, 2 m de largura e 1,20 m de altura. Sabendo-se que a caixa d’água está apenas com 75% de sua capacidade, quantos litros faltam para enchê-la totalmente?

A) 1.780

B) 1.790

C) 1.800

D) 1.760

E) 1.770

(IFG Técnico Integrado) Um capital de R$ 36.000,00 foi aplicado no sistema de juros simples no período de 6 meses e resultou em um montante de R$ 38.160,00. Logo, a taxa mensal de juros que rendeu esse investimento equivale a:

A) 1,5%

B) 0,7%

C) 2%

D) 0,5%

E) 1%

(IFG Técnico Integrado) Na tabela abaixo, podemos identificar o número de matrículas de todos os alunos do início do ano letivo de 2018, em um dos quatorze campus do Instituto Federal de Goiás, e os turnos escolhidos, de acordo com os cursos.

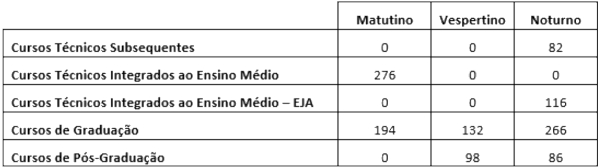
Considerando o exposto acima e que todos os alunos optaram por apenas um turno do seu curso, é correto afirmar que:

A) 44% dos alunos matriculados estudam no turno noturno.

B) 38% dos alunos matriculados estudam no turno matutino.

C) 15% dos alunos matriculados são dos cursos de pós-graduação.

D) Pouco mais da metade dos alunos estão matriculados em cursos técnicos.

(IFG – Técnico Integrado) Num posto de combustível em Goiânia, observou-se a mudança do preço do litro da gasolina no intervalo de três dias consecutivos. No segundo dia, houve um aumento do preço do litro da gasolina de 20% em relação ao primeiro dia e, no terceiro dia, o aumento foi de 10% em relação ao segundo dia. É correto afirmar que o aumento percentual do preço do litro da gasolina do primeiro dia para o terceiro dia foi de

A) 32%.

B) 30%.

C) 12%.

D) 2%.

(Enem) Em 2006, a produção mundial de etanol foi de 40 bilhões de litros e a de biodiesel, de 6,5 bilhões. Neste mesmo ano, a produção brasileira de etanol correspondeu a 43% da produção mundial, ao passo que a produção dos Estados Unidos da América, usando milho, foi de 45%.

Disponível em: planetasustentavel.abril.com.br.Acesso em: 02 maio 2009

Considerando que, em 2009, a produção mundial de etanol seja a mesma de 2006 e que os Estados Unidos produzirão somente a metade de sua produção de 2006, para que o total produzido pelo Brasil e pelos Estados Unidos continue correspondendo a 88% da produção mundial, o Brasil deve aumentar sua produção em, aproximadamente,

A) 22,5%.

B) 50,0%.

C) 52,3%.

D) 65,5%.

E) 77,5%.

(Enem 2024) Uma piscina tem capacidade de 2 500 000 litros. Seu sistema de abastecimento foi regulado para ter uma vazão constante de 6 000 litros de água por minuto. O mesmo sistema foi instalado em uma segunda piscina, com capacidade de 2750000 litros, e regulado para ter uma vazão, também constante, capaz de enchê-la em um tempo 20% maior que o gasto para encher a primeira piscina.

A vazão do sistema de abastecimento da segunda piscina, em litro por minuto, é

A) 8250

B) 7920

C) 6545

D) 5500

E) 5280

(Enem 2023 – PPL) Uma pessoa comprou uma caixa com 25 bombons por 5 reais. Resolveu revendê-los de forma avulsa a um preço único. Não resistindo à tentação, durante a venda, comeu cinco bombons. Obteve, mesmo assim, com a venda dos bombons restantes, um lucro de 20% sobre o valor pago pela caixa.

Qual foi o valor, em real, de venda de cada bombom?

A) 0,20

B) 0,24

C) 0,30

D) 0,35

E) 0,40

(Enem– PPL) No início de janeiro de um determinado ano, uma família decidiu economizar para as férias de julho daquele ano, guardando uma quantia por mês. Eles decidiram que, em janeiro, guardariam R$ 300,00 e, a partir de fevereiro, guardariam, a cada mês, 20% a mais do que no mês anterior. 

Qual foi o total economizado (em real) no primeiro semestre do ano, abandonando, por arredondamento, possíveis casas decimais nesse resultado? 

A) 1 800,00 

B) 2 100,00 

C) 2 160,00 

D) 2 978,00 

E) 3 874,00

(Enem) Um paciente necessita de reidratação endovenosa feita por meio de cinco frascos de soro durante 24 h. Cada frasco tem um volume de 800 mL de soro. Nas primeiras quatro horas, deverá receber 40% do total a ser aplicado. Cada mililitro de soro corresponde a 12 gotas.

O número de gotas por minuto que o paciente deverá receber após as quatro primeiras horas será:

A) 16

B) 20

C) 24

D) 34

E) 40

Em uma escola com 800 alunos, 60% participam de atividades esportivas. Quantos alunos não participam dessas atividades?

A) 320

B) 340

C) 360

D) 400

E) 480

(Enem – PPL) A conta de telefone de uma loja foi, nesse mês, de R$ 200. O valor da assinatura mensal, já incluso na conta, é de R$ 40, o qual dá direito a realizar uma quantidade ilimitada de ligações locais para telefones fixos. As ligações para celulares são tarifadas separadamente. Nessa loja, são feitas somente ligações locais, tanto para telefones fixos quanto para celulares.

Para reduzir os custos, o gerente planeja, para o próximo mês, uma conta de telefone com valor de R$ 80. Para que esse planejamento se cumpra, a redução percentual com gastos em ligações para celulares nessa loja deverá ser de:

A) 25%

B) 40%

C) 50%

D) 60%

E) 75%

(Enem 2024 – PPL) O limite recomendável de carga a ser transportada por um caminhão é 10000 kg. Ao transportar uma carga que excede em 300 kg esse limite, o consumo de combustível é 2% maior que o consumo observado ao transportar 10000 kg. Em uma rodovia, o consumo de combustível desse caminhão é proporcional à quilometragem percorrida, quando considerada uma mesma carga transportada. Sabe-se que, transportando 10000 kg por 90 km nessa rodovia, esse caminhão consome 60 litros de combustível. Suponha que esse caminhão irá transportar uma carga de 10300 kg por 75 km nessa rodovia. Quantos litros de combustível esse caminhão consumirá para efetuar esse transporte?

A) 49,0

B) 50,0

C) 51,0

D) 58,8

E) 61,2