Exercícios sobre Probabilidade condicional
Teste os seus conhecimentos: Faça exercícios sobre Probabilidade condicional e veja a resolução comentada.
Publicado por: Marcos Noé Pedro da SilvaQuestões
-
Questão 1
Ao lançarmos dois dados não viciados, qual a probabilidade de obtermos faces voltadas para cima onde a soma entre elas seja 6?
Nesse caso temos o lançamento de dois dados. O espaço amostral será determinado pelo produto entre os eventos decorrentes de cada universo de resultados possíveis. No dado, o espaço amostral é composto de 6 eventos e como são dois dados temos que o espaço amostral terá 6 x 6 elementos, totalizando 36.
No lançamento dos dois dados as possibilidades de parceria entre as faces para que a soma seja 6, será:
(1 e 5), (5 e 1), (2 e 4), (4 e 2), (3 e 3).
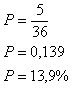
No lançamento de dois dados a probabilidade de obtermos soma das faces voltadas para cima igual a 6 será de aproximadamente 13,9%.
-
Questão 2
No lançamento de uma moeda e um dado, determine a probabilidade de obtermos o resultado dado por (coroa, 1).
Temos que o espaço amostral do dado corresponde a 6 eventos e que o espaço amostral da moeda equivale a 2 eventos. Envolvendo o dado e a moeda temos um espaço amostral de 12 eventos. A probabilidade de obtermos o resultado (coroa, 1) é de 1 em 12. Portanto:
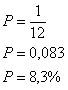
Ao lançarmos um dado e uma moeda, a probabilidade de obtermos o par (coroa, 1) será de aproximadamente 8,3%.
-
Questão 3
Em uma empresa, o risco de alguém se acidentar é dado pela razão 1 em 30. Determine a probabilidade de ocorrer nessa empresa as seguintes situações relacionadas a 3 funcionários:
Todos se acidentarem.
Nenhum se acidentar.
Probabilidade de todos se acidentarem
Como o risco é de 1 em 30 temos que:
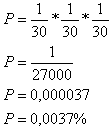
Probabilidade de nenhum se acidentar
Para os acidentados temos a probabilidade de 1 em 30. Nesse caso para os não acidentados temos a probabilidade de 29 em 30. Então:
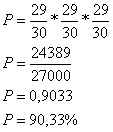
-
Questão 4
(UFF–RJ)
Em um jogo de bingo são sorteadas, sem reposição, bolas numeradas de 1 a 75, e um participante concorre com a cartela reproduzida abaixo. Qual é a probabilidade de que os três primeiros números sorteados estejam nessa cartela?
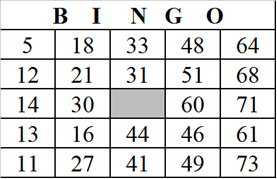
Podemos resolver o exercício utilizando o princípio fundamental da contagem. Observe que a cartela contém 24 números entre um universo de 75 que serão sorteados. A chance dos três primeiros números dessa cartela serem sorteados nas três primeiras rodadas respeita a seguinte ordem:
1º sorteio – 24/75
2º sorteio ¬– 23/74
3º sorteio – 22/73Calculamos a chance realizando o produto entre os eventos:
.gif)
A chance dos três primeiros números sorteados serem da cartela é de 3%.
-
Questão 5
(UFSCar)
Dois dados usuais e não viciados são lançados. Sabe-se que os números observados são ímpares. Então, a probabilidade de que a soma deles seja 8 é:
a) 2/36
b) 1/6
c) 2/9
d) 1/4
e) 2/18No lançamento de dois dados temos que a soma entre as faces ímpares em que o resultado seja 8 é dado pelos pares (5, 3) e (3, 5). Somente 2 eventos satisfazem a situação proposta. Já o espaço amostral estará reduzido ao número de combinações entre resultados ímpares, que é 9. Portanto:
p = 2
9Temos que o item C fornece a resposta correta.