Exercícios sobre Problemas Envolvendo Funções do 2º Grau
(FAAP – SP)
Uma indústria produz, por dia, x unidades de determinado produto, e pode vender tudo o que produzir a um preço de R$ 100,00 a unidade. Se x unidades são produzidas a cada dia, o custo total, em reais, da produção diária é igual a x² + 20x + 700. Portanto, para que a indústria tenha lucro diário de R$ 900,00, qual deve ser o número de unidades produzidas e vendidas por dia?
Função Receita
y = 100 * x
Função Custo
y = x² + 20x + 700
Função Lucro = Receita – Custo
y = 100x – (x² + 20x + 700)
y = 100x – x² – 20x – 700
y = –x² + 80x – 700
Lucro diário de R$ 900,00
–x² + 80x – 700 = 900
–x² + 80x –700 – 900 = 0
–x² + 80x – 1600 = 0
Vamos utilizar Xv na determinação da quantidade de produtos a serem produzidos e vendidos visando o lucro diário de R$ 900,00.
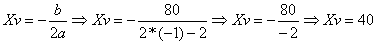
A empresa deverá produzir e vender a quantidade de 40 produtos.
(Cesesp – PE)
Um fabricante vende mensalmente c unidades de um determinado artigo por V(x) = x² – x, sendo o custo da produção dado por C(x) = 2x² – 7x + 8. Quantas unidades devem ser vendidas mensalmente, de modo que se obtenha o lucro máximo?
L(x) = V(x) – C(x)
L(x) = x² – x – (2x² – 7x + 8)
L(x) = x² – x – 2x² + 7x – 8
L(x) = –x² + 6x – 8
Aplicando Xv
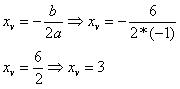
A empresa deverá vender mensalmente 3 unidades do produto.
(PUC – SP)
Uma bola é largada do alto de um edifício e cai em direção ao solo. Sua altura h em relação ao solo, t segundos após o lançamento, é dada pela expressão h = –25t² + 625. Após quantos segundos do lançamento a bola atingirá o solo?
Quando a bola atingir o solo, sua posição será igual a zero, então:
h = 0
0 = –25t² + 625
25t² = 625
t² = 625 / 25
t² = 25
√t² = √25
t = 5
A bola levará 5 segundos para atingir o solo.
(PUC – Campinas – SP)
A trajetória de um projétil foi representada no plano cartesiano por
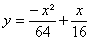
com uma unidade representando um quilômetro. Determine a altura máxima que o projétil atingiu.
Vamos calcular a altura máxima através da fórmula do yv.
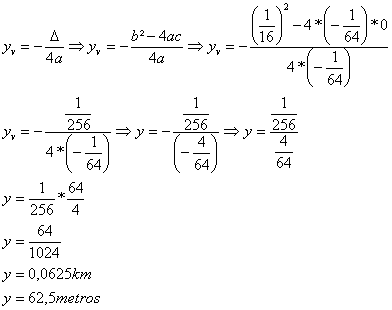
A altura máxima atingida pelo projétil foi de 62,5 metros.
