Exercícios sobre quadriláteros
Uma região possui formato retangular, com perímetro de 36 metros. Se um lado possui o dobro da medida do outro lado, então a área dessa região mede:
A) 64 m²
B) 72 m²
C) 114 m²
D) 144 m²
E) 160 m²
Alternativa B
Se a soma dos seus 4 lados é igual a 36, sendo x a medida do lado menor e 2x a medida do lado maior, temos que:
\(2x+2x+x+x=36\)
\(6x=36\)
\(x=\frac{36}{6}\)
\(x=6\)
Sabendo que x = 6, então 2x = 12. A área do retângulo é o produto da sua base pela sua altura, logo:
\(A=12⋅6\)
\(A=72 m^2\)
Um losango possui diagonal maior medindo 12 cm e diagonal menor medindo 8 cm, então a área desse losango é de:
A) 12 cm²
B) 20 cm²
C) 48 cm²
D) 59 cm²
E) 96 cm²
Alternativa C
\(A=\frac{D\cdot d}{2}\)
Então temos que:
\(A=\frac{12\cdot8}{2}\)
\(A=\frac{96}{2}\)
\(A=48 cm^2\)
Analisando as figuras geométricas a seguir, marque a alternativa que possui aquele que não é considerado um quadrilátero.
A) Cubo
B) Quadrado
C) Retângulo
D) Paralelogramo
E) Trapézio
Alternativa A
Analisando as alternativas, o cubo não é considerado um quadrilátero, pois ele é um sólido geométrico, com 3 dimensões, e não um polígono.
O quintal da Dona Ana possui formato de um trapézio com base menor medindo 4 m e base maior medindo 6 m e 3 m de altura. Dona Ana decidiu gramar toda essa área, com uma grama que custa R$ 6,50 o m². Então o mínimo gasto por Dona Ana para cobrir todo o seu quintal é
A) R$ 65,00
B) R$ 102,00
C) R$ 195,00
D) R$ 216,00
E) R$ 234,00
Alternativa E
Calculando a área do trapézio temos que:
\(A=\frac{(6\cdot4)\cdot3}{2}\)
\(A=\frac{24\cdot3}{2}\)
\(A=\frac{72}{2}\)
\(A=36 m^2\)
Calculando o custo, temos que:
\(36 ⋅6,5 = 234,00 \)
Sobre os quadriláteros, julgue as afirmativas a seguir:
I – Todo quadrado é também um retângulo.
II – Todo retângulo é também um quadrado.
III – Nem todo losango é um quadrado.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa B
I – Todo quadrado é também um retângulo. (verdadeira)
II – Todo retângulo é também um quadrado. (falsa)
Ainda que todo quadrado seja um retângulo, a recíproca não é verdadeira, ou seja, nem todo retângulo é um quadrado.
III – Nem todo losango é um quadrado. (verdadeira)
Uma região no formato de um quadrado possui perímetro medindo 26 metros. Então a área dessa região mede:
A) 24,38 m²
B) 29,16 m²
C) 38,44 m²
D) 42,25 m²
E) 54,20 m²
Alternativa D
Sabemos que o perímetro é a soma dos 4 lados do quadrado e que esses lados são todos congruentes, logo temos que:
\(P=4l\)
\(4l = 26\)
\(l=\frac{26}{4}\)
\(l=6,5\)
Se o valor da medida do lado é 6,5 m, então o valor da área é de:
\(A=l^2\)
\(A=6,5^2\)
\(A=42,25 m^2\)
Analise a figura geométrica a seguir:
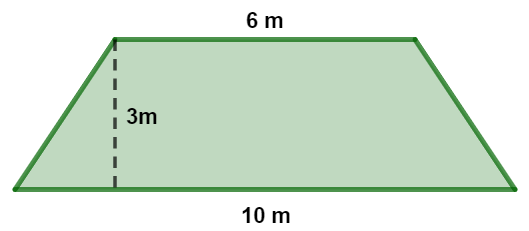
A área dessa figura mede:
A) 30 m²
B) 40 m²
C) 60 m²
D) 90 m²
E) 120 m²
Alternativa D
Calculando a área desse trapézio, temos que:
\(A=\frac{(10+6)\cdot3}{2}\)
\(A=\frac{60\cdot3}{2}\)
\(A=\frac{180}{2}\)
\(A=90 m^2\)
O retângulo a seguir possui 26 cm de perímetro.
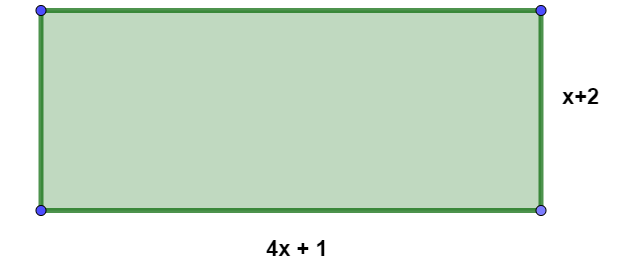
Então o valor de x em centímetros é:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa B
Calculando o valor de x:
\(4x+1+4x+1+x+2+x+2=26\)
\(10x+6=26\)
\(10x=26-6\)
\(10x=20\)
\(x=\frac{20}{10}\)
\(x=2\)
(Enem 2017) Um fabricante recomenda que, para cada m² do ambiente a ser climatizado, são necessários 800 BTUh, desde que haja até duas pessoas no ambiente. A esse número devem ser acrescentados 600 BTUh para cada pessoa a mais, e também para cada aparelho eletrônico emissor de calor no ambiente. A seguir, encontram-se as cinco opções de aparelhos desse fabricante e suas respectivas capacidades térmicas:
- Tipo I: 10 500 BTUh
- Tipo II: 11 000 BTUh
- Tipo III: 11 500 BTUh
- Tipo IV: 12 000 BTUh
- Tipo V: 12 500 BTUh
O supervisor de um laboratório precisa comprar um aparelho para climatizar o ambiente. Nele ficarão duas pessoas mais uma centrífuga que emite calor. O laboratório tem forma de trapézio retângulo, com as medidas apresentadas na figura.
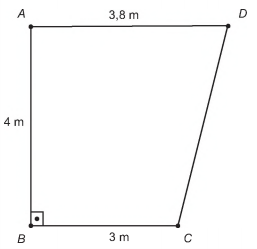
Para economizar energia, o supervisor deverá escolher o aparelho de menor capacidade térmica que atenda às necessidades do laboratório e às recomendações do fabricante.
A escolha do supervisor recairá sobre o aparelho do tipo
A) I.
B) II.
C) III.
D) IV.
E) V.
Alternativa C
Sabemos que o ambiente possui formato de um trapézio, então calculando a sua área temos que:
\(A=\frac{B+b)h}{2}\)
\(A=\frac{(3,8+3)\cdot4}{2}\)
\(A=\frac{6,8⋅4}{2}\)
\(A=13,6 m^2\)
Se a cada m² são gastos 800 BTUh, então temos que 13,6 ⋅ 800 = 10.880. Por fim somaremos 600 BTUh referentes ao objeto transmissor de calor:
\(10.880+600=11.480\)
O que melhor atende às condições é o aparelho III.
Um losango possui perímetro igual a 16 cm. Então a medida do lado desse losango é de:
A) 10 cm
B) 8 cm
C) 6 cm
D) 4 cm
E) 2 cm
Alternativa D
Sabemos que o losango possui todos os lados congruentes. Sendo assim, temos que:
\(4l = 16\)
\(l=\frac{16}{4}\)
\(l= 4 cm\)
Então a medida do lado do losango é de 4 cm.
Um retângulo possui perímetro igual a 30 cm. Se um lado mede 2/3 do outro lado, então a medida do maior lado desse retângulo é de:
A) 10 cm
B) 9 cm
C) 8 cm
D) 7 cm
E) 6 cm
Alternativa 9
Sendo x o maior lado, temos que:
\(2(x+\frac {2}{3}x)=30\)
\(x+\frac{2}{3}x=\frac{30}{2}\)
\(x+\frac{2}{3}x=15\)
\(\frac{3x+2x}{3}=\frac{45}{3}\)
\(3x+2x=45\)
\(5x=45\)
\(x=\frac{45}{5}\)
\(x= 9 cm \)
(Enem 2015) O Esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.
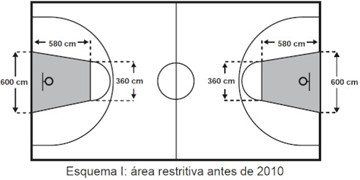
Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
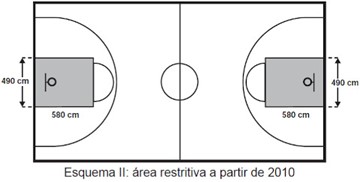
Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
A) aumento de 5800 cm².
B) aumento de 75400 cm².
C) aumento de 214600 cm².
D) diminuição de 63800 cm².
E) diminuição de 272600 cm².
Alternativa A
Calculando a área do garrafão no esquema I, temos que:
\(A=\frac{(B+b)\cdot h}{2}\)
\(A=\frac{(600+380)\cdot580}{2}\)
\(A=\frac{980\cdot580}{2}\)
\(A=\frac{556800}{2}\)
\(A=278400\)
Agora, calculando a área do esquema II, temos que:
\(A=b ⋅h\)
\(A=580 ⋅490\)
\(A=284200\)
Calculando a diferença:
\(284200-278400=5800 cm^2\)
