Exercícios sobre radiciação
Simplifique a expressão \(\sqrt{48}\).
A) \( 8\sqrt6\)
B) \( 4\sqrt3\)
C) \( 7\sqrt2\)
D) \( 8\sqrt3\)
E) \( 24\sqrt2\)
Alternativa B.
Primeiramente vamos decompor 48 em fatores primos:
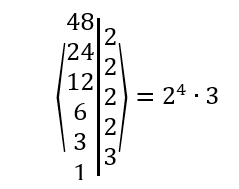
\({48=2}^4\cdot3\)
Agora, simplificando o radical, temos: \(\sqrt{48}=\sqrt{2^4\cdot3}=2^2\sqrt3=4\sqrt3\).
Simplifique a expressão \(\sqrt{200}\).
A) \( 2\sqrt{10}\)
B) \( 40\sqrt5\)
C) \( 20\sqrt5\)
D) \( 10\sqrt2\)
E) \( 5\sqrt{40}\)
Alternativa D.
Observamos que \(\sqrt{200}=\sqrt{2\cdot100}\). Como \(\sqrt{100}=10\), temos que:
\(\sqrt{200}=10\cdot\sqrt2\)
Calcule \(\sqrt{15}\sqrt6\).
A) \( 6\sqrt3\)
B) \( 4\sqrt3\)
C) \( 10\sqrt3\)
D) \( 3\sqrt5\)
E) \( 3\sqrt{10}\)
Alternativa E.
Multiplicamos os radicais: \(\sqrt{15\cdot6}=\sqrt{90}\). Agora fatoramos 90 contendo algum quadrado prefeito.
\(90=9\cdot10, \ logo \ \sqrt{90}=\sqrt{9\cdot10}=3\sqrt{10}.\)
Calcule \(\frac{\sqrt{72}}{\sqrt3}\).
A) \( 2\sqrt{12}\)
B) \( 2\sqrt6\)
C) \( 4\sqrt6\)
D) \( 6\sqrt4\)
E) \( 3\sqrt7\)
Alternativa B.
Primeiro observamos que os índices dos radicais são iguais, logo podemos escrever:
\(\frac{\sqrt{72}}{\sqrt3}=\sqrt{\frac{72}{3}}=\sqrt{24}\)
Escrevendo esse número contendo um quadrado perfeito, temos:
\(\sqrt{24}=\sqrt{4\cdot6}=2\sqrt6\)
Simplifique a expressão \(\sqrt[3]{3+\sqrt{15+\sqrt{36+4\sqrt{256}}}}\).
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa A.
Precisamos resolver as raízes mais internas \(\sqrt[3]{3+\sqrt{15+\sqrt{36+4\sqrt{\mathbf{256}}}}}\).
Primeiro vamos resolver \(\sqrt{256}\) e, para isso, vamos fatorar o número:
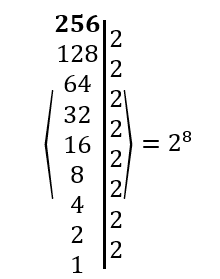
\(\sqrt{256}=\sqrt{2^8}=2^4=16\)
Vamos substituir esse resultado na expressão acima:
\(\sqrt[8]{3+\sqrt{15+\sqrt{36+4\cdot16}}}\)
\(\sqrt[3]{3+\sqrt{15+\sqrt{36+64}}}\)
\(\sqrt[3]{3+\sqrt{15+\sqrt{100}}}\)
\(\sqrt[3]{3+\sqrt{15+10}}\)
\(\sqrt[3]{3+\sqrt{25}}\)
\(\sqrt[3]{3+5}\)
\(\sqrt[3]{8}\)
\(\sqrt[3]{2^3}\)
\(2\)
Marque a alternativa que representa a soma das raízes \(\sqrt{48}+\sqrt{75}\).
A) \( 5\sqrt7\)
B) \( 9\sqrt3\)
C) \( 3\sqrt7\)
D) \( 11\sqrt3\)
E) \( 61,5\)
Alternativa B.
Devemos fatorar os valores que estão dentro das raízes acima e organizar sua soma.
\(\sqrt{48}=\sqrt{16\cdot3}=4\sqrt3\)
\(\sqrt{75}=\sqrt{25\cdot3}=5\sqrt3\)
Logo, \(\sqrt{48}+\sqrt{75}=\mathbf{4}\sqrt3+\mathbf{5}\sqrt3=\mathbf{9}\sqrt3\).
Resolva a expressão e marque a alternativa correta:
\(\sqrt{0,16}\sqrt[3]{0,008}\)
A) 0,8
B) 0,08
C) 0,04
D) 0,4
E) 0,2
Alternativa B.
Devemos escrever as raízes de forma a obter uma fração com números inteiros.
\(\sqrt{0,16}=\sqrt{\frac{16}{100}}=\frac{4}{10}=0,4\)
\(\sqrt[3]{0,008}=\sqrt[3]{\frac{8}{1000}}=\frac{\sqrt[3]{2^3}}{\sqrt[3]{{10}^3}}=\frac{2}{10}=0,2\)
Logo, \(\sqrt{0,16}\sqrt[3]{0,008}=0,4⸳0,2=0,08\).
Sabendo que \(x=\sqrt{3-\sqrt5}\sqrt{3+\sqrt5}\), determine o valor de \(x-1\).
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa A.
Vamos primeiro calcular o produto dos valores internos dessas raízes:
\(\left(3-\sqrt5\right)\left(3+\sqrt5\right)=9+3\sqrt5-3\sqrt5+\sqrt{25}=9-5=4\)
\(\sqrt{3-\sqrt5}\sqrt{3+\sqrt5}=\sqrt4=2\)
Logo, \(x=2 \ e\ x-1=\mathbf{2}-\mathbf{1}=\mathbf{1}\).
Calcule o valor da expressão \({(\sqrt{6^{\sqrt{100}}})}^{0,4}\).
A) 6
B) 36
C) \( \sqrt6\)
D) 216
E) 0,6
Alternativa B.
Observemos a resolução feita dos fatores internos para os externos:
\({(\sqrt{6^{\sqrt{100}}})}^{0,4}{=(\sqrt{6^{10}})}^{0,4}={(6^\frac{10}{2})}^{0,4}={{(6}^5)}^{0,4}=6^{5\bullet0,4}=6^2=36\)
Calcule o valor da expressão \({({(0,25)}^{0,5})}^{\sqrt{0,16}}\).
A) \( \sqrt[5]{0,25}\)
B) \( \sqrt[5]{4}\)
C) \( \sqrt[5]{25}\)
D) \( \sqrt[5]{16}\)
E) \( \sqrt[5]{2}\)
Alternativa B.
Primeiro vamos reescrever a equação transformando os números acima em frações.
\({({(0,25)}^{0,5})}^{\sqrt{0,16}}={({(\frac{1}{4})}^\frac{1}{2})}^{\sqrt{\frac{16}{100}}}={(\sqrt{\frac{1}{4}})}^\frac{4}{10}={(\frac{1}{2})}^\frac{2}{5}=\sqrt[5]{2^2}=\sqrt[5]{4}\)
Calcule o valor da expressão \({({729)}^{0,333\ldots})}^{0,5}\).
A) 7
B) 6
C) 5
D) 4
E) 3
Alternativa E.
Primeiro devemos transformar a dízima em fração: \(0,333\ldots=\frac{3}{9}=\frac{1}{3}\)
\({({729)}^{0,333\ldots})}^{0,5}={({729)}^\frac{1}{3})}^{0,5}={(\sqrt[3]{729})}^{0,5}={(\sqrt[3]{9^3})}^{0,5}=9^{0,5}=9^\frac{1}{2}=\sqrt9=3\)
Calcule o valor da expressão \({({1000.000.000)}^{0,4444\ldots})}^{0,25}\).
A) 1
B) 10
C) 100
D) 1000
E) 100000
Alternativa C.
Primeiro devemos transformar a dízima em fração: \(0,444\ldots=\frac{4}{9}\)
Logo,
\(\left({1000.000.000)}^{0,444\ldots}\right)^{0,3}=\left({1000.000.000)}^\frac{4}{9}\right)^{0,5}\)
\(={(\sqrt[9]{{{(10}^9)}^4})}^{0,5}={10}^{4\cdot0,5}={10}^2=100\)
