Exercícios sobre Raiz de uma Equação do 2º Grau
(UCS-RS)
Se uma das raízes da equação 2x² – 3px + 40 = 0 é 8, determine o valor de p.
2x² – 3px + 40 = 0
Se 8 é uma das raízes da equação, então temos que x = 8.
2 * 8² – 3 * p * 8 + 40 = 0
2 * 64 – 24 * p + 40 = 0
128 – 24p + 40 = 0
–24p = –128 –40
–24p = –168 * (–1)
24p = 168
p = 7
O valor de p para que a equação 2x² – 3px + 40 = 0 tenha uma das raízes igual a 8 é 7.
S = {p Є R / p = 7}
Determine o valor de m na equação x² – (m + 5)x + 36 = 0, de modo que as raízes sejam reais e diferentes.
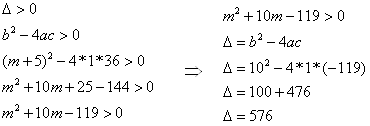
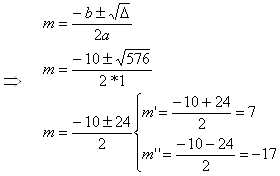
O valor de m para que a equação x² – (m + 5)x + 36 = 0 tenha raízes reais e diferentes é m = 7 ou m = –17.
S = {p Є R / m = 7 ou m = –17}
Dada a equação 9x² + 12x + 2m = 0, determine os possíveis valores de m para que a equação não possua raízes reais.
∆ < 0
b² – 4ac < 0
12² – 4 * 9 * 2m < 0
144 – 72m < 0
144 < 72m
m > 2
Para que a equação 9x² + 12x + 2m = 0, não possua raízes reais o valor de m será maior que 2.
S = {p Є R / m > 2}
A equação do 2º grau x² – kx + 9 = 0, assume as seguintes condições de existência dependendo do valor da variável k:
Duas raízes reais e distintas: ∆ > 0.
Duas raízes reais e iguais: ∆ = 0.
Nenhuma raiz real: ∆ < 0.
Para que a equação tenha raízes reais e iguais, qual deve ser o valor da variável k?
∆ = 0
b² ¬– 4ac = 0
(¬–k)² – 4 * 1 * 9 = 0
k² – 36 = 0
k² = 36
k = 6 ou k = –6
O valor de k na equação x² – kx + 9 = 0 deve assumir os seguintes valores:
k = 6 ou k = –6.
S = {k Є R / k = 6 e k = –6}
Determine o valor de p na equação px² – 3x – 2 = 0, com p ≠ 0 de modo que a soma das raízes seja igual a 12.
.gif)
S = {p Є R / p = 3/20}
Calcule o valor de k na equação x² – 10x – m + 8 = 0, com m ≠ 0, de modo que o produto das raízes seja igual a – 2.
.gif)
S = {m Є R / m = 10}
Determine o valor de p na equação 6x² – 11x + (p – 1) = 0, para que o produto das raízes seja igual a 2/3.
.gif)
S = {p Є R / p = 5}
Calcule o valor de k na equação x² – kx + 36 = 0, de modo que uma das raízes seja o quádruplo da outra.
.gif)
S = {k Є R / k = 3 ou k = –3}
