Exercícios sobre Raiz de uma Função do 1º Grau
Teste os seus conhecimentos: Faça exercícios sobre Raiz de uma Função do 1º Grau e veja a resolução comentada.
Publicado por: Marcos Noé Pedro da SilvaQuestões
-
Questão 1
Dada a função f: R → R definida por f(x) = x² – 2, calcule:
a) f(–1)
b) f(1)
c) f(0)
f(x) = x² – 2
a)
f(–1) = (–1)² – 2
f(–1) = 1 – 2
f(–1) = –1b)
f(1) = 1² – 2
f(1) = 1 – 2
f(1) = – 1c)
f(0) = 0² – 2
f(0) = – 2
-
Questão 2
Determine os números reais a e b na função f: R → R definida por f(x) = ax + b, sabendo que f(2) = 0 e f(0) = –4.
f(x) = ax + b
f(2) = 2a + b
2a + b = 0f(0) = 0 * a + b
b = –4Sistema de equações:
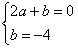
2a + b = 0
2a – 4 = 0
2a = 4
a = 2
Os valores de a e b são 2 e –4 respectivamente, formando a função f(x) = 2x – 4. -
Questão 3
Dada a função f(x) = x² – 4x + 6, determine os valores de x para que se tenha imagem igual a 3.
f(x) = x² – 4x + 6
f(x) = 3
x² – 4x + 6 = 3
x² – 4x + 6 – 3 = 0
x² – 4x + 3 = 0∆ = b² – 4ac
∆ = (–4)² – 4 * 1 * 3
∆ = 16 – 12
∆ = 4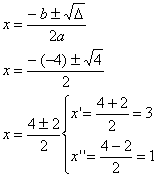
Os valores de x são: x = 1 ou x = 3.
-
Questão 4
(UFMT)
Considerando a função f(x) = 3x² – 4x + 7, diga se a expressão f(1) + f(–1) = 2 * f(0) é válida para a função.
f(x) = 3x² – 4x + 7
f(1) + f(–1) = 2 * f(0)
f(1) = 3 * 1² – 4 * 1 + 7
f(1) = 3 – 4 + 7
f(1) = 6f(–1) = 3 * (–1)² – 4 * (–1) + 7
f(–1) = 3 + 4 + 7
f(–1) = 142 * f(0) = 2 * [3 * (0)² – 4 * 0 + 7]
2 * f(0) = 2 * [ 7 ]
2 * f(0) = 14f(1) + f(–1) = 2 * f(0)
6 + 14 = 14
20 = 14 (impossível)
A expressão f(1) + f(–1) = 2 * f(0) não é válida para a função f(x) = 3x² – 4x + 7.
-
Questão 5
Dada as funções f(x) = 2x – 3 e g(x) = 4 – x, determine:
a) f(–1)
b) f(x + 1)
c) g(4)
d) g(x – 2)
a)
f(x) = 2x – 3
f(–1) = 2 * (–1) – 3
f(–1) = –2 –3
f(–1) = –5b)
f(x + 1) = 2x – 3
f(x + 1) = 2 * (x + 1) – 3
f(x + 1) = 2x + 2 – 3
f(x + 1) = 2x – 1c)
g(x) = 4 – x
g(4) = 4 – 4
g(4) = 0d)
g(x) = 4 – x
g(x – 2) = 4 – (x – 2)
g(x – 2) = 4 – x + 2
g(x – 2) = 6 – x
-
Questão 6
Sabendo que f(x – 1) = 2x + 3, calcule:
a) f(1)
b) f(3)
A)
f(x – 1) = 2x + 3, para f(1)
x – 1 = 1
x = 1 + 1
x = 2f(2 – 1) = 2 * 2 + 3
f(1) = 4 + 3
f(1) = 7B)
f(x – 1) = 2x + 3, para f(3)
x – 1 = 3
x = 3 + 1
x = 4f(4 – 1) = 2 * 4 + 3
f(3) = 8 + 3
f(3) = 11
-
Questão 7
(U. Católica de Salvador-BA)
Seja a função f de R em R definida por f(x) = 54x + 45. Determine o valor de f(2541) – f(2540).
a) 1
b) 54
c) 90
d) 99
e) 108
f(x) = 54x + 45
f(2541) – f(2540) = (54 * 2541 + 45) – (54 * 2540 + 45)
f(2541) – f(2540) = 137 214 + 45 – (137 160 + 45)
f(2541) – f(2540) = 137259 – 137205
f(2541) – f(2540) = 54Resposta: item b.
-
Questão 8
(U. F. Viçosa-MG)
Uma função f é dada por f(x) = ax + b, em que a e b são números reais. Considerando que f(–1) = 3 e f(1) = –1, determine f(3).
a) 1
b) 3
c) –3
d) 5
e) –5
f(–1) = 3
f(–1) = (–1) * a + b
–a + b = 3f(1) = –1
f(1) = 1 * a + b
a + b = – 1Sistema de equações
.gif)
Isolando b na 1ª equação:
–a + b = 3
b = 3 + aSubstituindo b na 2ª equação:
a + b = – 1
a + 3 + a = – 1
2a = – 1 – 3
2a = – 4
a = –4/2
a = –2Calculando b
b = 3 + a
b = 3 – 2
b = 1Determinando a função de acordo com f(x) = ax + b → f(x) = –2x + 1.
Calculando f(3)
f(x) = –2x + 1
f(3) = –2 * (3) + 1
f(3) = – 6 + 1
f(3) = – 5O valor de f(3) na equação é igual a –5.
Resposta: item e.