Leia conteúdos de todas as disciplinas
Exercícios sobre retas
A reta é considerada uma figura unidimensional porque:
A) possui comprimento e largura.
B) possui apenas comprimento.
C) é formada por curvas.
D) possui comprimento, largura e profundidade.
E) pode ser representada apenas no espaço tridimensional
Alternativa B.
A reta possui uma única dimensão, ou seja, somente comprimento.
Qual das opções a seguir apresenta corretamente a diferença entre reta, semirreta e segmento de reta?
A) A reta tem início e fim; a semirreta tem fim; o segmento é infinito.
B) A reta é limitada; a semirreta é curva; o segmento é pontilhado.
C) A reta não tem início nem fim; a semirreta tem início e não tem fim; o segmento tem início e fim.
D) A reta é bidimensional; a semirreta é unidimensional; o segmento é tridimensional.
E) Todos possuem início e fim definidos.
Alternativa C.
A reta é infinita, logo, sabemos que: a reta não tem início nem fim.
A semirreta tem ponto inicial definido, porém não é limitada do outro lado, logo, sabemos que: a semirreta tem início e não tem fim.
Por fim, o segmento de reta é delimitado, logo, sabemos que: o segmento tem início e fim.
Duas retas são ditas paralelas quando:
A) se cruzam em um único ponto.
B) pertencem ao mesmo plano e nunca se cruzam.
C) formam um ângulo de 90°.
D) estão contidas em planos diferentes.
E) coincidem perfeitamente uma com a outra.
Alternativa B.
Duas retas pertencentes ao mesmo plano são paralelas quando elas não possuem nenhum ponto em comum.
Duas retas são conhecidas como coincidentes quando:
A) elas se cruzam em um único ponto.
B) possuem pontos em comum, mas não são uma mesma reta.
C) não têm nenhum ponto em comum.
D) são duas retas com todos os pontos em comum.
E) estão em planos diferentes.
Alternativa D.
Dizer que duas retas são coincidentes significa dizer que essas retas possuem infinitos pontos em comum, ou seja, todos os pontos que pertencem a uma reta também pertencem à outra reta. Sendo assim, essas duas retas, na verdade, são uma mesma reta.
Duas retas concorrentes podem ser chamadas de perpendiculares quando:
A) elas não se cruzam.
B) elas coincidem totalmente.
C) elas se cruzam em qualquer ângulo diferente de 90°.
D) elas se cruzam formando um ângulo de 180°.
E) elas se cruzam formando ângulos retos.
Alternativa E.
Duas retas são conhecidas como retas perpendiculares quando elas se cruzam formando um ângulo reto, ou seja, um ângulo que possui exatamente 90º.
Duas retas são chamadas de concorrentes quando:
A) coincidem perfeitamente em todos os seus pontos.
B) estão no mesmo plano e nunca se encontram, mantendo sempre a mesma distância.
C) estão em planos diferentes e, por isso, não se cruzam.
D) se cruzam em mais de um ponto.
E) estão no mesmo plano e se cruzam em exatamente um ponto.
Alternativa E.
Duas retas são conhecidas como retas concorrentes quando elas se cruzam possuindo um único ponto em comum.
Sobre as possíveis posições relativas entre retas, faça as correspondências:
I. Retas concorrentes
II. Retas coincidentes
III. Retas paralelas
( ) Retas que não possuem nenhum ponto em comum.
( ) Retas que possuem um único ponto em comum.
( ) Retas que possuem todos os pontos em comum.
A ordem correta é:
A) I, II e III.
B) II, I e III.
C) III, I e II.
D) III II e I.
E) I, III e II.
Alternativa C.
Retas que não possuem nenhum ponto em comum são retas paralelas. III
Retas que se cruzam em um único ponto são retas concorrentes. I
Retas que possuem todos os pontos em comum são retas coincidentes. II
A ordem correta é III, I e II.
Analise a imagem a seguir:
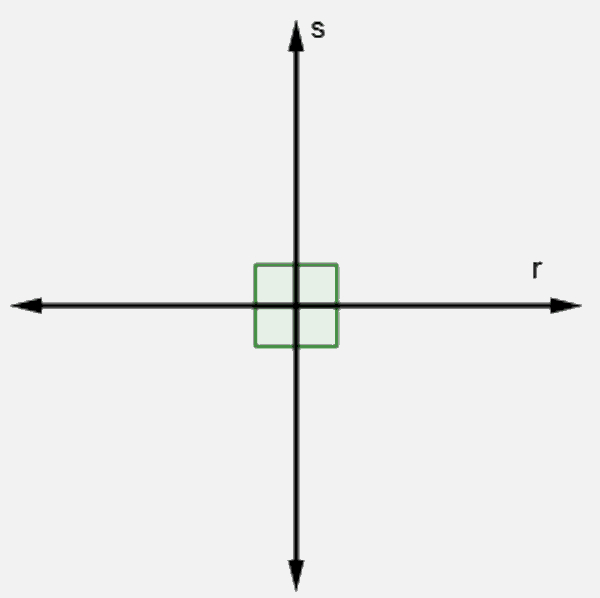
Sabendo que r e s são duas retas, podemos afirmar que:
A) r ∥ s
B) r ≡ s
C) r ⋕ s
D) r ⊥ s
E) r < s
Alternativa D.
Analisando a relação entre a reta r e a reta s, podemos perceber que essas retas são concorrentes e que, além disso, formam um ângulo reto, logo, essas retas são perpendiculares, ou seja r ⊥ s.
Quando duas retas paralelas são cortadas por uma transversal, formam-se oito ângulos.
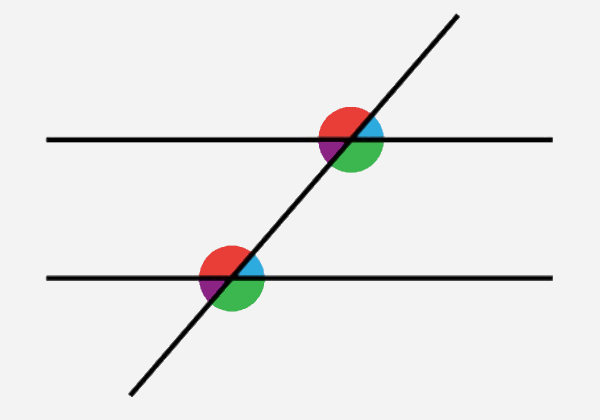
Sobre as propriedades desses ângulos, analise as afirmativas a seguir:
I. Ângulos alternos internos são congruentes.
II. Ângulos correspondentes são sempre suplementares.
III. Dois ângulos colaterais internos são suplementares.
Assinale a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
E) Nenhuma das afirmativas é verdadeira.
Alternativa B.
I. Ângulos alternos internos são congruentes. (Verdadeiro)
Quando duas retas paralelas são cortadas por uma transversal, os ângulos alternos internos têm a mesma medida.
II. Ângulos correspondentes são sempre suplementares. (Falso)
Ângulos correspondentes são congruentes, ou seja, têm a mesma medida, logo, não são suplementares (que somam 180°).
III. Dois ângulos colaterais internos são suplementares. (Verdadeiro)
Os ângulos colaterais internos (também chamados de conjugados internos) somam 180° quando as retas são paralelas.
Em uma cidade, as ruas principais são construídas de forma que nunca se cruzam, mantendo-se sempre a mesma distância entre elas para facilitar o trânsito.
Essas ruas que nunca se encontram e estão no mesmo plano são chamadas de:
A) retas concorrentes, pois se cruzam em vários pontos.
B) retas coincidentes, pois estão exatamente uma sobre a outra.
C) retas paralelas, pois estão no mesmo plano e nunca se cruzam.
D) retas transversais, pois cortam outras ruas.
E) segmentos de reta, pois têm um início e um fim.
Alternativa C.
Retas paralelas são retas que nunca se cruzam, preservando sempre a mesma distância entre elas, logo, essas duas ruas são paralelas entre si.
Em uma cidade planejada, duas avenidas paralelas cortam toda a extensão da região. Para facilitar o trânsito e a construção de passarelas, uma terceira rua foi construída, cruzando essas duas avenidas em diferentes pontos.
Essa terceira rua, que intercepta as duas avenidas paralelas, é chamada de:
A) reta coincidente, pois fica exatamente sobre uma das avenidas.
B) reta paralela, pois não cruza as outras ruas.
C) reta transversal, pois corta duas ou mais retas (avenidas) no mesmo plano.
D) reta oblíqua, pois nunca encontra outras ruas.
E) segmento de reta, pois possui início e fim definidos.
Alternativa C.
Uma reta transversal é definida como uma reta que intercepta duas ou mais retas distintas que estão no mesmo plano. Como há duas retas paralelas, e foi construída uma terceira cortando as duas, então, essa rua é uma reta transversal.
Em um projeto de arquitetura, duas linhas foram desenhadas para representar uma parede no mesmo plano. Com o passar do tempo, percebeu-se que as duas linhas estavam exatamente sobrepostas, representando a mesma parede.
Essas duas linhas, que ocupam o mesmo lugar no plano, são chamadas de:
A) retas paralelas, pois nunca se cruzam.
B) retas concorrentes, pois se cruzam em um ponto.
C) retas transversais, pois cortam outras retas.
D) retas coincidentes, pois ocupam exatamente o mesmo lugar.
E) segmentos de reta, pois têm começo e fim.
Alternativa D.
Retas coincidentes são retas que possuem todos os seus pontos em comum, ou seja, elas estão exatamente sobrepostas no mesmo plano. No exemplo, as duas linhas desenhadas para representar a mesma parede são coincidentes porque ocupam o mesmo lugar.
Ferramentas
