Exercícios sobre seno e cosseno de ângulos suplementares
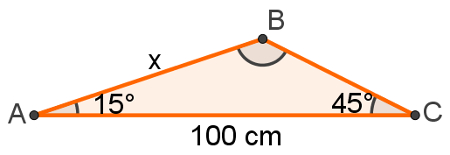
No triângulo a seguir, qual é a medida do segmento AB, representado pela letra x?
a) 10√6/3 cm
b) 10√3/3 cm
c) 5√6/3 cm
d) 10√6 cm
e) 10√2/3 cm
Para resolver esse problema, devemos usar lei dos senos, que envolve o lado AB e o ângulo C, o lado AC e o ângulo B. Como não conhecemos a medida do ângulo B, podemos descobri-la:
A + B + C = 180
15 + B + 45 = 180
60 + B = 180
B = 180 – 60
B = 120°
Portanto, na lei dos cossenos, teremos:
x = 10
sen45° sen120°
Agora, observe que o sen120° = sen(180° – 120°) = sen60°. Então:
x = 10
sen45 ° sen60°
x·sen60° = 10·sen45°
x·√3 = 10·√2
2 2
x = 10√2
√3
x = 10√6
3
Alternativa A
É possível encontrar valores equivalentes para seno e cosseno de ângulos maiores do que 90°, usando as propriedades adequadas para isso. Qual é o cosseno do ângulo de 150°?
a) √3/2
b) – (√3/2)
c) ½
d) – ½
e) – (√2/2)
Para determinar o cosseno de um ângulo maior do que 90°, basta usar a seguinte fórmula:
cosα = – cos(180° – α)
Então:
cos150° = – cos(180° – 150°)
cos150° = – cos30°
cos150° = – (√3/2)
Alternativa B
A soma do seno do ângulo de 150° com o cosseno do ângulo de 120° é igual a:
a) 1
b) 2
c) 0
d) 0,5
e) – 1
Usando a fórmula para determinar o seno do ângulo suplementar, teremos:
senα = sen(180° – α)
sen150° = sen(180° – 150°)
sen150° = sen30°
sen150° = 0,5
Usando a fórmula para determinar o cosseno do ângulo suplementar, teremos:
cosα = – cos(180° – α)
cos120° = – cos(180° – 120°)
cos120° = – cos60°
cos120° = – 0,5
A soma dos dois resultados é:
0,5 – 0,5 = 0
Alternativa C
É possível encontrar valores equivalentes para seno e cosseno de ângulos maiores do que 90°, usando as propriedades relacionadas a eles. Tendo em vista isso, qual é o seno do ângulo de 132°, sabendo que o seno de 48° é igual a 0,73?
a) 0,73
b) 0,5
c) 1,46
d) 0,36
e) 1
Utilizando a fórmula para determinar o seno de ângulos suplementares, teremos:
senα = sen(180° – α)
sen132° = sen(180° – 132°)
sen150° = sen48°
sen150° = 0,73
Alternativa A
