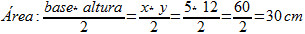Exercícios sobre Sistemas de Equações do 1º e do 2º Grau

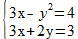
Vamos resolver este sistema utilizando o método da adição. Para tanto, vamos multiplicar a primeira equação por -1.

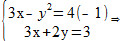
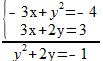
Utilizando Bháskara, podemos resolver a equação encontrada:

y² + 2y = -1 => y² + 2y +1 = 0, onde a = 1, b = 2 e c = 1
∆ = b² - 4 * a * c
∆ = 2² - 4 * 1 * 1
∆ = 4 - 4
∆ = 0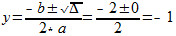

y = - 1

Vamos agora substituir o valor de y na 2ª equação:

3x + 2y = 3
3x + 2 * (- 1) = 3
3x - 2 = 3
3x = 5
x =   5  
        3

Então a solução do sistema é o par ordenado (  5  , - 1) .
                                                                                        3

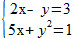
Para resolver este sistema é indicado que utilizemos o método da substituição. Portanto, na primeira equação vamos isolar a variável y:

2x - y = 3 => y = 2x - 3

Vamos agora substituir a expressão encontrada para y na segunda equação:

5x + y² = 1
5x + (2x - 3)² = 1 → Utilizando o quadrado da soma temos: (2x - 3)² = 4x² - 12x + 9
5x + 4x² -12x +9 = 1
4x² - 7x + 8 = 0 → Para utilizarmos Bháskara, façamos a = 4, b = - 7 e c = 8
∆ = b² - 4 * a * c
∆ = 7² - 4 * 4 * 8
∆ = 49 - 128
∆ = - 79

Dentro do conjunto dos Reais, não conseguimos encontrar solução para 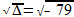. Portanto, não existe par ordenado de números reais que seja solução desse sistema, ou seja, os gráficos das equações não se interceptam em nenhum ponto.

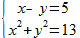
O método mais indicado para aplicarmos na resolução desse sistema é o método da substituição. Para tanto, vamos isolar a variável x na primeira equação:

x - y = 5 => x = 5 + y

Vamos agora substituir x na 2ª equação:

x² + y² = 13
(5 + y)² + y² = 13
25 + 10y + y² + y² = 13
2y² + 10y + 12 = 0 → Para facilitar nossos cálculos, vamos dividir todos os números da equação por 2:

y² + 5y + 6 = 0 → Para utilizarmos Bháskara, façamos a = 1, b = 5 e c = 6

∆ = b² - 4 * a * c
∆ = 5² - 4 * 1 * 6
∆ = 25 - 24
∆ = 1

Temos então:

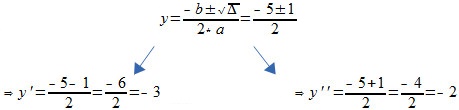
Se y = -3, então:                                                   Se y = -2, então:
x = 5 + y                                                                   x = 5 + y
x = 5 + (-3)                                                                x = 5 + (-2)
x = 2                                                                         x = 3

Portanto, o sistema possui duas soluções reais: (2, -3) e (3, -2).

Antes de resolvermos essa questão é recomendado que você faça uma revisão sobre triângulo retângulo e sobre o cálculo de sua área.

Pelo Teorema de Pitágoras, temos que:

Hipotenusa² = cateto² = cateto²
13² = x² + y² => x² + y² = 169

Pela definição de perímetro, podemos afirmar que:

x + y +13 = 30
x + y = 17

Podemos então montar o sistema de equações:

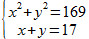
Aplicando o método da substituição, podemos isolar a variável x na segunda equação:

x + y = 17
x = 17 - y

Vamos agora substituir na primeira equação a expressão encontrada para x:

x² + y² = 169
(17 - y)² + y² = 169
289 - 34y + y² + y² = 169
2y² - 34y + 120 = 0 → Para facilitar nossos cálculos, vamos dividir todos os números da equação por 2:

y² - 17y + 60 = 0 → Para utilizarmos Bháskara, façamos a = 1, b = -17 e c = 60
∆ = b² - 4 * a * c
∆ = (-17)² - 4 * 1 * 60
∆ = 289 - 240
∆ = 49

Temos então:

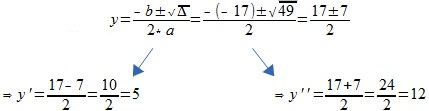
Se y = 5, então:                                                Se y = 12, então:
x = 17 - y                                                              x = 17 - y
x = 17 - 5                                                              x = 17 - 12
x = 12                                                                   x = 5

Pelo enunciado do problema, temos que x