Exercícios sobre termo geral da PA
Com esta lista de exercícios sobre termo geral da PA, você verá se sabe encontrar a posição de um termo a partir de seu valor ou encontrar o próprio termo, dada sua posição.
Publicado por: Luiz Paulo Moreira SilvaQuestões
-
Questão 1
(UFRGS) Em uma progressão aritmética em que o primeiro termo é 23 e a razão é – 6, a posição ocupada pelo elemento – 13 é:
Alternativa B
A fórmula do termo geral de uma PA é:
an = a1 + (n – 1)r
an é o termo geral
n é a posição ocupada pelo termo em questão
r é a razão da PA
a1 é o primeiro termo da progressão
Substituindo os valores dados no exercício na fórmula acima, teremos:
– 13 = 23 + (n – 1)·(– 6)
– 13 = 23 – 6n + 6
6n = 23 + 6 + 13
6n = 36 + 6
6n = 42
n = 42
6n = 7
O número – 13 ocupa a 7ª posição.
-
Questão 2
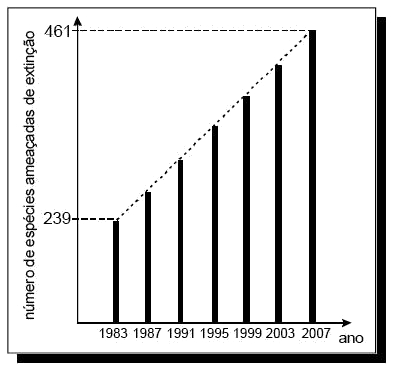
(Enem) O gráfico, obtido a partir de dados do Ministério do Meio Ambiente, mostra o crescimento do número de espécies da fauna brasileira ameaçadas de extinção. Se mantida, pelos próximos anos, a tendência de crescimento mostrada no gráfico, o número de espécies ameaçadas de extinção em 2011 será igual a:
Alternativa C
Observando o crescimento no gráfico, podemos concluir que ele é linear. Assim, a cada intervalo de quatro anos o número de espécies ameaças de extinção cresce de forma igual ao intervalo anterior.
Dessa forma, de acordo com o gráfico, o crescimento pode ser compreendido como uma progressão aritmética (PA), na qual os termos são o números de espécie ameaçadas de extinção a cada quatro anos.
O primeiro termo dessa PA é 239, e o sétimo termo é 461.
Com esses dados, podemos usar a fórmula do termo geral da PA para encontrar sua razão.
an = a1 + (n – 1)r
461 = 239 + (7 – 1)r
461 = 239 + 6r
461 – 239 = 6r
222 = 6r
r = 222
6r = 37
Observe no gráfico que os períodos observados são dados de quatro em quatro anos. Assim, o próximo número de espécies ameaçadas de extinção já é relativo a 2011. Portanto, basta somar a razão ao último termo para encontrar a solução:
461 + 37 = 498
-
Questão 3
Qual é o centésimo primeiro termo de uma PA cujo primeiro termo é 107 e a razão é 6?
Alternativa D
Considerando que o primeiro termo é 107, a razão é 6, e procuramos o centésimo primeiro termo, podemos usar a fórmula do termo geral da PA para encontrá-lo.
a100 = 107 + (101 – 1)·6
a100 = 107 + 100·6
a100 = 107 + 600
a100 = 707
-
Questão 4
Qual é a posição do termo 109 em uma PA de razão 3, cujo primeiro termo é igual a 10?
Alternativa E
Sabendo que o primeiro termo é 10, o último é 109 e a razão é 3, basta usar a fórmula do termo geral para encontrar a posição do termo 109:
an = a1 + (n – 1)r
109 = 10 + (n – 1)3
109 = 10 + 3n – 3
109 – 10 + 3 = 3n
102 = 3n
n = 102
3n = 34