Exercícios sobre Transformações Trigonométricas
Utilizando as transformações trigonométricas, mostre que sen 3a = 3 * sen a – 4 * sen3 a.
sen 3a = sen (2a + a) = sen 2a * cos a + sen a + cos 2a =
2 * sen a * cos a * cos a + sen a * (cos²a – sen² a) =
2 * sen a * cos² a + sen a * cos² a – sen³ a =
3 * sen a * cos² a – sen³ a =
3 * sen a * (1 – sen² a) – sen³ a =
3 * sen a – 3 * sen³ a – sen a =
3 * sen a – 4 * sen³ a
Calcule sen 2a sabendo que sen a – cos a = 2/5.
.gif)
Através dos cálculos verificamos que o sen 2a é igual a 21/25.
Demonstre a relação verdade da identidade trigonométrica 
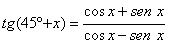
.gif)
(Fuvest-SP)
Qual o valor de (tg10º + cotg10º) * sen 20º ?
.gif)
O valor de (tg10º + cotg10º) * sen 20º é igual a 2.
(MACK-SP)
Qual o valor simplificado da expressão y = cos 80º + cos 40º – cos 20º ?
.gif)
O valor da expressão y = cos 80º + cos 40º – cos 20º corresponde a 0.
(Unifor-CE)
Lembrando que cos 75º = cos (45º + 30º), determine o valor de cos 2 985º.
.gif)
