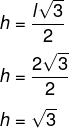Exercícios sobre triângulo equilátero
Esta lista de exercícios traz questões sobre os triângulos equiláteros, aqueles que possuem todos os lados congruentes, o que faz com que eles tenham propriedades únicas.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
O triângulo é o polígono que possui a menor quantidade de lados e ângulos, sendo um dos polígonos mais estudados, com uma vasta aplicação em problemas cotidianos. Existem algumas classificações para o triângulo, e uma delas é a de triângulo equilátero. Um triângulo é definido como triângulo equilátero quando
A) ele possuir todos os ângulos congruentes, ou seja, ângulos com a mesma medida.
B) ele possuir pelo menos dois lados congruentes.
C) ele possuir os lados diferentes mais proporcionais.
D) ele possuir todos os ângulos internos agudos.
E) ele possui todos os três lados congruentes.
Alternativa E. Um triângulo é considerado equilátero quando ele possui todos os seus lados congruentes.
-
Questão 2
Um triângulo equilátero possui altura igual a 4√3 cm, então, o perímetro desse polígono é de:
A) 4 cm
B) 8 cm
C) 16 cm
D) 24 cm
E) 32 cm
Alternativa D
Primeiro encontraremos o comprimento do lado do triângulo:
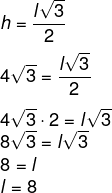
Agora que encontramos o comprimento do lado, é possível calcular o perímetro.
P = 3l
P = 3 · 8
P = 24 cm
-
Questão 3
Durante a medição de uma região para extração de minerais, foi identificada uma área de 435,2 m², limitada por um triângulo equilátero, que possui grande potencial para extração de ferro e outros metais. Utilizando √3 = 1,7, podemos afirmar que o comprimento de cada lado dessa região é de:
A) 32 m
B) 24 m
C) 16 m
D)12 m
E) 8 m
Alternativa A
Utilizando a fórmula da área de um triângulo equilátero, encontraremos o comprimento do seu lado, para, posteriormente, encontrarmos o perímetro.
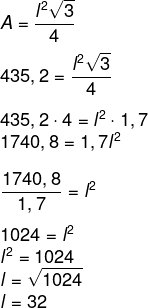
-
Questão 4
Na imagem a seguir, está representado um triângulo equilátero:
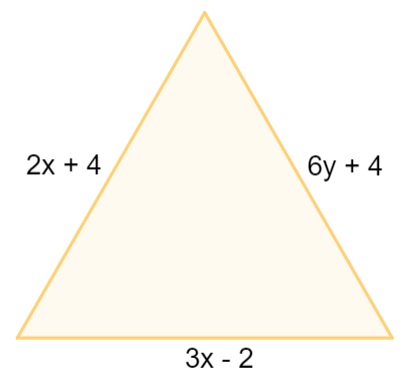
Analisando a imagem, podemos afirmar que o valor da soma x + y é igual a:
A) 2
B) 6
C) 8
D) 10
E) 11
Alternativa C
Como o triângulo é equilátero, podemos igualar os seus lados. Começando pelos lados que possuem a mesma variável x, temos que:
3x – 2 = 2x + 4
3x – 2x = 4 + 2
x = 6
Encontrado o valor de x, a medida de um lado desse triângulo é igual a:
2x + 4
2 · 6 + 4
12 + 4
16 cm
Então, analisando o lado que possui variável y, temos que:
6y + 4 = 16
6y = 16 – 4
6y = 12
y = 12 : 6
y = 2
Por fim, a soma:
x + y = 6 + 2 = 8
-
Questão 5
Sobre os triângulos equiláteros, julgue as afirmativas a seguir:
I → Todo triângulo equilátero possui ângulos internos medindo 60º.
II → Um triângulo equilátero não pode ser retângulo.
III → Todo triângulo acutângulo é também equilátero.
Marque a alternativa correta:
A) Somente a afirmativa I está incorreta.
B) Somente a afirmativa II está incorreta.
C) Somente a afirmativa III está incorreta.
D) Todas as afirmativas estão corretas.
Alternativa C
I → Verdadeira
Quando dividimos 180º por 3, encontramos 60º, isso significa que cada ângulo do triângulo equilátero de fato mede 60º.
II → Verdadeira
Como cada ângulo do triângulo equilátero mede 60º, então, ele é sempre acutângulo, o que faz com que ele nunca seja retângulo.
III → Falsa
Todo triângulo equilátero é acutângulo, mas nem todo triângulo acutângulo é equilátero. É possível construir um triângulo que seja acutângulo sem ser equilátero.
-
Questão 6
Analisando o triângulo a seguir, a área desse polígono é de:
(Use √3 = 1,7)
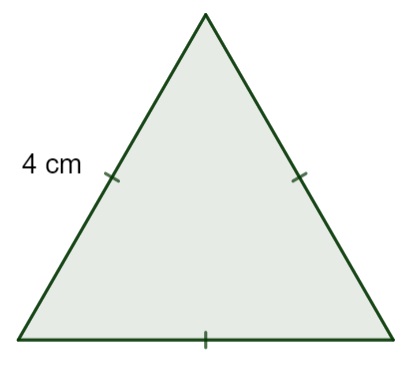
A) 5,5 cm²
B) 5,8 cm²
C) 6,4 cm²
D) 6,8 cm²
E) 9,2 cm²
Alternativa D
Utilizando a fórmula da área de um triângulo equilátero, temos que:
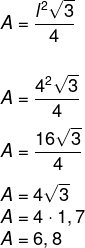
-
Questão 7
Um triângulo equilátero possui perímetro igual a 12 cm, então, podemos afirmar que a sua altura é igual a:
A) 2√3 cm
B) 4√3 cm
C) 8√3 cm
D) 2 cm
E) 4 cm
Alternativa A
Com o perímetro, é possível encontrar o comprimento do lado desse polígono.
P = 3l
12 = 3l
12 : 3 = l
l = 4
Sabemos que o lado é 4, basta então substituir na fórmula da altura:
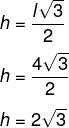
-
Questão 8
(Fuvest) Na figura, os segmentos AC e DE são paralelos entre si e perpendiculares ao segmento CD; o ponto B pertence ao segmento AC; F é o ponto médio do segmento AB; e ABE é um triângulo equilátero. Além disso, o segmento BC mede 10 unidades de comprimento e o segmento AE mede 6 unidades de comprimento.
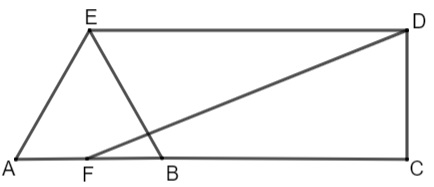
A medida do segmento DF, em unidades de comprimento, é igual a:
A) 14
B) 15
C) 16
D) 17
E) 18
Alternativa A
Colocando as informações importantes na imagem, sabemos que o triângulo possui lados medindo 6 cm. Como F é ponto médio, então, FB mede 3 e AF mede 3. Além disso, note que a altura do triângulo equilátero é igual ao comprimento DC. Podemos destacar também o triângulo FCD, que é retângulo, com a hipotenusa DF.
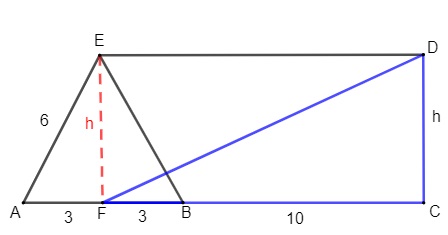
Queremos o valor de DF. Analisando o triângulo FCD, ele possui hipotenusa DF, logo, vamos calcular o valor de h e depois aplicar o teorema de Pitágoras para encontrar o comprimento DF.
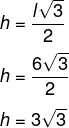
O lado FC mede 13 cm, h mede 3√3, então, pelo teorema de Pitágoras, temos que:
DF² = 13² + (3√3)²
DF² = 169 + 9 · 3
DF² = 169 + 27
DF² = 196
DF = √196
DF = 14
-
Questão 9
Para ladrilhar a área de lazer de um condomínio, foram utilizadas cerâmicas com 0,5 m² de área cada. Sabendo que a área de lazer possui o formato de um triângulo equilátero de 6 metros de lado, a quantidade de cerâmicas mínima necessária para cobrir toda a área de lazer é: (Use √3 = 1,7)
A) 15
B) 16
C) 31
D) 32
E) 35
Alternativa C
Primeiro calcularemos a área do triângulo equilátero:
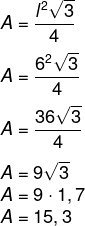
Como a área a ser ladrilhada possui 15,3 m², para calcular a quantidade de ladrilhos necessária, basta dividir 15,3 : 0,5 = 30,6.
Dessa forma, serão necessários 31 ladrilhos no mínimo.
-
Questão 10
Um triângulo equilátero possui perímetro igual a 30√3 metros, então, podemos afirmar que a altura desse triângulo é igual a:
A) 10 m
B) 15 m
C) 18 m
D) 22 m
E) 30 m
Alternativa B
Sabemos que o perímetro do triângulo é 3l, então, temos que:
3l = 30√3
l = 30√3 : 3
l = 10√3 cm
Agora calcularemos a altura utilizando a fórmula da altura do triângulo equilátero.
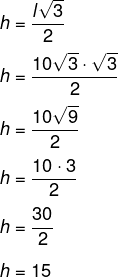
-
Questão 11
(Vunesp) O quadrado da altura de um triângulo equilátero é exatamente 300. O perímetro desse triângulo, em uma determinada unidade de medida, é:
A) 60
B) 50
C) 30
D) 20
E) 10
Alternativa A
Sabemos que h² = 300, então, temos que:
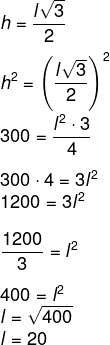
Como o lado mede 20, então, o perímetro é:
P = 3l
P = 3 · 20
P = 60
-
Questão 12
Sobre o triângulo equilátero, julgue as afirmativas a seguir:
I → Se um ângulo interno mede 60º, então, o triângulo é equilátero.
II → Um triângulo que possui os três congruentes é um triângulo equilátero.
III → O triângulo equilátero de lado 2 cm possui altura medindo √3 cm.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa A
I → Falsa
Se um ângulo mede 60º, não quer dizer que os demais medem 60º, logo, não podemos afirmar que esse triângulo é equilátero.
II → Verdadeira
Essa é a definição de triângulo equilátero.
III → Verdadeira
Se o lado mede 2, então, temos que: