Exercícios sobre triângulo isósceles
Existem duas maneiras de classificar um triângulo, uma delas é analisando os seus lados e a outra é analisando os seus ângulos. Quando classificamos o triângulo analisando os seus lados, ele é conhecido como isósceles quando:
A) possui todos os lados congruentes.
B) possui todos os lados não congruentes.
C) possui dois lados congruentes.
D) possui um dois lados perpendiculares.
Alternativa C
O triângulo é classificado como isósceles se ele possuir dois lados congruentes.
Um triângulo isósceles possui o ângulo da base medindo x + 20º e 2x – 8º, então, o ângulo do vértice desse triângulo mede:
A) 28°
B) 48°
C) 64°
D) 84°
E) 96°
Alternativa D
Como o triângulo é isósceles, os ângulos da base são congruentes, assim, temos que:
2x – 8° = x + 20°
2x – x = 20° + 8°
x = 28°
Sabendo que x = 28°, então, calculando a medida do ângulo da base, temos:
x + 20° = 28° + 20° = 48°
Como queremos o ângulo do vértice, o qual chamaremos de y, então, temos que:
y + 48° + 48° = 180°
y = 180° – 48° – 48°
y = 84°
Um triângulo isósceles ABC de base AB possui base medindo 26 cm e um dos seus lados oblíquos com 12 cm, então, podemos afirmar que o perímetro desse triângulo é de:
A) 20 cm
B) 24 cm
C) 26 cm
D) 48 cm
E) 50 cm
Alternativa E
Como esse triângulo é isósceles de base AB, os lados AC e BC são congruentes, e, se um dos seus lados oblíquos mede 12 cm, consequentemente, o outro lado também possui essa medida, então, seu perímetro será de:
P = 12 + 12 + 26
P = 50 cm
Um triângulo isósceles possui lados oblíquos medindo 10 cm, e base medindo 12 cm, então podemos afirmar que a área desse triângulo é igual a:
A) 30 cm²
B) 35 cm²
C) 42 cm²
D) 48 cm²
E) 50 cm²
Alternativa D
Para calcular a área desse triângulo, é necessário traçar a sua altura. Em um triângulo isósceles, a altura é a mediana da sua base, como na imagem a seguir:
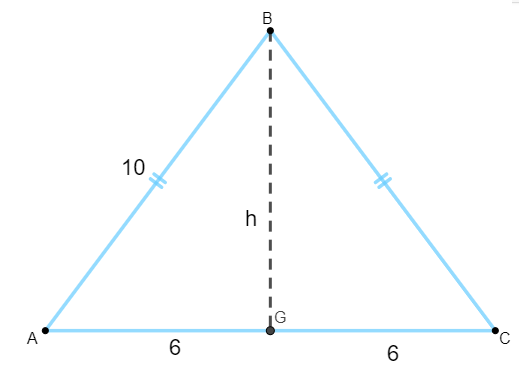
Então, para calcular a altura h, basta aplicar o teorema de Pitágoras.
10² = 6² + h²
100 = 36 + h²
100 – 36 = h²
84 = h²
h = √84
h = 8
Conhecendo a altura, sabemos que a área é o produto da base pela altura dividido por 2.
A = (12 · 8) : 2
A = 96 : 2
A = 48 cm²
Sobre o triângulo isósceles, podemos afirmar que:
I- Um triângulo isósceles pode ser acutângulo.
II- Um triângulo isósceles pode ser obtusângulo.
III- Um triângulo isósceles pode ser retângulo.
Analisando as afirmativas, marque a correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa D
I- Um triângulo isósceles pode ser acutângulo. (verdadeira)
Existe triângulo isósceles que é acutângulo, e ele deve possuir três ângulos agudos.
II- Um triângulo isósceles pode ser obtusângulo. (verdadeira)
Um triângulo isósceles pode ter o ângulo do vértice obtuso, logo, ele pode ser obtusângulo.
III- Um triângulo isósceles pode ser retângulo. (verdadeira)
Se os ângulos da base forem de 45°, teremos um triângulo isósceles e retângulo ao mesmo tempo.
Todas as afirmativas são verdadeiras.
O triângulo ABC, a seguir, é isósceles de perímetro igual a 190 cm:
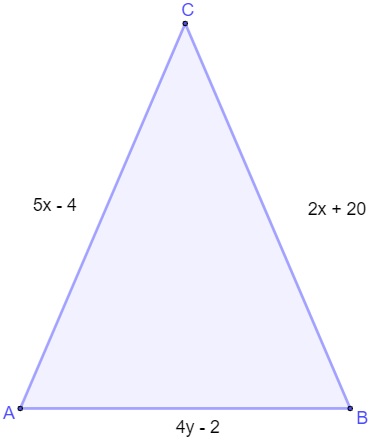
Sabendo que AB é a sua base, analisando esse triângulo, podemos afirmar que x – y é igual a:
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa B
Primeiro encontraremos o valor de x, como ele é isósceles, temos que:
5x – 4 = 2x + 20
5x – 2x = 20 + 4
3x = 24
x = 24 : 3
x = 8
Sabendo que x = 8, então, substituindo esse valor em um dos lados, encontraremos o comprimento dos lados oblíquos:
2x + 20
2 · 8 + 20
16 + 20
36 cm
Agora, com a informação do perímetro, encontraremos o valor de y:
36 + 36 + 4y – 2 = 90
70 + 4y = 90
4y = 90 – 70
4y = 20
y = 20 : 4
y = 5
Desse modo, a diferença entre x e y:
8 – 5 = 3
Um triângulo possui lados medindo 2x – 3, x + 6 e 2x + 2. Sabendo que esse triângulo possui perímetro igual a 50 cm, podemos afirmar que ele é:
A) escaleno
B) isósceles
C) equilátero
D) equiângulo
E) trapézio
Alternativa B
Para encontrar o valor de x, temos que:
2x – 3 + x + 6 + 2x + 2 = 50
5x + 5 = 50
5x = 50 – 5
5x = 45
x = 45 : 5
x = 9
Sabendo que x = 9, encontraremos o comprimento dos lados:
2x – 3 = 2 · 9 – 3 = 18 – 3 = 15
x + 6 = 9 + 6 = 15
2x + 2 = 2 · 9 + 2 = 18 + 2 = 20
Note que ele possui dois lados congruentes, logo, esse triângulo é isósceles.
Analisando o triângulo a seguir, o valor do ângulo BAC é:
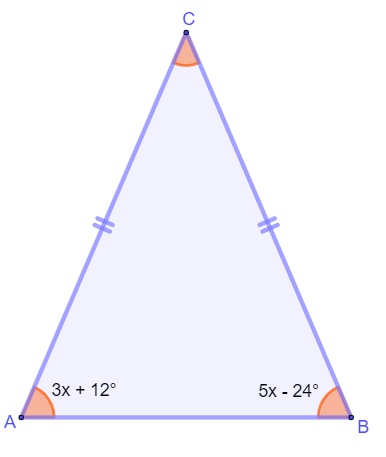
A) 18°
B) 36°
C) 50°
D) 66°
E) 72°
Alternativa D
Pela imagem, é possível perceber que AC é congruente a BC, então, esse triângulo é isósceles, logo, os ângulos da base são congruentes.
5x – 24° = 3x + 12°
5x – 3x = 12 + 24
2x = 36
x = 36 : 2
x = 18
Então, o ângulo BAC mede:
3 · 18 + 24 = 66°
Sobre o triângulo isósceles, julgue as afirmativas a seguir:
I → A bissetriz do vértice do triângulo isósceles é também a sua mediana.
II → O triângulo isósceles é um caso particular do triângulo acutângulo.
III → O triângulo isósceles possui todos os lados congruentes.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são verdadeiras.
E) Todas as afirmativas são falsas.
Alternativa A
I → A bissetriz do vértice do triângulo isósceles é também a sua mediana. (verdadeira)
Em um triângulo isósceles, a altura, a bissetriz e a mediana do vértice coincidem.
II → O triângulo isósceles é um caso particular do triângulo acutângulo. (falsa)
O triângulo isósceles pode ser retângulo ou obtusângulo também.
III → O triângulo isósceles possui todos os lados congruentes. (falsa)
Para ser isósceles, basta que o triângulo tenha dois lados congruentes.
Qual é a altura de um triângulo isósceles que possui lados oblíquos medindo 15 cm e base igual a 18 cm?
A) 12 cm
B) 10 cm
C) 8 cm
D) 6 cm
E) 4 cm
Alternativa A
Em um triângulo isósceles, quando traçamos a altura, ela sempre dividirá a base ao meio, como na imagem a seguir:
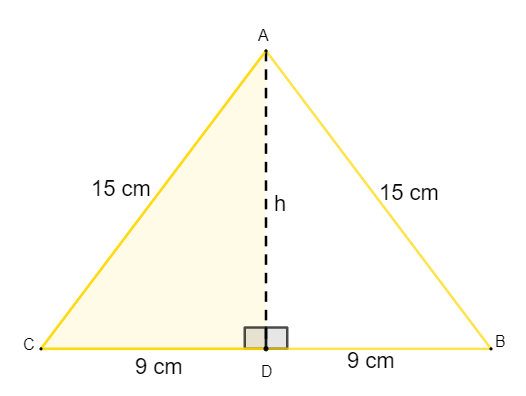
Aplicando o teorema de Pitágoras no triângulo ADC, temos que:
15² = 9² + h²
225 = 81 + h²
225 – 81 = h²
144 = h²
h = √144
h = 12 cm
Um triângulo isósceles possui área igual a 12 cm². Sabendo que a sua base mede 8 cm, então, o perímetro desse triângulo é de:
A) 18 cm
B) 16 cm
C) 14 cm
D) 12 cm
E) 10 cm
Alternativa A
Como a área é igual a 12 cm², encontraremos a altura desse triângulo:
A = (b · h) : 2
12 = (8 · h) : 2
12 · 2 = 8h
24 = 8h
h = 24 : 8
h = 3
Sabendo que a altura é igual a 3, para encontrar o comprimento do lado oblíquo x, usaremos a metade do comprimento da base à altura e o próprio lado oblíquo, os quais possuem uma relação pitagórica:
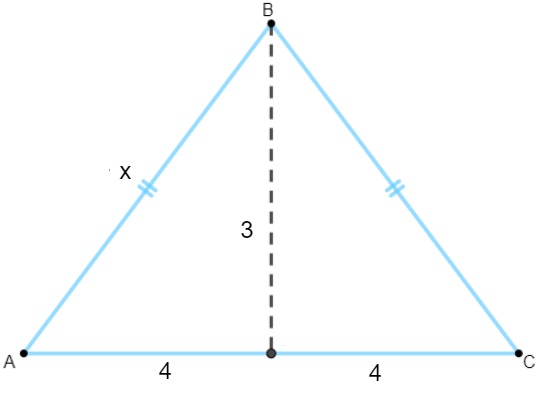
Dessa forma, temos que:
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
Sabendo que x = 5, o perímetro é de:
P = 5 + 5 + 8 = 18 cm
(Cefet SC) Num triângulo isósceles, cada ângulo da base mede o dobro da medida do ângulo do vértice. A medida do ângulo do vértice é:
A) 36°
B) 72°
C) 50°
D) 40°
E) 80°
Alternativa A
Seja x o ângulo do vértice, então os ângulos da base medem 2x cada. Sabemos que a soma dos ângulos internos de um triângulo é 180º, então, temos que:
x + 2x + 2x = 180º
5x = 180º
x = 180º : 5
x = 36º
