Exercícios sobre triângulo retângulo
Esta lista de exercícios contém questões envolvendo os principais conceitos sobre o triângulo retângulo, as suas propriedades, o teorema de Pitágoras e a trigonometria.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Marque a alternativa que define corretamente o que é um triângulo retângulo.
A) Um triângulo é retângulo quando ele possui todos os seus ângulos retos.
B) Um triângulo é retângulo quando ele está inscrito dentro de um retângulo.
C) Um triângulo é retângulo quando ele possui um ângulo de 90°.
D) Um triângulo é retângulo quando ele possui um ângulo maior que 90°.
E) Um triângulo é retângulo quando ele possui todos os lados congruentes.
-
Questão 2
Analisando o triângulo retângulo a seguir, qual deve ser o valor de x para que o seu perímetro seja igual a 40?
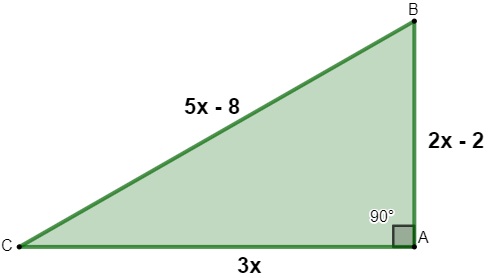
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa D
Sabemos que o perímetro é a soma de todos os lados de um triângulo, então, temos que:
P = 3x + 5x – 8 + 2x – 2 = 40
10x – 10 = 40
10x = 40 + 10
10x = 50
x = 50 : 10
x = 5
-
Questão 3
Analise o triângulo a seguir:
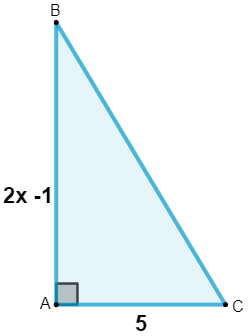
Sabendo que a sua área é igual a 30 metros, então, o valor de x é igual a:
A) 4,0 m
B) 5,5 m
C) 6,0 m
D) 6,5 m
E) 7,0 m
Alternativa D
Sabemos que o produto entre os catetos dividido por 2 é igual à área do triângulo, então, temos que:
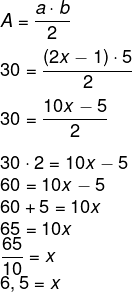
-
Questão 4
Sabendo que as medidas foram dadas em centímetros, o perímetro do triângulo retângulo a seguir é igual a:
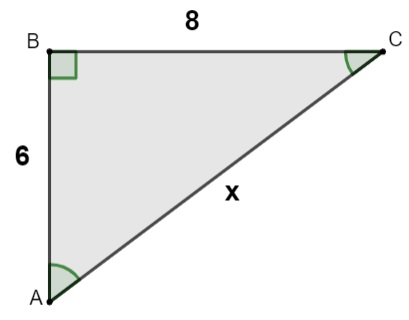
A) 10 cm
B) 14 cm
C) 16 cm
D) 24 cm
E) 48 cm
Alternativa D
Primeiro, usamos o teorema de Pitágoras para encontrar o valor de x:
x² = 6² + 8²
x² = 36 + 48
x² = 100
x = √100
x = 10 cm
Agora, calcularemos o perímetro:
P = 10 + 8 + 6 = 24 cm
-
Questão 5
(Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de
A) 6√3 m.
B) 12 m.
C) 13,6 m.
D) 9√3 m.
E) 18 m.
Alternativa E
Fazendo a ilustração da situação:
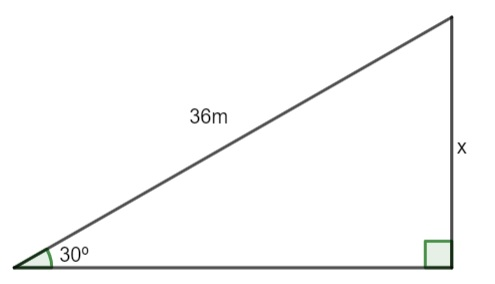
Note que a altura é o cateto oposto do ângulo de 30°, e conhecemos o valor da hipotenusa do triângulo, então, aplicaremos o seno de 30°:
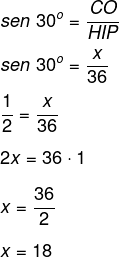
Dessa forma, a altura será de 18 metros.
-
Questão 6
(Enem) As torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha. A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB). Essas torres são um bom exemplo de um prisma oblíquo de base quadrada, e uma delas pode ser observada na imagem.

Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço
A) menor que 100 m².
B) entre 100 m² e 300 m².
C) entre 300 m² e 500 m².
D) entre 500 m² e 700 m².
E) maior que 700 m².
Alternativa E
O segmento AB divide a face do prédio em dois triângulos retângulos, sabendo que o ângulo B é igual a 15º e conecendo o cateto adjacente a ele, é possível calcular o tamanho da base utilizando a tangente.
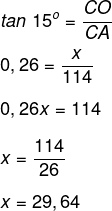
Como a base é um quadrado, a sua área será igual ao lado ao quadrado, então, temos que:
A = 29,64² = 878,53
-
Questão 7
Analise o triângulo a seguir sabendo que a medida do seu lado é dada em metros.
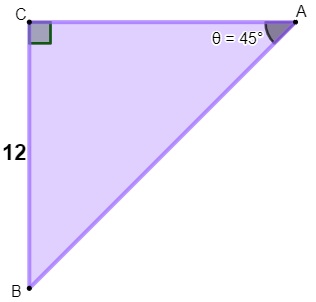
A área desse triângulo é igual a:
A) 12 m²
B) 25 m²
C) 56 m²
D) 64 m²
E) 72 m²
Alternativa E
Podemos afirmar que esse triângulo retângulo é isósceles, pois, se um ângulo mede 45° e o outro mede 90º, seja x a medida do outro ângulo, temos que:
x + 45° + 90° = 180°
x = 180° – 90° – 45°
x = 45°
Como o triângulo é isósceles, sabemos que o lado AC também mede 12 m, então, calculando a área, temos que:
A = 12 · 12 : 2
A = 144 : 2
A = 72 m²
-
Questão 8
Um triângulo é considerado retângulo quando um dos seus ângulos for reto. Esse tipo de triângulo é estudado amplamente. Sobre ele, julgue as afirmativas a seguir:
I → Um triângulo retângulo pode ser escaleno.
II → Um triângulo retângulo pode ser isósceles.
III → Um triângulo retângulo pode ser equilátero.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa C
I → Um triângulo retângulo pode ser escaleno. (verdadeira)
Existem vários casos de triângulo retângulo que possui todos os lados com medidas diferentes, logo, um triângulo retângulo pode ser também escaleno.
II → Um triângulo retângulo pode ser isósceles. (verdadeira)
É possível que um triângulo retângulo seja isósceles, para isso, os outros dois ângulos precisam ser de 45º cada.
III → Um triângulo retângulo pode ser equilátero. (falsa)
O triângulo equilátero possui todos os ângulos internos medindo 60º, logo, ele não pode ser retângulo.
-
Questão 9
Durante a coleta de dados sobre o desmatamento, foi analisada uma região da Amazônia que forma um triângulo retângulo com catetos medindo 2 km e 1,5 km e hipotenusa medindo 2,5 km. Então, analisando essa região, podemos afirmar que a área desmatada foi de:
A) 1,2 km²
B) 1,5 km²
C) 2,0 km²
D) 5,0 km²
E) 6,5 km²
Alternativa B
Para saber a área de um triângulo retângulo, calculamos o produto entre os seus catetos e o dividimos por 2. Assim, temos que:
A = (2 · 1,5) : 2
A = 3 : 2
A = 1,5 km²
-
Questão 10
Num terreno retangular, foi traçada a diagonal dividindo-o em dois triângulos iguais, como na imagem a seguir.
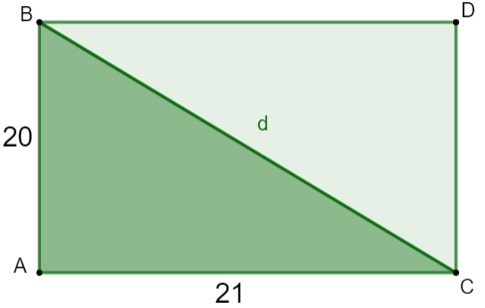
Analisando esse terreno, e sabendo que as suas medidas foram dadas em metros, podemos afirmar que o comprimento da sua diagonal é igual a:
A) 25 metros
B) 26 metros
C) 27 metros
D) 29 metros
E) 30 metros
Alternativa D
Analisando o triângulo ABC, sabemos que ele é retângulo, logo, podemos aplicar o teorema de Pitágoras, então, temos que:
d² = 20² + 21²
d² = 400 + 441
d² = 841
d = √841
d = 29
-
Questão 11
(IFG 2017) Teodolito é um instrumento de precisão para medir ângulos horizontais e ângulos verticais, utilizado em trabalhos de construção. Uma empresa foi contratada para pintar um edifício de quatro andares. Para descobrir a área total a ser pintada, ela precisa descobrir a altura do edifício. Uma pessoa posiciona o instrumento a 1,65 metros de altura, encontrando um ângulo de 30°, conforme mostra a figura. Supondo que o teodolito esteja distante 13√3 metros do edifício, qual a altura, em metros, do prédio a ser pintado?
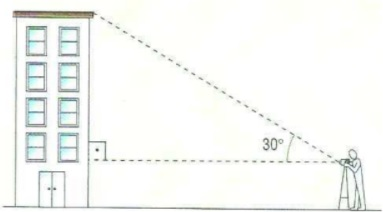
A) 11,65
B) 12,65
C) 13,65
D) 14,65
E) 15,65
Alternativa D
Como queremos encontrar o cateto oposto ao ângulo de 30º e sabemos que a distância 13√3 (do teodolito até o prédio) é o cateto adjacente ao ângulo de 30º, então, usaremos a tangente:
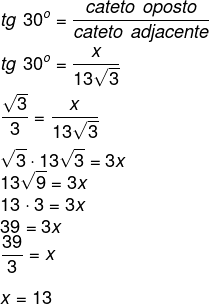
Agora, somaremos 13 + 1,65 = 14,65 metros de altura.
-
Questão 12
(IFG 2019) Considere que o tamanho de uma televisão, dado em polegadas, corresponde ao comprimento da sua diagonal e que, no caso de televisores de tamanho normal, a largura e a altura seguem, ordenadamente, a relação 4:3. Observe a figura abaixo e considere 1 polegada = 2,5 cm.

Com relação a uma televisão plana de 40 polegadas, é correto afirmar que sua largura e sua altura são, respectivamente:
A) 60 cm e 45 cm
B) 80 cm e 60 cm
C) 64 cm e 48 cm
D) 68 cm e 51 cm
Alternativa B
Se a proporção dos lados é de 4:3, então a largura mede 4x e a altura mede 3x. Note que 40” é a medida da diagonal da televisão e que a diagonal divide a televisão em dois triângulos retângulos, logo, podemos aplicar o teorema de Pitágoras.
(4x)² + (3x)² = 40²
16x² + 9x² = 1600
25x² = 1600
x² = 1600 : 25
x² = 64
x = √64
x = 8
Como os lados medem 4x e 3x, então, temos que:
4x → 4 · 8 = 32”
3x → 3 · 8 = 24”
Como 1 polegada corresponde a 2,5 cm, então:
32 · 2,5 = 80 centímetros
24 · 2,5 = 60 centímetros