Exercícios sobre tronco de cone
Determine o volume de um tronco de cone com raio da base inferior de 4 cm, raio da base superior de 2 cm e altura de 6 cm.
A) 12π cm3
B) 24π cm3
C) 36π cm3
D) 56π cm3
E) 64π cm3
Alternativa D
O volume do tronco de cone é dado por:
\(V=\frac{\pi h(R^2+r^2+rR)}{3}\)
Substituindo os dados fornecidos pelo exercício, temos
\(V=π6\frac{(42+22+4⸳2)}3=2π16+4+8=56π cm3\)
Calcule a área da superfície lateral de um tronco de cone com raio da base inferior de 7 cm, raio da base superior de 5 cm e geratriz de 10 cm.
A) 120π cm2
B) 160π cm2
C) 200π cm2
D) 240π cm2
E) 320π cm2
Alternativa A
A área da superfície lateral é dada por:
\(A=\pi g(r+R)\)
Substituindo os valores dados pelo exercício na expressão acima, temos:
\(A=\pi10\left(5+7\right)=120{\pi cm}^2\)
Encontre o raio da base superior de um tronco de cone com volume de 105π cm³, raio da base inferior de 6 cm e altura de 5 cm:
A) 2 cm
B) 3 cm
C) 4 cm
D) 5 cm
E) 6 cm
Alternativa B
O volume do tronco de cone é dado por:
\(V=\frac{\pi h(R^2+r^2+rR)}{3}\)
Substituindo os dados fornecidos pelo exercício, temos:
\(105\pi=\frac{π5(62+r2+r⸳6)}3\)
\(63=36{+r}^2+r⸳6\)
\(r^2+6r-27=0\)
As raízes dessa equação são -9 e 3.
Como raio é um valor positivo, temos que \(r=3\ cm\).
Um tronco de cone tem raio da base inferior de 10 cm, raio da base superior de 4 cm e altura de 8 cm. Calcule sua área total (incluindo as bases).
A) 100π cm2
B) 146π cm2
C) 256π cm2
D) 326π cm2
E) 360π cm2
Alternativa C
- A área da base superior é \(Ainferior=\pi4^2=16{\pi\ cm}^2\).
- A área da base inferior é \(Asuperior=\pi{10}^2=100{\pi\ cm}^2\).
- A geratriz é dada por \(g^2=h^2+{(R-r)}^2\).
\(g^2=8^2+{(10-4)}^2=64+36=100\)
Logo, a geratriz tem 10 cm.
A área da superfície lateral é dada por \(A=\pi g(r+R)\).
Substituindo os valores encontrados e dados pelo exercício na expressão acima, temos:
\(A=\pi10\left(10+4\right)=140{\pi\ cm}^2\)
Área total é a soma das áreas acima.
\(A_{total}=16\pi+100\pi+140\pi=256\pi\ {cm}^2\)
Um tronco de cone é formado pela retirada de um cone menor de um cone maior. O cone maior tem raio da base de 8 cm e altura de 12 cm, enquanto o cone menor tem raio da base de 4 cm e altura de 6 cm. Calcule o volume do tronco de cone resultante.
A) 128π cm3
B) 224π cm3
C) 316π cm3
D) 356π cm3
E) 464π cm3
Alternativa B
O volume do tronco de cone é dado por \(V=\frac{\pi h(R^2+r^2+rR)}{3}\).
Sabemos que a altura do tronco de cone é dada pela diferença entre as alturas dos cones, logo essa altura é igual a \(h=12-6=6\ cm\).
Substituindo os dados fornecidos pelo exercício, temos:
\(V=\frac{π6(82+42+8⸳4)}3=2π64+16+32=224π cm3\)
Se um tronco de cone tem área da superfície lateral de 260π cm², raio da base inferior de 4 cm e raio da base superior igual a 6 cm, encontre a altura do tronco de cone.
A) 18,7 cm
B) 25,98 cm
C) 27,4 cm
D) 23,3 cm
E) 29,5 cm
Alternativa B
A área da superfície lateral é dada por \(A=\pi g(r+R)\).
Substituindo os valores encontrados e dados pelo exercício na expressão acima, temos:
\(260\pi=\pi g\left(4+6\right)\)
Logo a geratriz tem 26 cm.
A geratriz é dada por \(g^2=h^2+{(R-r)}^2\):
\({26}^2=h^2+{(6-4)}^2\)
\(676=h^2+4\)
\(h^2=672\)
\(h=\sqrt{672}\)
\(h\approx25,98\)
Um tronco de cone tem raio da base superior igual a 8 cm, raio da base inferior igual a 4 cm e altura de 10 cm. Determine o volume desse tronco de cone. (Adote π=3)
A) 720 cm3
B) 620 cm3
C) 1520 cm3
D) 3360 cm3
E) 1120 cm3
Alternativa E
O volume do tronco de cone é dado por \(V=\frac{\pi h(R^2+r^2+rR)}{3}\).
Substituindo os dados fornecidos pelo exercício, temos:
\(V=\frac{3\cdot10(8^2+4^2+8\cdot4)}3=10(64+16+32)=1120 cm^3\)
Se um tronco de cone tem volume de 150π cm³, raio da base inferior de 5 cm e altura de 8 cm, qual é o raio da base superior?
A) 2,4
B) 3,1
C) 3,6
D) 4,1
E) 5,3
Alternativa C
O volume do tronco de cone é dado por \(V=\frac{\pi h(R^2+r^2+rR)}{3}\).
Substituindo os dados fornecidos pelo exercício, temos:
\(150\pi=\frac{\pi8(r^2+5^2+r5)}{3}\)
\(450=8r^2+200+40r\)
\(8r^2+40r-250=0\)
\(4r^2+20r-125=0\)
As raízes dessa equação são aproximadamente 3,6 e -8,6.
Como raio é um valor positivo, temos que r=3,6 cm.
Em uma construção civil, um tronco de cone de 10 m de altura tem raio da base menor igual a 4 m e raio da base maior igual a 6 m. Sabendo que o concreto custa R$ 200 por metro cúbico, calcule o custo total para preencher o tronco de cone. (Adote π=3)
A) R$ 120.000,00
B) R$ 144.000,00
C) R$ 152.000,00
D) R$ 172.000,00
E) R$ 192.000,00
Alternativa C
O volume do tronco de cone é dado por \(V=\frac{\pi h(R^2+r^2+rR)}{3}\).
Substituindo os dados fornecidos pelo exercício, temos:
\(V=\frac{3⸳10(62+42+6⸳4)}3=1036+16+24=760 m3\)
Logo, o custo total é \(760\cdot200=R$\ 152.000,00\).
Uma vela foi moldada na forma de um tronco de cone, com altura de 12 cm, raio da base menor de 2 cm e raio da base maior de 6 cm. Sabendo que essa vela derrete a uma razão de 2 cm3 por minuto, determine o tempo para ela estar completamente derretida. (Adote π=3)
A) 3 horas e 10 minutos
B) 4 horas e 12 minutos
C) 5 horas e 12 minutos
D) 6 horas e 10 minutos
E) 7 horas e 21 minutos
Alternativa C
O volume do tronco de cone é dado por \(V=\frac{\pi h(R^2+r^2+rR)}{3}\).
Substituindo os dados fornecidos pelo exercício, temos:
\(V=\frac{3⸳12(62+22+6⸳2)}3=12(36+4+12)=624 cm^3\)
Logo, o tempo gasto é de \(t=\frac{624}{2}=312\ minutos=5\ horas\ e\ 12\ minutos\).
Um tronco de cone tem altura de 9 cm, e a diferença entre os raios da base maior e menor é de 12 cm. Se a área da superfície lateral desse tronco é de 540π cm², encontre o raio da base maior.
A) 15 cm
B) 17 cm
C) 24 cm
D) 27 cm
E) 30 cm
Alternativa C
A área da superfície lateral é dada por \(A=\pi g(r+R)\):
\(540\pi=\pi g(r+R)\)
\(540=g(r+R)\)
O enunciado afirmou que \(R=r+12\), então substituindo temos que \(540=g(2r+12)\).
Sabemos que \(g^2=h^2+{(R-r)}^2\):
\(g^2=9^2+{(12)}^2=225\)
\(g=\sqrt{225}=15\ cm\)
\(Logo\ 540=15\left(2r+12\right)\)
\(540=30r+180\)
\(r=12\ cm\)
Logo, \(R=12+12=24\ cm\).
As figuras 1 e 2 são semelhantes. O volume da Figura 1 é 20 litros, e o raio de sua base menor é metade do raio da base menor da Figura 2. Determine o volume da Figura 2.
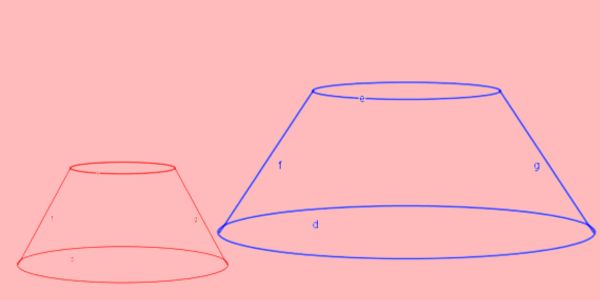
A) 10 litros
B) 40 litros
C) 80 litros
D) 160 litros
E) 320 litros
Alternativa D
A figura 1 possui volume igual a \( V1=\frac{\pi h(R^2+r^2+rR)}{3}\).
A figura 2 possui volume igual a \(V1=\frac{\pi2h((2{R)}^2+\left(2r\right)^2+2r2R)}{3}=8\frac{\pi h(R^2+r^2+rR)}{3}=8⸳20=160 litros\).
