Home
Exercícios de Matemática
Exercícios sobre volume da esfera

Exercícios sobre volume da esfera

Resolva esta lista de exercícios sobre volume da esfera e avalie seus conhecimentos sobre a medida do espaço ocupado por esse sólido. Publicado por: Raul Rodrigues de Oliveira

Imprimir

Questão 1

Uma esfera possui raio medindo 5 cm, então a medida do volume dessa esfera é igual a:

A) $500\pi\ cm^3$

B) $\frac{125}{3}\pi\ cm^3$

C) $250\pi\ cm^3$

D) $\frac{500}{3}\pi\ cm^3$

E) $700\pi\ cm^3$

Ver resposta

Resposta

Alternativa D

Calculando o volume da esfera, temos que:

$V=\frac{4}{3}\pi r^3$

$V=\frac{4}{3}\cdot\pi\cdot5^3$

$V=\frac{4}{3}\cdot\pi\cdot125$

$V=\frac{500}{3}\pi$

Questão 2

Uma esfera possui área medindo 36π m³, então podemos afirmar que a medida do seu diâmetro é igual a:

A) 3 m

B) 4 m

C) 6 m

D) 8 m

E) 9 m

Ver resposta

Resposta

Alternativa C

Sabemos que:

$V=\frac{4}{3}\pi r^3$

$36\pi=\frac{4}{3}\pi r^3$

$36\cdot3\pi=4\pi r^3$

$108\pi=4\pi r^3$

$\frac{108\pi}{4\pi}=r^3$

$27=r^3$

$\sqrt[3]{27}=r$

$3=r$

Se o raio mede 3, então o diâmetro mede 6 m.

Questão 3

Uma esfera com diâmetro de 12 cm está inscrita em um cubo. A diferença entre o volume do cubo e o volume da esfera é de:

(Use π = 3)

A) 1728 cm³

B) 1519 cm³

C) 1194 cm³

D) 989 cm³

E) 864 cm³

Ver resposta

Resposta

Alternativa E

A aresta do cubo é igual ao diâmetro da esfera, pois a esfera está inscrita no cubo. Calculando o volume do cubo, temos que:

$V_{cubo}={12}^3$

$V_{cubo}=1728\ cm^3$

Agora, calculando o volume da esfera:

$V_{esfera}=\frac{4}{3}\cdot\pi\cdot6^3$

$V_{esfera}=\frac{4}{3}\cdot3\cdot216$

$V_{esfera}=4\cdot216$

$V_{esfera}=864\ cm^3$

A diferença entre os volumes é:

$V = 1728 – 864 = 864$

Questão 4

Uma esfera possui a medida da sua área igual ao seu volume. Sabendo que a medida do seu raio foi dada em centímetros, então o comprimento do raio dessa esfera é igual a:

A) 1 cm

B) 2 cm

C) 3 cm

D) 4 cm

E) 5 cm

Ver resposta

Resposta

Alternativa C

Como o volume da esfera é igual à área:

$\frac{4}{3}\pi r^3=4\pi r^2$

$4\pi r^3=3\cdot4\pi r^2$

$4\pi r^3=12\pi r^2$

$\frac{r^3}{r^2}=\frac{12\pi}{4\pi}$

$r=3\$

Questão 5

Uma empresa possui um reservatório de gás no formato de uma esfera, com raio medindo R. Durante uma reforma nessa empresa, ficou decido que seria feito um novo reservatório, cujo raio mediria 80% do raio do reservatório anterior. Ao comparar o volume do novo reservatório, podemos afirmar que ele é:

A) 20,0% do volume do reservatório anterior.

B) 51,2% do volume do reservatório anterior.

C) 62,0% do volume do reservatório anterior.

D) 76,4% do volume do reservatório anterior.

E) 84,2% do volume do reservatório anterior.

Ver resposta

Resposta

Alternativa B

Calculando o volume do novo reservatório, temos que:

$V=\frac{4}{3}\pi\left(0,8R\right)^3$

$V=\frac{4}{3}\pi R^3\cdot0,512$

Note então que:

$V=\frac{4}{3}\pi R^3\cdot51,2%$

Podemos afirmar que o novo reservatório possui volume igual a 8% do volume do reservatório anterior.

Questão 6

Um frasco de perfume será fabricado de forma que caiba nele 256 ml de perfume. Qual deve ser a medida do raio desse frasco caso ele tenha formato de uma esfera? (Use π=3)

A) 1 cm

B) 2 cm

C) 3 cm

D) 4 cm

E) 5 cm

Ver resposta

Resposta

Alternativa D

Sabemos que 256 ml correspondem a 256 cm. Então temos que:

$V=\frac{4}{3}\pi r^3$

$256=\frac{4}{3}\cdot3\cdot r^3$

$256=4r^3$

$\frac{256}{4}=r^3$

$30=r^3$

$r=\sqrt[3]{64}$

$r=4\ cm$

Questão 7

Uma esfera está inscrita em um cubo cuja aresta mede 8 cm. Então podemos afirmar que a medida do volume dessa esfera é igual a:

(Use π = 3)

A) 128 cm³

B) 256 cm³

C) 384 cm³

D) 512 cm³

E) 638 cm³

Ver resposta

Resposta

Alternativa B

Como a aresta do cubo é igual a 8 cm, e a esfera está inscrita nesse cubo, então podemos afirmar que o diâmetro da esfera é igual a 8 cm, logo, o raio é igual a 4 cm. Calculando o volume da esfera, temos que:

$V=\frac{4}{3}\pi r^3$

$V=\frac{4}{3}\cdot\pi\cdot4^3$

$V=\frac{4}{3}\cdot3\cdot64$

$V=4\cdot64$

$V=256\ cm^3$

Questão 8

Dada uma esfera de raio R, se dobrarmos a medida desse raio, o volume da nova esfera em comparação com a esfera de raio medindo R será:

A) 2 vezes maior

B) 4 vezes maior

C) 6 vezes maior

D) 8 vezes maior

E) 10 vezes maior

Ver resposta

Resposta

Alternativa D

Seja V o volume da esfera de raio R, então temos que:

$V=\frac{4}{3}\pi r^3$

Como o novo raio é o dobro do anterior, então temos que:

$V_2=\frac{4}{3}\cdot\pi\cdot\left(2r^3\right)$

$V_2=\frac{4}{3}\pi\cdot8\cdot r^3$

$V_2=8\cdot\frac{4}{3}\pi r^3$

$V_2=8$

Então o volume novo é 8 vezes maior.

Questão 9

(Enem) Uma cozinheira produz docinhos especiais por encomenda. Usando uma receita-base de massa, ela prepara uma porção, com a qual produz 50 docinhos maciços de formato esférico, com 2 cm de diâmetro.

Um cliente encomenda 150 desses docinhos, mas pede que cada um tenha formato esférico com 4 cm de diâmetro.

A cozinheira pretende preparar o número exato de porções da receita-base de massa necessário para produzir os docinhos dessa encomenda.

Quantas porções da receita-base de massa ela deve preparar para atender esse cliente?

A) 2

B) 3

C) 6

D) 12

E) 24

Ver resposta

Resposta

Alternativa E

Considerando o raio 1, temos que:

$V=\frac{4}{3}\pi r^3$

$V=\frac{4}{3}\pi1^3$

$V=\frac{4}{3}\pi$

Sabemos que há 50 docinhos por porção, então temos que:

$50\cdot\frac{4}{3}\pi=\frac{200}{3}\pi$

Agora calcularemos o volume de doce pedido pelo cliente: 150 docinhos com 2 cm de raio.

$150\cdot\frac{4}{3}\pi r^3$

$150\cdot\frac{4}{3}\pi2^3$

$150\cdot\frac{4}{3}\pi\cdot8$

$150\cdot\frac{32}{3}\pi$

$\frac{4800}{3}\pi$

$1600\pi$

Dividindo pelo volume de cada porção, temos que:

$1600\pi:\frac{200}{3}\pi=1600\cdot\frac{3}{200}=8\cdot3=24$

Questão 10

(Enem) Uma indústria de perfumes embala seus produtos, atualmente, em frascos esféricos de raio R, com volume dado por $\frac{4}{3}\pi R^3$ . Observou-se que haverá redução de custos se forem utilizados frascos cilíndricos com raio da base $\frac{R}{3}$ cujo volume será dado por $\pi\left(\frac{R}{3}\right)^2\cdot h$ , sendo h a altura da nova embalagem. Para que seja mantida a mesma capacidade do frasco esférico, a altura do frasco cilíndrico (em termos de R) deverá ser igual a:

A) 2R

B) 4R

C) 6R

D) 9R

E) 12R

Ver resposta

Resposta

Alternativa E

Sabemos que o volume da esfera é igual ao volume do cilindro:

$\frac{4}{3}\pi R^3=\pi\left(\frac{R}{3}\right)^2\cdot h$

$\frac{4}{3}\pi R^3=\pi\frac{R^2}{9}\cdot h$

$4R^3=3\frac{R^2}{9}\cdot h\$

$4R^3=\frac{R^2}{3}h$

$4\cdot3R^3=R^2h$

$12R^3=R^2h$

$12R=h$

Questão 11

(Enem) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.

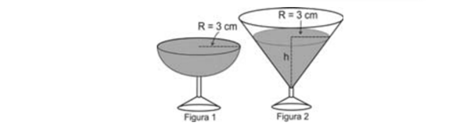
Ilustração de uma taça com formato de hemisfério ao lado de uma taça com formato de cone em uma questão do Enem sobre volume da esfera.

Considere:

$V_{esfera}=\ \frac{4}{3}\pi R^3\ e\ V_{cone}=\ \frac{1}{3}\pi R^2h\$

Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de

A) 1,33.

B) 6,00.

C) 12,00.

D) 56,52.

E) 113,04.

Ver resposta

Resposta

Alternativa B

Como o volume da esfera é $\frac{4}{3}\pi R^3$ , então o volume de um hemisfério será $\frac{4}{6}\pi R^3$ , logo, temos que:

$\frac{4}{6}\pi R^3=\frac{1}{3}\pi r^2h$

$\frac{4}{6}\pi\cdot3^3=\frac{1}{3}\pi\cdot3^2h$

$\frac{4}{6}\pi\cdot27=\frac{1}{3}\cdot\pi\cdot9h$

$\frac{108\pi}{6}=3\pi h$

$18\pi=\ 3\pi h$

$\frac{18\pi}{3\pi}=h$

$6=h$

Questão 12

(Enem) Peças metálicas de aeronaves abandonadas em aeroportos serão recicladas. Uma dessas peças é maciça e tem o formato cilíndrico, com a medida do raio da base igual a 4 cm e a da altura igual a 50 cm. Ela será derretida, e o volume de metal resultante será utilizado para a fabricação de esferas maciças com diâmetro de 1 cm, a serem usadas para confeccionar rolamentos. Para estimar a quantidade de esferas que poderão ser produzidas a partir de cada uma das peças cilíndricas, admite-se que não ocorre perda de material durante o processo de derretimento.

Quantas dessas esferas poderão ser obtidas a partir de cada peça cilíndrica?

A) 800

B) 1200

C) 2400

D) 4800

E) 6400

Ver resposta

Resposta

Alternativa D

Primeiro calcularemos o volume do cilindro de raio igual a 4.

$V=\pi r^2h$

$V=\pi\cdot4^2\cdot50$