Exercícios sobre volume do cubo
Um determinado recipiente possui formato de cubo, com arestas medindo 7 cm. Então o volume desse recipiente é de:
A) 7 cm³
B) 49 cm³
C) 196 cm³
D) 294 cm³
E) 343 cm³
A área da base de um cubo é igual a 12 cm², então o volume desse cubo, em cm³, é de:
A) 12\(\sqrt3\)
B) 18\(\sqrt2\)
C) 24\(\sqrt3\)
D) 36\(\sqrt2\)
E) 1728
Alternativa C
A área da base de um cubo é igual a²:
\(a^2=12\)
\(a=\sqrt{12}\)
\(a=\sqrt{4\cdot3}\)
\(a=2\sqrt3\)
Se a aresta mede \(2\sqrt3\):
\(V=a^3\)
\(V=\left(2\sqrt3\right)^3\)
\(V=2^3\sqrt{3^3}\)
\(V=8\sqrt{3^2\cdot3}\)
\(V=8\cdot3\sqrt3\)
\(V=24\sqrt3\)
A soma das arestas de um cubo é igual a 132 cm. Então o volume desse cubo é igual a:
A) 11 cm³
B) 121 cm ³
C) 484 cm³
D) 1331 cm³
E) 1728 cm³
Alternativa D
Para calcular o volume, antes calcularemos a medida da aresta do cubo. Como ele possui 12 arestas, dividiremos 132 por 12 para encontrar a medida de uma aresta.
132 : 12 = 11 cm
Agora, calcularemos o volume do cubo:
\(V=a^3\)
\(V={11}^3\)
\(V=1331\ cm^3\)
Um cubo será confeccionado de modo que ele tenha o mesmo volume que um paralelepípedo de dimensões 3 cm, 8 cm e 9 cm. Então a aresta desse cubo deve medir:
A) 3 cm
B) 4 cm
C) 5 cm
D) 6 cm
E) 7 cm
Alternativa D
Calculando o volume do paralelepípedo:
\(V_{paralelepípedo}=3⋅8⋅9=216\)
Sabemos que o volume do cubo é igual ao do paralelepípedo:
\(V_{cubo}=216\)
\(a^3=216\)
\(a=\sqrt[3]{216}\)
\(a=6\ \)
A aresta do cubo deve medir 6 cm.
Certo cubo possui volume igual a 13824 cm, então a soma do comprimento das arestas desse cubo é igual a:
A) 144 cm
B) 192 cm
C) 216 cm
D) 264 cm
E) 288 cm
Alternativa E
Se o volume do cubo é 13824, sabemos que:
\(a^3=13824\)
Para calcular o comprimento de uma aresta, calcularemos a raiz cúbica de 13824.
\(a=\sqrt[3]{13824}\)
\(a=24\)
Como o cubo possui 12 arestas, e cada uma mede 24 cm, então a soma do comprimento das arestas é igual a:
\(24\cdot12=288\ cm\)
No cubo a seguir foi traçada a medida da diagonal da sua face:
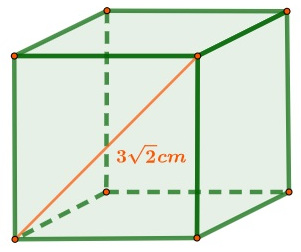
Qual é o volume do cubo?
A) 27 cm³
B) 54 cm³
C) 162 cm³
D) 210 cm³
E) 216 cm³
Alternativa A
A diagonal da face de um cubo é igual a \(a\sqrt2\):
\(a\sqrt2=3\sqrt2\)
\(a=3\)
Sabendo que a aresta mede 3 cm, calcularemos o volume do cubo:
\(V=a^3\)
\(V=3^3\)
\(V=27cm^3\)
Dois cubos, A e B, foram construídos de tal forma que a aresta do cubo B é o dobro da medida da aresta do cubo A. Quando comparamos o volume do cubo B com o volume do cubo A, podemos afirmar que:
A) o volume do cubo B é 2 vezes maior que o volume do cubo A.
B) o volume do cubo B é 4 vezes maior que o volume do cubo A.
C) o volume do cubo B é 6 vezes maior que o volume do cubo A.
D) o volume do cubo B é 8 vezes maior que o volume do cubo A.
E) o volume do cubo B é 10 vezes maior que o volume do cubo A.
Alternativa D
Se a aresta do cubo A mede a, então a aresta do cubo B medirá 2a. Calculando os seus volumes, temos que:
\(V_A=a^3\)
\(V_B=\left(2a\right)^3=8a^3\)
Note então que o volume do cubo B é 8 vezes maior que o volume do cubo A.
Um reservatório será construído no formato de um cubo. Sabendo que o seu volume deve ter mais que 512 cm³ e menos que 614 cm³, então a aresta desse cubo deve ser:
A) maior que 7,0 cm e menor que 7,5 cm.
B) maior que 7,5 cm e menor que 8,0 cm.
C) maior que 8,0 cm e menor que 8,5 cm.
D) maior que 8,5 cm e menor que 9,0 cm.
E) maior que 9,0 cm e menor que 9,5 cm.
Alternativa C
Sabemos que:
\(V=a^3\)
Assim, queremos que:
\(512<a^3<614\)
Calculando a raiz cúbica:
\(\sqrt[3]{512}<a<\sqrt[3]{614}\)
\(8<a<8,5\ \)
A aresta deve ser maior que 8,0 cm e menor que 8,5 cm.
(Fundatec 2019) Considere o cubo representado na figura a seguir:
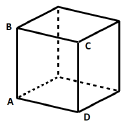
Se o perímetro do quadrado ABCD é 20, então o volume do cubo é:
A) 100
B) 125
C) 150
D) 175
E) 200
Alternativa B
O perímetro do quadrado é a soma dos seus lados. Como todos os lados são congruentes, sabemos que P = 20 e P = 4a.
Logo, temos que:
4a = 20
a = 20 : 4
a = 5
Se a aresta mede 5, então o volume do cubo é de:
\(V=a^3\)
\(V=5^3\)
\(V=125\)
(Vunesp 2015) A área de uma face de um cubo amarelo é de 104 cm² maior que a área de uma face de um cubo azul. Se a soma dos comprimentos de todas as arestas do cubo azul é igual a 132 cm, a diferença de volume, em cm³, desses dois cubos é igual a
A) 1024.
B) 1888.
C) 2044.
D) 3128.
E) 4142.
Alternativa C
Primeiramente, calcularemos o volume da aresta do cubo azul dividindo 132 por 12:
132 : 12 = 11
Como cada aresta mede 11, o volume do cubo azul é:
11³ = 1331 cm³
A área da face do cubo azul é:
11² = 121 cm²
Assim, a área da face do cubo amarelo é:
104 + 121 = 225 cm²
Se a face do cubo amarelo mede 225 cm², é possível calcular a medida da aresta desse cubo, pois temos que:
\(a^2=225\)
\(a=\sqrt{225}\)
\(a=15\ cm\)
O volume do cubo amarelo é, portanto:
15³ = 3375 cm³
Calculando a diferença entre o volume do cubo amarelo e o volume do cubo azul:
3375 – 1331 = 2044
(Enem 2014) Um fazendeiro tem um depósito para armazenar leite formado por duas partes cúbicas que se comunicam, como indicado na figura. A aresta da parte cúbica de baixo tem medida igual ao dobro da medida da aresta da parte cúbica de cima. A torneira utilizada para encher o depósito tem vazão constante e levou 8 minutos para encher metade da parte de baixo.
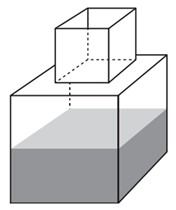
Quantos minutos essa torneira levará para encher completamente o restante do depósito?
A) 8
B) 10
C) 16
D) 18
E) 24
Alternativa B
Sendo x a medida da aresta do cubo menor, então a medida da aresta do cubo maior é 2x.
Calculando o volume do cubo maior:
\(V=\left(2x\right)^3=8x^3\)
Calculando o volume do cubo menor:
\(V=x^3\)
A metade desse volume levou 8 minutos para ser preenchida, logo a cada 8 minutos são preenchidos 4x³ de volume. Então concluímos que serão necessários 8 minutos para preencher o restante do cubo maior.
Se 8 minutos está para 4x³, dividindo por 4 descobrimos que a cada 2 minutos é preenchido x³.
Além dos 8 minutos para terminar de preencher o cubo maior, serão necessários mais 2 minutos para preencher o cubo menor, logo o tempo gasto será de 10 minutos.
(CKM Serviços 2018) Uma indústria produtora de caixas para brinquedos produz dois tipos de caixas: uma em formato de cubo e outra em formato de paralelepípedo reto retângulo. O cubo é formado por quadrados cujas arestas medem 30 cm cada uma, e o paralelepípedo tem como dimensões 20 cm de comprimento, 20 cm de altura e 10 cm de largura. Entre as duas caixas, qual delas comporta maior volume e qual é o valor desse volume?
A) O cubo, que comporta um volume de 27.000 cm³.
B) O paralelepípedo, que comporta um volume de 40.000 cm³.
C) O cubo, que comporta um volume de 270 cm³.
D) O paralelepípedo, que comporta um volume de 4.000 cm³.
E) O cubo, que comporta um volume de 2.700 cm³.
Alternativa A
Primeiramente, calcularemos o volume de cada uma das caixas. Começando pela caixa que tem formato de um cubo:
\(V_{cubo}=a^3\)
\(V_{cubo}={30}^3\)
\(V_{cubo}=27000\ cm^3\)
Agora, da caixa que possui formato de paralelepípedo:
\(V_{paralelepípedo}=a⋅b⋅c\)
\(V_{paralelepípedo}=20⋅20⋅10\)
\(V_{paralelepípedo}=4000\ cm^3\)
Portanto, o cubo é o que possui o maior volume, pois ele comporta 27000 cm³.
