Exercícios sobre volume dos sólidos geométricos
Um prisma tem base formada por um triângulo retângulo com catetos medindo 24 cm e 18 cm. Sabendo que a altura desse prisma é de 20 cm, então o seu volume é igual a:
A) 4320 cm³
B) 3440 cm³
C) 2880 cm³
D) 2560 cm³
E) 2160 cm³
Alternativa A
O volume de um prisma é igual ao produto da área da base pela altura. Sabendo que a base é um triângulo retângulo, a sua área é igual ao produto entre os catetos divido por 2.
\(A_b=\frac{24\cdot18}{2}\)
\(A_b=216\ cm^2\)
Agora calculando o volume, temos que:
\(V=A_b\cdot h\)
\(V=216\ \cdot20\ \)
\(V=4320\ cm^3\)
Um reservatório de gás possui formato de cilindro, com 2 metros de diâmetro e 2 metros de altura. Utilizando π = 3,1, o volume desse reservatório é de:
A) 1,5 cm³
B) 1,6 cm³
C) 3,1 cm³
D) 6,2 cm³
E) 12,4 cm³
Alternativa D
O volume do cilindro é calculado pela fórmula \(V=\pi r^2\cdot h\).
Dados:
-
\( \pi=3,1\)
-
\(h=2\)
Sabendo que o diâmetro é igual a 2 metros, então o raio é a metade do diâmetro:
\(r=1\)
Calculando o volume:
\(V=3,1\cdot1^2\cdot2\)
\(V=3,1\cdot1\cdot2\)
\(V=6,2\ cm^3\)
Buscando inovar nas embalagens, uma empresa de cosméticos decidiu fazer o lançamento de um perfume com o nome Egito, e a embalagem desse perfume tem formato de uma pirâmide de base quadrada. Sabendo que essa embalagem tem base formada por um quadrado com lados medindo 6 centímetros e tem 10 centímetros de altura, então o seu volume é de:
A) 360 cm³
B) 240 cm³
C) 210 cm³
D) 150 cm³
E) 120 cm³
Alternativa E
Calculando o volume da pirâmide, ele é dado pela fórmula:
\(V=\frac{A_b\cdot h}{3}\)
Como a base da pirâmide é um quadrado:
\(A_b=l^2\)
\(A_b=6²\)
\(A_b=36\)
Calculando o volume:
\(V=\frac{36\cdot10}{3}\)
\(V=\frac{360}{3}\)
\(V=120\ cm^3\)
Uma empresa decidiu criar um recipiente esférico que tem volume igual a 2916 cm³. Utilizando π = 3, o raio desse recipiente deve ser igual a:
A) 6 cm
B) 7 cm
C) 8 cm
D) 9 cm
E) 10 cm
Alternativa D
Para calcular o volume da esfera, utilizamos a fórmula:
\(V=\frac{4\pi r^3}{3}\)
Sabendo que V=2916 e utilizando 3 como aproximação para o valor de π , temos que:
\(2916=\frac{4\cdot3\cdot r^3}{3}\)
\(2916=4r^3\)
\(4r^3=2916\)
\(r^3=\frac{2916}{4}\)
\(r^3=729\)
\(r=\sqrt[3]{729}\)
\(r=9 \) cm
Em uma caçamba, são empilhadas 25 caixas no formato de cubo. Sabendo que cada caixa tem 0,8 metros de aresta, então o volume ocupado pelas 25 caixas é igual a:
A) 15,8 m³
B) 14,0 m³
C) 13,4 m³
D) 12,8 m³
E) 10,5 m³
Alternativa D
Calculando o volume de um cubo:
\(V={0,8}^3\)
\(V=0,512\ m³\)
Como são 25 cubos, multiplicaremos o volume de um cubo por 25:
\(25V=25\cdot0,512\) = \(12,8\ m³\)
(Fauel) O cone circular é considerado reto quando a projeção ortogonal do vértice sobre o plano da base é o ponto central da base. A altura de um cone circular reto mede o dobro da medida do raio da base e o comprimento da circunferência dessa base é 20π cm, então o volume desse cone é: (adote π = 3)
A) 2000 cm³
B) 3000 cm³
C) 5000 cm³
D) 6000 cm³
Alternativa D
Para encontrar o raio da base, utilizaremos comprimento igual a \(20\pi\):
C = \(2\pi\cdot r\)
\(20\pi=2\ \pi r\)
\(\frac{20\pi}{2\pi}=r\)
\(r=10\ \)
Sabendo que o raio mede 10, e que a altura é o dobro do raio, então \(h=20\).
Calculando o volume do cilindro e utilizando \(\pi=3\):
\(V=\pi r^2\cdot h\)
\(V=3\cdot{10}^2\cdot20\)
\(V=3\cdot100\cdot20\ \)
\(V=6000\ cm³\)
Um reservatório será construído no formato de um cilindro com raio de 5 metros e volume de 785 m³. Utilizando π = 3,1, a altura desse reservatório deverá ser de:
A) 8 m
B) 9 m
C) 10 m
D) 11 m
E) 12
Alternativa B
O volume de um cilindro é calculado por:
\(V=\pi r^2\cdot h\)
Substituindo pelos dados da questão, temos que:
-
r = 5
-
V = 620
-
π = 3,1
\(697,5=3,1\cdot5^2\cdot h\)
\(697,5=77,5\ h\)
\(\frac{6975}{77,5}=h\)
\(h=9\)
Uma piscina tem o formato de um paralelepípedo retângulo com 1,5 metros de profundidade, 3 metros de largura e 6 metros de comprimento. Sabendo que 3/4 dessa piscina estão cheios, então a quantidade de água que falta em litros para preencher toda a piscina é de:
A) 27.000
B) 20.250
C) 13.500
D) 6750
E) 5250
Alternativa D
Calculando o volume, temos que:
\(V=1,5\cdot3\cdot6=27\ m^3\)
Transformando para litros, multiplicaremos por 1000:
\(27\cdot1000=27.000\ l\)
Se o volume total é 27.000 litros, e 3/4 estão cheios, então 1/4 está vazio.
\(27.000\cdot\frac{1}{4}=6750\)
(Enem 2021) Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
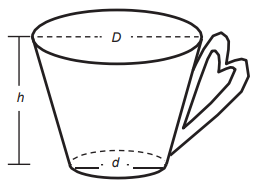
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base). Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
A) 216
B) 408
C) 732
D) 2196
E) 928
Alternativa C
Calculando o volume do tronco de cone, temos que:
\(V=\frac{\pi h}{3}\cdot\left(R^2+R\cdot r+r^2\right)\)
\(V=\frac{3\cdot12}{3}\cdot\left(5^2+5\cdot4+4^2\right)\)
\(V=12\cdot\left(25+20+16\right)\)
\(V=12\cdot61\)
\(V=732\ cm^3\)
(Fundatec) Um enfeite em formato de pirâmide regular e de base quadrada tem o lado da base medindo 10 cm e a altura de 30 cm. Qual é o volume em cm³ dessa pirâmide?
A) 300
B) 690
C) 830
D) 950
E) 1000
Alternativa E
Calculando o volume, temos que:
\(V=\frac{A_b\cdot h}{3}\)
Como a base é um quadrado:
\(A_b=l^2={10}^2=100\)
Então, calculando o volume:
\(V=\frac{100\cdot30}{3}=100\cdot10=1000\ cm^3\)
Analise o cone a seguir:
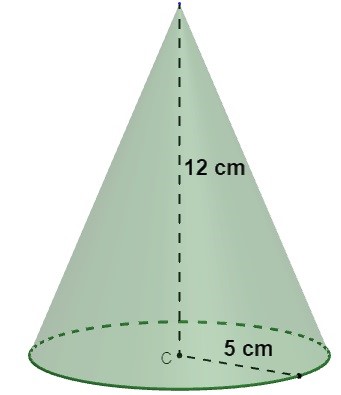
Utilizando π = 3, o volume do cone é igual a:
A) 375 cm³
B) 250 cm³
C) 125 cm³
D) 75 cm³
E) 30 cm³
Alternativa C
Dados:
-
r = 5
-
h = 12
-
π = 3
Calculando o volume do cone, temos que:
\(V=\frac{\pi r^3}{3}\)
\(V=\frac{3\cdot5^3}{3}\)
\(V=5^3\)
\(V=125\ cm³\)
Um prisma de base retangular possui as medidas retratadas a seguir.
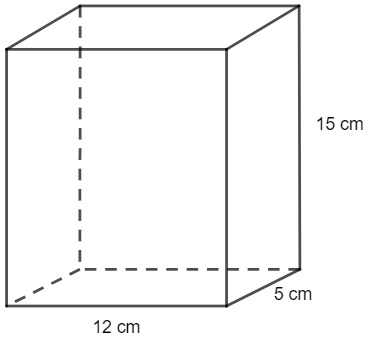
Analisando a imagem, o volume do prisma é igual a:
A) 300 cm³
B) 500 cm³
C) 600 cm³
D) 900 cm³
E) 1200 cm³
Alternativa D
Calculando o volume do prisma, temos que:
\(V=12\cdot5\cdot15\)
\(V=60\cdot15\)
\(V=900\ cm^3\)
