Home
Exercícios de Matemática
Exercícios sobre volume do prisma

Exercícios sobre volume do prisma

Resolva esta lista de exercícios sobre volume do prisma, calculado quando multiplicamos a área da base pela sua altura. Publicado por: Raul Rodrigues de Oliveira

Imprimir

Questão 1

O volume de um prisma é dado pela fórmula:

A) Área da base + altura

B) Área da base × altura

C) Perímetro × altura

D) Área da lateral + altura

E) Área da base ÷ altura

Ver resposta

Resposta

Alternativa B.

O volume do prisma é calculado multiplicando a área da sua base pela altura.

Questão 2

Um prisma tem base quadrada de lado 3 cm e altura 5 cm. Qual seu volume?

A) 30 cm³

B) 45 cm³

C) 50 cm³

D) 60 cm³

E) 90 cm³

Ver resposta

Resposta

Alternativa B.

Se a área do prisma é quadrada, então a área da base será igual ao quadrado de 3, ou seja:

A_b= 3² = 9

Agora basta multiplicar pela altura:

V = A_b ⋅ h

V = 9 ⋅ 5

V = 45 cm³

Questão 3

Um prisma triangular tem área da base 12 cm² e altura 4 cm, então o seu volume:

A) 24 cm³

B) 48 cm³

C) 36 cm³

D) 60 cm³

E) 30 cm³

Ver resposta

Resposta

Alternativa B.

Se a área da base é 12 cm² e a altura é 4 cm, então temos que:

V = A_b ⋅ h

V = 12 ⋅ 4

V = 48 cm³

Questão 4

Um prisma triangular tem área da base 24 cm² e seu volume é de 288 cm³, então qual é a altura desse prisma?

A) 10 cm

B) 12 cm

C) 15 cm

D) 18 cm

E) 20 cm

Ver resposta

Resposta

Alternativa B.

Sabendo que o volume do prisma é o produto da área da base pela altura, temos que:

$V=A_b \cdot h$

$288 = 24 h$

$\frac{288}{24} = h$

$12 = h$

$h=12 cm$

Questão 5

Heitor construiu uma caixa de madeira no formato de um paralelepípedo (prisma retangular) para guardar ferramentas. As dimensões internas da caixa são: 80 cm de comprimento, 40 cm de largura e 25 cm de altura. Qual o volume da caixa?

A) 8000 cm³

B) 20.000 cm³

C) 60.000 cm³

D) 80.000 cm³

E) 100.000 cm³

Ver resposta

Resposta

Alternativa D.

Como o prisma é um paralelepípedo, para calcular seu volume, basta multiplicar as suas 3 dimensões, logo, temos que:

V = 80 ⋅ 40 ⋅ 25

V = 80.000 cm³

Questão 6

Um tanque em forma de prisma de base triangular tem 3 metros de base e 4 metros de altura na base. A altura do prisma é 10 metros. Qual o volume de água que ele comporta?

A) 50 m³

B) 60 m³

C) 70 m³

D) 40 m³

E) 100 m³

Ver resposta

Resposta

Alternativa B.

Primeiro calcularemos a área da base:

$A_b = \frac{3 \ \cdot \ 4}{2}$

$A_b=3 \cdot 2$

$A_b=6\ cm^2$

Sabendo que a área da base é de 6 centímetros, então, para calcular o volume, temos que:

$V=A_b \cdot h$

$V= 6 \cdot 10$

$V=60 \ m^3$

Questão 7

(Enem) Um artesão possui potes cilíndricos de tinta cujas medidas externas são 4 cm de diâmetro e 6 cm de altura. Ele pretende adquirir caixas organizadoras para armazenar seus potes de tinta, empilhados verticalmente com tampas voltadas para cima, de forma que as caixas possam ser fechadas. No mercado, existem cinco opções de caixas organizadoras, com tampa, em formato de paralelepípedo reto-retângulo, vendidas pelo mesmo preço, possuindo as seguintes dimensões internas:

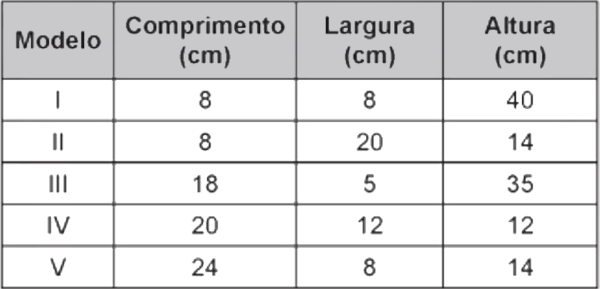
Tabela com informações sobre 5 modelos de caixas organizadoras em exercício do Enem sobre volume do prisma.

Qual desses modelos o artesão deve adquirir para conseguir armazenar o maior número de potes por caixa?

A) I.

B) II.

C) III.

D) IV.

E) V.

Ver resposta

Resposta

Alternativa D.

Analisaremos a capacidade de cada um dos modelos:

Modelo I:

Comprimento 8 cm:

8 : 4 = 2 latas

Largura 8 cm:

8 : 4 = 2 latas

Altura 40 cm:

40 : 6 = 6,66… = 6 latas

Capacidade:

2 ⸳ 2 ⸳ 6 = 24 latas

Modelo II:

Comprimento 8 cm:

8 : 4 = 2 latas

Largura 20 cm:

20 : 4 = 5 latas

Altura 14 cm:

14 : 6 = 2,333… = 2 latas

Capacidade:

2 ⸳ 5 ⸳ 2 = 20 latas

Modelo III:

Comprimento 18 cm:

18 : 4 = 4,5 = 4 latas

Largura 5 cm:

5 : 4 = 1,25 = 1 lata

Altura 35 cm :

35 : 6 = 5,8 = 5 latas

Capacidade:

4 ⸳ 1 ⸳ 5 = 20 latas

Modelo IV:

Comprimento 20 cm:

20 : 4 = 5 latas

Largura 12 cm:

12 : 4 = 3 latas

Altura 12 cm:

12 : 6 = 2 latas

Capacidade:

5 ⸳ 3 ⸳ 2 = 30 latas

Modelo V:

Comprimento 24 cm:

24 : 4 = 6 latas

Largura 8 cm:

8 : 4 = 2 latas

Altura 14 cm:

14 : 6 = 2,333… = 2 latas

Capacidade:

6 ⸳ 2 ⸳ 2 = 24 latas

A caixa organizadora que tem maior capacidade para as latas é o modelo IV.

Questão 8

(Enem) Uma pessoa comprou um aquário em forma de um paralelepípedo retângulo reto, com 40 cm de comprimento, 15 cm de largura e 20 cm de altura. Chegando em casa, colocou no aquário uma quantidade de água igual à metade de sua capacidade. A seguir, para enfeitá-lo, irá colocar pedrinhas coloridas, de volume igual a 50 cm³ cada, que ficarão totalmente submersas no aquário.

Após a colocação das pedrinhas, o nível da água deverá ficar a 6 cm do topo do aquário.

O número de pedrinhas a serem colocadas deve ser igual a

A) 48.

B) 72.

C) 84.

D) 120.

E) 168.

Ver resposta

Resposta

Alternativa A.

Para encontrar calcular o volume, é importante ressaltar que o volume da pedrinha será igual ao volume que aumentou no líquido do aquário.

A metade da capacidade do aquário tem água e pedrinhas, e sabemos que a metade de 20 é 10.

Calculando que 10 – 6 = 4 cm, então a altura da água aumentou 4 cm quando foram acrescentadas as pedrinhas.

Logo, para calcular o volume, temos que:

V = 40 ⸳ 15 ⸳ 4 = 2400 cm³

Cada pedrinha tem 50 cm³ de volume:

2400 : 50 = 48 pedrinhas

Questão 9

(Enem) Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.

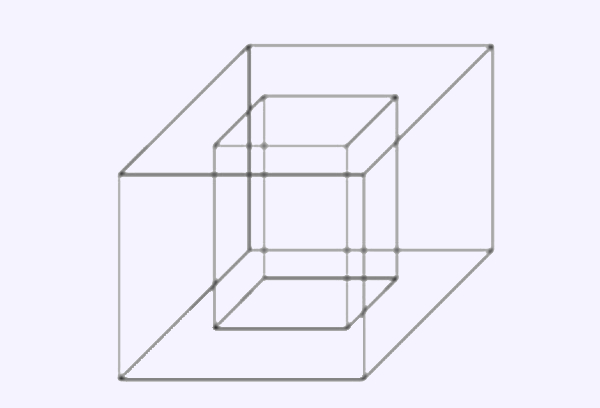
Ilustração de um porta-lápis de madeira construído no formato cúbico em exercício do Enem sobre volume do prisma.

O volume de madeira utilizado na confecção desse objeto foi de

A) 12 cm³

B) 64 cm³

C) 96 cm³

D) 1216 cm³

E) 1728 cm³

Ver resposta

Resposta

Alternativa D.

O cubo é um prisma de base quadrada de arestas com mesmas medidas, logo, para calcular o volume dele, temos que:

$V=a \cdot a \cdot a=a^3$

Então, para calcular o volume de madeira, calcularemos o volume do maior cubo menos o menor cubo, logo, temos que:

$V=12^3-8^3$

$V=1728 - 512$

$V=1216 \ cm^3$

Questão 10

(Enem) Uma lata de tinta, com a forma de um paralelepípedo retangular reto, tem as dimensões, em centímetros, mostradas na figura.

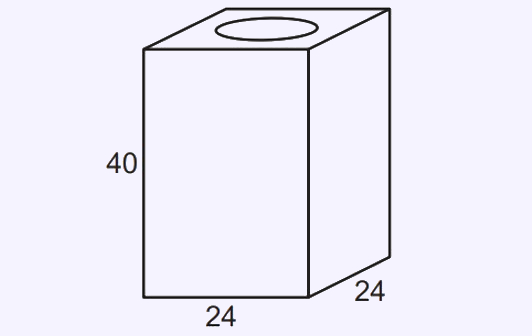
Ilustração de uma lata de tinta em exercício do Enem sobre volume do prisma.

Será produzida uma nova lata, com os mesmos formato e volume, de tal modo que as dimensões de sua base sejam 25% maiores que as da lata atual.

Para obter a altura da nova lata, a altura da lata atual deve ser reduzida em:

A) 14,4%

B) 20,0%

C) 32,0%

D) 36,0%

E) 64,0%

Ver resposta

Resposta

Alternativa D.

Seja x a taxa de redução de altura da lata, sabendo que houve um aumento de 25% nas dimensões, temos:

$24 \cdot 24 \cdot 40 = (1{,}25 \cdot 40) \cdot (1{,}25 \cdot 40) \cdot (1 - x) \cdot 40$

$24 \cdot 24 \cdot 40 = 1{,}25^2 \cdot (1 - x) \cdot 24 \cdot 24 \cdot 40$

$\frac{24 \ \cdot \ 24 \ \cdot \ 24}{24 \ \cdot \ 24 \ \cdot \ 40} = 1{,}25^2 \cdot (1 - x)$

$1 = 1,25^2 \cdot (1-x)$

$1 = \left( \frac{5}{4} \right)^2 \cdot (1 - x)$

$1 = \frac{25}{16} \cdot (1 - x)$

$1 \cdot 16 = 25 \cdot (1 - x)$

$16 = 25 - 25x$

$16 - 25 = -25x$

$-9 = - 25x$

$25x=9$

$x = \frac{9}{25}$

$x=0,36$

Questão 11

Uma empresa de materiais recicláveis empilha blocos prismáticos com base hexagonal regular. Cada base tem área de 25 m², e cada bloco tem altura de 2,5m. Qual o volume de um bloco?

A) 50 m³

B) 62,5 m³

C) 55 m³

D) 45 m³

E) 52,5 m³

Ver resposta

Resposta

Alternativa B.

A área da base mede 25 m² e a altura é 2,5, então temos que:

V = 25 ⋅ 2,5

V = 62,5 m³

Questão 12