Exercícios sobre lei da velocidade para reações não elementares
Uma certa reação química genérica, representada pela equação abaixo:
A + 4 B → X + Y
É formada após a ocorrência de três etapas, as quais estão representadas a seguir:
Reação I: A + 2 B → C + D (etapa lenta)
Reação II: C + B → X
Reação III: D + B → Y (etapa rápida)
Qual das alternativas abaixo contém a expressão da velocidade para essa reação genérica?
a) v = k.[A]2.[B]1
b) v = k.[A]1.[B]2
c) v = k.[A]1.[B]1
d) v = k.[B]2
Letra b). O exercício pede para determinarmos a expressão da velocidade da reação não elementar abaixo:
A + 4 B → X + Y
Como a velocidade de uma reação é determinada pela sua etapa lenta, para montar a expressão da velocidade, devemos utilizar:
A + 2 B → C + D (etapa lenta)
Nessa etapa, temos apenas o reagente A, e o seu coeficiente estequiométrico na equação é igual a 1. Assim, a expressão da velocidade será:
v = k.[A]1.[B]2
Quando o dióxido de nitrogênio é colocado para reagir com o gás flúor, o composto fluoreto de nitrila é originado, segundo a equação abaixo:
2 NO2(g) + F2(g) → 2 NO2F(g)
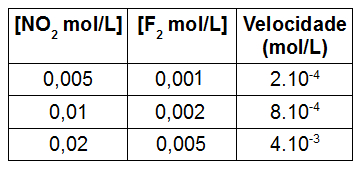
Foram realizados alguns estudos cinéticos com essa reação, nos quais foram alteradas as concentrações molares dos reagentes, resultando em determinados valores de velocidade, como podemos observar na tabela a seguir:
Qual das alternativas abaixo contém a ordem da reação e a sua expressão da velocidade?
a) Ordem 1, v = k[NO2]1
b) Ordem 2, v = k[NO2]1[F2]1
c) Ordem 3, v = k[NO2]2[F2]1
d) Ordem 1, v = k[F2]1
Letra b). Para montar a expressão da velocidade presente na alternativa b, não é possível determinar a ordem de cada um dos reagentes de forma individual porque os valores das concentrações variam de um experimento para outro. Assim, é necessário analisar os experimentos aos pares:
1º Passo: Entre os experimentos 1 e 2:
- Concentração de NO2: dobra de valor, pois passa de 0,01 para 0,02;
- Concentração de F2: quintuplica de valor, pois passa de 0,002 para 0,01;
- Velocidade: quadruplica de valor, pois passa de 8.10-4 para 4.10-3.
Assim, a análise deve ser:
2.[NO2].2[F2]= 4.v
4.[NO2].[F2]= 4.v
Como os valores apresentam a mesma base, logo os reagentes apresentam ordem 1.
2º Passo: Analisando outros experimentos, o resultado será o mesmo. Entre os experimentos 2 e 3:
- Concentração de NO2: dobra de valor, pois passa de 0,005 para 0,01;
- Concentração de F2: o valor aumenta duas vezes e meia, pois passa de 0,002 para 0,005;
- Velocidade: quintuplica de valor, pois passa de 8.10-4 para 4.10-3.
Assim, a análise deve ser:
2.[NO2].2,5[F2]= 5.v
5.[NO2].[F2]= 5.v
Reforça-se o fato de que o que ocorre na concentração dos reagentes, ocorre com a velocidade, proporcionalmente. Portanto, ambos são de ordem 1.
3º Passo: Determinar a ordem da reação.
Para determinar a ordem da reação, basta somar a ordem do reagente NO2 com a ordem do reagente F2, o que resulta em 2.
4º Passo: Montar a expressão da velocidade.
Para montar a expressão da velocidade, basta multiplicar as concentrações dos reagentes, elevadas às suas respectivas ordens, pela constante (k):
v = k[NO2]1[F2]1
(UEMG) Uma reação química hipotética é representada pela seguinte equação:
A(g) + B(g) → C(g) + D(g)
e ocorre em duas etapas:
A(g) → E(g) + D(g) (Etapa lenta)
E(g) + B(g ) → C(g) (Etapa rápida)
A lei da velocidade da reação pode ser dada por
a) v = k.[A]1
b) v = k.[A]1.[B]1
c) v = k.[C]1.[D]1
d) v = k.[E]1.[B]1
Letra a). O exercício pede para determinar a expressão da velocidade da reação não elementar abaixo:
A(g) + B(g) → C(g) + D(g)
Como a velocidade de uma reação é determinada pela sua etapa lenta, para montar sua expressão da velocidade, deve-se utilizar a expressão dessa etapa:
A(g) → E(g) + D(g) (Etapa lenta)
Nessa etapa, temos apenas o reagente A, e o seu coeficiente estequiométrico na equação é igual a 1. Dessa forma, a expressão da velocidade será:
v = k.[A]1
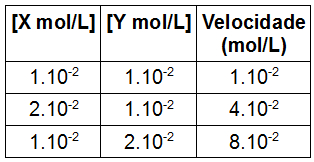
(UERN) No estudo cinético da reação representada por: X + Y → Z, foram encontradas as seguintes variações de concentração e velocidade em um intervalo de tempo:
Analisando os resultados, a expressão correta da Lei da Velocidade para essa reação é:
a) v = k.[x]2.[y]2
b) v = k.[x]3. [y]3
c) v = k.[x]3.[y] 2
d) v = k.[x]2.[y]3
Letra d). Para montar a expressão da velocidade presente na alternativa d, devemos realizar os seguintes passos:
1º Passo: Determinar a ordem do reagente X.
Para isso, devemos escolher duas etapas em que a concentração de X sofre alteração, e que a de Y não sofra alteração. Portanto, as etapas escolhidas são a 1a e a 2a, nas quais temos as seguintes mudanças:
- Concentração de X: dobra de valor, pois passa de 1.10-2 para 2.10-2;
- Velocidade: quadruplica de valor, pois passa de 1.10-2 para 4.10-2.
Assim, a análise deve ser:
2.[X] = 4.v
Colocando os dois valores na mesma base:
2.[X] = 22.v
Temos que a diferença é o expoente 2 e, por isso, a ordem de X será igual a 2.
2º Passo: Determinar a ordem do reagente Y.
Para tal, devemos escolher duas etapas em que a concentração de Y sofre alteração, e que a de X não sofra alteração. As etapas escolhidas são, portanto, a 1a e a 3a, nas quais temos as seguintes mudanças:
-
Concentração de Y: dobra de valor, pois passa de 1.10-2 para 2.10-2;
-
Velocidade: octuplica de valor, pois passa de 1.10-2 para 8.10-2.
Assim, a análise deve ser:
2.[X] = 8.v
Colocando os dois valores na mesma base:
2.[X] = 23.v
Temos que a diferença é o expoente 2 e, assim, a ordem de X será igual a 3.
3º Passo: Montar a expressão da velocidade.
Para montar a expressão da velocidade, basta multiplicar as concentrações dos reagentes, elevadas às suas respectivas ordens, pela constante (k):
v = k.[x]2.[y]3
