Exercícios sobre moléculas inorgânicas apolares
Dentre as substâncias representadas abaixo, assinale a que é constituída por moléculas polares:
a) CO2
b) H2O
c) BF3
d) Cl2
e) CCl4
Letra b) Para determinarmos se uma molécula é apolar ou polar, devemos antes de mais nada conhecer sua geometria e todos os vetores momento dipolar existentes.
a) molécula de geometria linear, que apresenta dois vetores, de sentidos contrários, na direção de cada oxigênio. Automaticamente esses vetores se anulam, levando o vetor momento dipolar resultante da molécula a ser igual a 0. Logo, a molécula é apolar.
b) molécula de geometria angular, apresentando dois vetores diagonais no sentido do oxigênio. Aqui, como dois deles são diagonais, é utilizada a regra do paralelogramo, com a qual surge um único vetor momento dipolar. Assim, a molécula apresenta um vetor momento dipolar resultante diferente de 0. Logo, ela é polar.
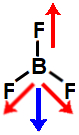
c) molécula de geometria trigonal, apresentando três vetores no sentido de cada átomo de flúor. Aqui, como dois deles são diagonais, é utilizada a regra do paralelogramo, com a qual surge um único vetor momento dipolar. Como os dois vetores finais estão em sentidos diferentes, o vetor momento dipolar resultante da molécula é igual a 0. Logo, ela é apolar.
d) molécula linear, formada por dois átomos iguais, ou seja, de mesma eletronegatividade. Logo, trata-se de uma molécula apolar.
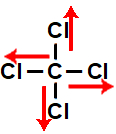
e) molécula tetraédrica, que apresenta quatro vetores, sendo dois na horizontal, em sentidos opostos, e outros dois na vertical, também em sentidos opostos. Assim, o vetor momento dipolar resultante da molécula é igual a 0. Logo, a molécula é apolar.
Com base nas fórmulas moleculares dos compostos e no conhecimento da diferença de eletronegatividade de cada elemento na Tabela Periódica, assinale a opção que apresenta o composto cujo momento dipolar é zero, ou seja, é apolar.
a) H2O
b) NH3
c) BeH2
d) CO
e) HF
Letra c) Para determinarmos se uma molécula é apolar ou polar, devemos antes de mais nada conhecer sua geometria e todos os vetores momento dipolar existentes:
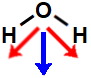
a) molécula de geometria angular, apresentando dois vetores diagonais no sentido do oxigênio. Aqui, como dois deles são diagonais, é utilizada a regra do paralelogramo, com a qual surge um único vetor momento dipolar. Assim, a molécula apresenta um vetor momento dipolar resultante diferente de 0. Logo, ela é polar.
.jpg)
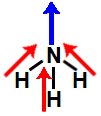
b) molécula de geometria piramidal, apresentando três vetores no sentido do átomo de nitrogênio. Aqui, como dois deles são diagonais, é utilizada a regra do paralelogramo, com a qual surge um único vetor momento dipolar. Como os dois vetores finais estão no mesmo sentido, o vetor momento dipolar resultante da molécula é diferente de 0. Logo, ela é polar.
c) molécula de geometria linear, que apresenta dois vetores, de sentidos contrários, na direção de cada hidrogênio. Automaticamente, esses vetores se anulam, levando o vetor momento dipolar resultante da molécula a ser igual a 0. Logo, a molécula é apolar.
d) molécula linear, formada por dois átomos diferentes, ou seja, de diferente eletronegatividade. Logo, trata-se de uma molécula polar.
e) molécula linear, formada por dois átomos diferentes, ou seja, de diferente eletronegatividade. Logo, trata-se de uma molécula polar.
(UFRGS-RS) As substâncias SO2 e CO2 apresentam moléculas que possuem ligações polarizadas. Sobre as moléculas dessas substâncias é correto afirmar que:
a) ambas são polares, pois apresentam ligações polarizadas.
b) ambas são apolares, pois apresentam geometria linear.
c) apenas o CO2 é apolar, pois apresenta geometria linear.
d) ambas são polares, pois apresentam geometria angular.
e) apenas o SO2 é apolar, pois apresenta geometria linear.
Letra c) Para determinarmos se uma molécula é apolar ou polar, devemos antes de mais nada conhecer sua geometria e todos os vetores momento dipolar existentes:
-
CO2- molécula de geometria linear, que apresenta dois vetores, de sentidos contrários, na direção de cada oxigênio. Automaticamente, esses vetores se anulam, levando o vetor momento dipolar resultante da molécula a ser igual a 0. Logo, a molécula é apolar.
.jpg){kind=small}
-
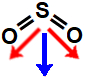
SO2- molécula de geometria angular, apresentando dois vetores diagonais no sentido dos oxigênios. Aqui, como dois deles são diagonais, é utilizada a regra do paralelogramo, com a qual surge um único vetor momento dipolar. Assim, a molécula apresenta um vetor momento dipolar resultante diferente de 0. Logo, ela é polar.
(UFRS) O momento dipolar é a medida quantitativa da polaridade de uma ligação. Em moléculas apolares, a resultante dos momentos dipolares referentes a todas as ligações apresenta valor igual a zero. Entre as substâncias covalentes abaixo:
I) CH4
II) CS2
III) HBr
IV) N2
Quais são as que apresentam a resultante do momento dipolar igual a zero?
a) Apenas I e II.
b) Apenas II e III.
c) Apenas I, II e III.
d) Apenas I, II e IV.
e) I, II, III e IV.
Letra d) Para determinarmos se uma molécula é apolar, ou seja, que apresenta vetor momento dipolar resultante igual a 0, devemos antes de mais nada conhecer sua geometria e todos os vetores momento dipolar existentes:
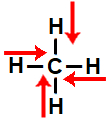
I - molécula tetraédrica, que apresenta quatro vetores, sendo dois na horizontal, em sentidos iguais e direções diferentes, e dois na vertical, em sentidos iguais e direções opostas. Assim, o vetor momento dipolar resultante da molécula é igual a 0. Logo, a molécula é apolar.
II - molécula de geometria linear, que apresenta dois vetores, de sentidos contrários, na direção de cada oxigênio. Automaticamente, esses vetores se anulam, e o vetor momento dipolar resultante da molécula é igual a 0. Logo, a molécula é apolar.
III - molécula linear, formada por dois átomos diferentes, ou seja, de diferente eletronegatividade. Logo, trata-se de uma molécula polar.
.jpg){kind=small}
d - molécula linear, formada por dois átomos iguais, ou seja, de mesma eletronegatividade. Logo, trata-se de uma molécula apolar.
