Exercícios sobre nível de intensidade sonora

(Cesgranrio) Quando a orelha humana é submetida continuamente a ruídos de nível sonoro superior a 85 dB, sofre lesões irreversíveis. Por isso, o Ministério do Trabalho estabelece o tempo máximo diário que um trabalhador pode ficar exposto a sons muito intensos. Esses dados são apresentados a seguir:

Nível sonoro (dB); 85; tempo máximo de exposição (h); 8

Nível sonoro (dB); 90; tempo máximo de exposição (h); 4

Nível sonoro (dB); 95; tempo máximo de exposição (h); 2

Nível sonoro (dB); 100; tempo máximo de exposição (h); 1

Observa-se, portanto, que a cada aumento de 5 dB no nível sonoro, o tempo máximo de exposição cai para a metade. Sabe-se ainda que, ao assistir a um Show de Rock, espectadores próximos às caixas de som estão expostos a um nível sonoro de 110 dB. O nível de intensidade sonora (N) é expresso em decibels (dB) por:

N = 10. log  I 
                  I₀

I = intensidade sonora fornecida pela caixa de som; I₀ = intensidade padrão, corresponde ao limiar da audição (para o qual N = 0). Para o nível de intensidade N = 120 dB, a intensidade sonora, fornecida pela caixa de som, deverá ser de:

a)10¹⁴ I₀

b) 10¹²I₀

c) 1200 I₀

d) 120 I₀

e) 12I₀

Um estudante, após assistir a uma aula de Física sobre intensidade sonora, resolveu descobrir qual era o nível sonoro marcado na sala de sua casa quando o horário de tráfego de veículos na região onde mora era intenso. Um aplicativo de celular que simula um decibelímetro revelou que o nível sonoro era de 90 dB. Sabendo que a intensidade mínima que corresponde ao limiar da audição humana corresponde a 10 ^{– 12} W/m², determine, em W/m², a intensidade sonora referente à medida feita pelo garoto:

a) 10 ^{– 9}

b) 10 ^{– 6}

c) 10 ^{– 5}

d) 10 ^{– 3}

e) 10 ^{– 2}

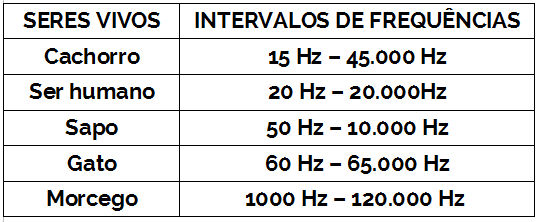
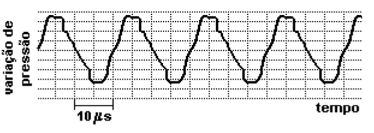
(FUVEST) O som de um apito é analisado com o uso de um medidor que, em sua tela, visualiza o padrão apresentado na figura a seguir. O gráfico representa a variação da pressão que a onda sonora exerce sobre o medidor, em função do tempo, em μs (1μs = 1 x10 ^{– 6} s). Analisando a tabela de intervalos de frequências audíveis, por diferentes seres vivos, conclui-se que esse apito pode ser ouvido apenas por:

a) seres humanos e cachorros

b) seres humanos e sapos

c) sapos, gatos e morcegos

d) gatos e morcegos

e) morcego

Durante um jogo de futebol, a intensidade sonora é próxima de 80 dB. Supondo que, no momento do gol, a intensidade sonora torne-se 1000 vezes maior, qual é o valor do nível sonoro, em dB, no momento do gol?

a) 85 dB

b) 185 dB

c) 110 dB

d) 100 dB

e) 90 dB

Durante um show, a intensidade sonora nas proximidades do palco era de aproximadamente 1W/m². Sabendo que a intensidade mínima para a audição humana é de 10 ^{– 12} W/m², determine o nível de intensidade sonora na região do palco:

a) 80 dB

b) 130 dB

c) 110 dB

d) 120 dB

e) 90 dB