Exercícios sobre cálculo de raízes não exatas
Qual a medida da diagonal de um quadrado cuja área mede 450 cm2?
a) 30 cm
b) 15·√2 cm
c) √2 cm
d) 15 cm
e) 45 cm
Lembre-se de que a área do quadrado é obtida a partir da seguinte fórmula:
A = l2
Para resolver esse problema, substitua o 450 cm2 em A:
A = l2
450 = l2
l2 = 450
√l2 = √450
É necessário fazer a decomposição em fatores primos de 450 para obter: 450 = 2·32·52. Assim, temos que:
l = √(2·32·52)
l = 3·5·√2
l = 15·√2
A diagonal do quadrado pode ser encontrada da seguinte maneira:
d = l·√2
d = 15·√2·√2
d = 15·(√2)2
d = 15·2
d = 30 cm
Gabarito: letra A.
Em determinada época do ano, a sombra projetada no chão, em um horário próximo ao pôr do sol, é exatamente o quadrado da altura do objeto que projeta essa sombra. Sabendo que o comprimento da sombra de um prédio é de 1728 metros, qual das opções a seguir mais se aproxima de sua altura?
a) 60 metros
b) 50 metros
c) 40 metros
d) 30 metros
e) 20 metros
Para resolver esse problema, basta calcular a raiz quadrada de 1728. Para tanto, observe a decomposição de 1728 em fatores primos:
1728 = 2·2·3·3·3·4·4
A raiz quadrada de 1728 é:
√1728 = √(2·2·3·3·3·4·4) = √(22·32·3·42) = 2·3·4√3 = 24√3
Como a raiz de três não é exata, é necessário fazer uma aproximação. Sabendo que √1 = 1 e que √4 = 2, então, √3 está entre 1 e 2. A melhor aproximação com uma casa decimal é 1,7. Então, para finalizar, basta multiplicar 24 por 1,7.
24√3 = 24·1,7 = 40,8 metros, aproximadamente.
Gabarito: letra C.
Uma cerca é composta de três paredes, duas iguais que medem √48 m e uma que mede √18 m. Qual é o perímetro aproximado dessa cerca?
a) 6,8 metros
b) 4,2 metros
c) 11 metros
d) 15 metros
e) 17,8 metros
Para calcular esse perímetro, temos que calcular primeiro os valores das raízes.
√48 = √(3·4·4) = √(3·42) = 4·√3
Como a raiz de três não é exata, é necessário fazer uma aproximação. Sabendo que √1 = 1 e que √4 = 2, então, √3 está entre 1 e 2. A melhor aproximação com uma casa decimal é 1,7. Então, para finalizar, basta multiplicar 4 por 1,7.
√48 = 4·√3 = 4·1,7 = 6,8
Fazendo o mesmo para √18, teremos:
√18 = √(3·3·2) = 3·√2 = 3·1,4 = 4,2
Para finalizar, calcule o perímetro da cerca pela soma de seus lados:
6,8 + 6,8 + 4,2 = 17,8 metros
Gabarito: letra E.
Das alternativas a seguir, qual é a melhor aproximação da raiz cúbica de 864?
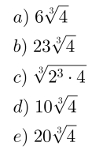
Para resolver esse problema, temos que decompor 864 em fatores primos. A decomposição é: 864 = 2·2·2·3·3·3·4. Agora basta calcular a raiz cúbica:
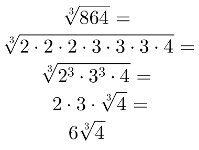
Gabarito: letra A.






