Exercícios sobre cilindro
Um reservatório cilíndrico está com \(3 \over 5\)da sua capacidade cheios de água. Sabendo que ele possui raio igual a 2 metros e altura de 10 metros, a quantidade de água que ainda cabe nesse reservatório, em litros, é igual a:
(Use π = 3.)
A) 120000
B) 72000
C) 64000
D) 48000
E) 12000
Alternativa D
Primeiramente, calcularemos o volume total do reservatório:
\(V=\pi\ r^2\cdot\ h\)
\(V=3\cdot2^2\cdot10\)
\(\ V\ =\ 3\ \cdot4\ \cdot10\ \)
\(V=120m^3\)
Sabendo que 35 estão cheios, então restam 25 . Fazendo o cálculo, temos:
\(\frac{2}{5}\cdot120=\frac{240}{5}=48\ m^3\)
Como na questão o volume é dado em litros, para converter m³ , uma unidade de medida diferente, basta multiplicar por 1000.
48 ⋅ 1000 = 48000 litros
Qual deve ser a altura de um cilindro para que ele tenha volume igual a 7850 cm³ e raio igual a 5 cm?
(Use \(\pi\) = 3,14.)
A) 100 cm
B) 120 cm
C) 140 cm
D) 150 cm
E) 180 cm
Alternativa A
\(V=\pi r^2\cdot h\)
\(7850=3,14\cdot5^2\cdot h\)
\(7850=\ 3,14\cdot25h\)
\(h=\frac{7850}{78,5}\)
\(7850\ =\ 78,5h\)
\(h\ =\ 100\ cm\)
Um galão no formato cilíndrico será reformado, e toda a sua parte externa será pintada. Sabendo que ele possui 1,2 metros de altura e raio igual a 40 centímetros, a área total desse galão é igual a:
(Use \(\pi\) = 3,1.)
A) 3,968 m³
B) 3,849 m³
C) 3,498 m³
D) 3,239 m³
E) 3,049 m³
Alternativa A
Inicialmente, temos:
h = 1,2 m
r = 40 cm = 0,4 m
A área total do cilindro é calculada por:
\(A=2\pi r\ \left(r+h\right)\)
\(A=2\cdot3,1\cdot0,4\ \left(0,4+1,2\right)\)
\(A\ =\ 2\cdot3,1\cdot0,4\ \cdot1,6\ \)
\(A\ =\ 3,968\ m^3\)
Qual é o volume de um cilindro cuja altura é igual ao dobro de seu raio.
a) πr3
b) 2r3
c) 2πr
d) 2π
e) 2πr3
Alternativa E
Se o raio desse cilindro mede x, então sua altura mede 2x. Logo:
V = πr2·h
V = πx2·2x
V = 2πr3
Dois cilindros possuem o mesmo volume. Sabendo que o primeiro possui diâmetro igual a 12 cm e o segundo, diâmetro igual a 16 cm, a relação entre a altura do primeiro cilindro e do segundo é igual a:
A) \(\ h_1=\frac{9}{16}h_2\)
B) \(\ h_1=\frac{16}{9}h_2\)
C) \(\ h_1=\frac{2}{3}h_2\)
D) \(\ h_1=\frac{3}{2}h_2\)
E) \(\ h_1=\frac{64}{9}h_2\)
Alternativa B
Sabemos que V1 = V2.
Dividindo os diâmetros pela metade, o primeiro cilindro possuirá raio igual a 6cm e o segundo, igual a 8cm. Logo, calculamos:
\(\pi\cdot6^2h_1=\pi\cdot8^2\cdot h_2\)
Simplificando \(\pi\) dos dois lados:
\(36h_1=64h_2\)
Isolando h1:
\(h_1=\frac{64}{36}h_2\)
\(h_1=\frac{16}{9}h_2\)
Analise a imagem a seguir:
O sólido geométrico que possui essa planificação é o(a):
A) prisma de base circular.
B) prisma de base retangular.
C) pirâmide de base circular.
D) cilindro.
E) cone.
Alternativa D
O sólido geométrico advindo dessa planificação é o cilindro.
Um porta-joias é feito no formato de cilindro, como na imagem a seguir:
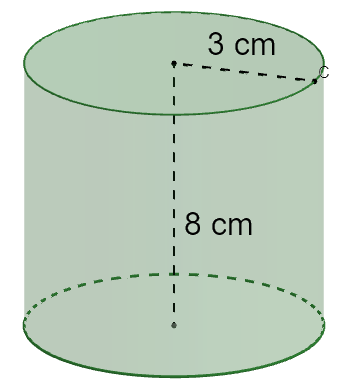
Podemos afirmar que a área total desse porta joias é de:
A) 99π cm³
B) 66π cm³
C) 33π cm³
D) 18π cm³
E) 11π cm³
Alternativa B
Calculando a área total:
\(A=2\pi r\ \left(r+h\right)\)
\(A=2\pi\cdot3\ \left(3+8\right)\)
\(A\ =\ 2\cdot3\ \cdot11\pi\)
\(A=66\pi cm^3\)
Sobre o cilindro, julgue as afirmativas a seguir.
I – O cilindro é classificado como poliedro.
II – O cilindro é um prisma de base circular.
III – A planificação do cilindro é composta por dois círculos de raios iguais e um retângulo.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são falsas.
Alternativa C
I – Falsa
O cilindro não é um poliedro, e sim um corpo redondo.
II – Falsa
O cilindro não é um prisma, pois este possui bases formadas por polígonos.
III – Verdadeira
Essas são as características da planificação de um cilindro.
Analisando o cilindro a seguir, podemos afirmar que o seu volume é igual a:
(Use \(\pi\) = 3.)
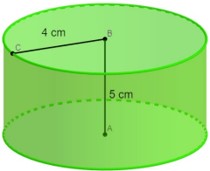
A) 150 cm³
B) 180 cm³
C) 210 cm³
D) 240 cm³
E) 250 cm³
Alternativa D
Calculando o volume:
\(V=\pi\cdot r^2\cdot h\)
\(V=3\cdot4^2\cdot5\)
\(V\ =\ 3\cdot16\ \cdot5\)
\(V=240cm^3\)
(Enem 2012 – PPL) Uma prefeitura possui modelos de lixeira de forma cilíndrica, sem tampa, com raio medindo 10 cm e altura de 50 cm. Para fazer uma compra adicional, solicita à empresa fabricante um orçamento de novas lixeiras, com a mesma forma e outras dimensões. A prefeitura só irá adquirir as novas lixeiras se a capacidade de cada uma for no mínimo dez vezes maior que o modelo atual e seu custo unitário não ultrapassar R$ 20,00. O custo de cada lixeira é proporcional à sua área total e o preço do material utilizado na sua fabricação é de R$ 0,20 para cada 100 cm². A empresa apresenta um orçamento discriminando o custo unitário e as dimensões, com o raio sendo o triplo do anterior e a altura aumentada em 10 cm.
(Aproxime π para 3.)
O orçamento dessa empresa é rejeitado pela prefeitura, pois
A) o custo de cada lixeira ficou em R$ 21,60.
B) o custo de cada lixeira ficou em R$ 27,00.
C) o custo de cada lixeira ficou em R$ 32,40.
D) a capacidade de cada lixeira ficou 3 vezes maior.
E) capacidade de cada lixeira ficou 9 vezes maior.
Calculando o volume da lixeira atual:
\(V=\pi r^2\cdot h\)
\(V=3\cdot{10}^2\cdot50\)
\(V\ =\ 3\cdot100\cdot50\ \)
\(V=\ 15000\ cm^3\)
Já a nova lixeira precisa ter uma capacidade de pelo menos 10 vezes o volume da lixeira atual, ou seja, 150000 cm³. Além disso, o seu custo deve ser no máximo de R$ 20,00.
O volume da nova lixeira é igual a:
\(V=\pi r^2\cdot h\)
\(V=3\cdot{30}^2\cdot60\)
\(V\ =\ 3\cdot900\cdot60\ \)
\(V=162000cm^3\)
Note, então, que o volume é maior que 150000 cm³, satisfazendo a capacidade desejada. Agora, calcularemos o custo dessa lixeira. Para isso, é necessário descobrir a sua área total. Como ela não tem tampa, a sua área será a soma da área base, que é um círculo, ou seja, πr2 , mais a sua área lateral, que é igual a \(2\pi r\cdot h:\)
\(A=\pi r^2+2\pi r\cdot h\)
\(A=3\cdot{30}^2+2\cdot3\cdot30\cdot60\)
\(A\ =\ 2700\ +\ 10900\)
\(A\ =\ 13500\ cm^2\)
Sabemos que cada 100 cm² custa R$ 0,20, então o custo dessa lixeira é igual a:
C = \(\frac{13500}{100}\cdot0,2\)
\(C=\ 135\ \cdot0,2\ \)
\(C\ =\ 27,00\)
O custo de cada lixeira ficou em R$ 27,00.
(Enem 2020 — PPL) Um piscicultor cria uma espécie de peixe em um tanque cilíndrico. Devido às características dessa espécie, o tanque deve ter, exatamente, 2 metros de profundidade e ser dimensionado de forma a comportar 5 peixes para cada metro cúbico de água. Atualmente, o tanque comporta um total de 750 peixes. O piscicultor deseja aumentar a capacidade do tanque para que ele comporte 900 peixes, mas sem alterar a sua profundidade. Considere 3 como aproximação para π.
O aumento da medida do raio do tanque, em metro, deve ser de
A) \(\sqrt{30}-5\)
B) \(\frac{\sqrt{30}-5}{2}\)
C) \(\sqrt5\)
D) \(\frac{5}{2}\)
E) \(\frac{15}{2}\)
Alternativa A
Sabemos que há uma capacidade para 750 peixes. Considerando que há 5 peixes para cada m³, há 750 : 5 = 150 m³ de volume, inicialmente.
Dessa forma, calculamos:
\(V_i=150\)
\(\pi\cdot r^2\cdot h=150\)
\(3\cdot r^2\cdot2=150\)
\(6x^2=150\)
\(r^2=\frac{150}{6}\)
\(r^2=25\)
\(r=\sqrt{25}\)
\(r=5\ \)
O raio era, inicialmente, de 5 metros.
Com o aumento, no novo tanque caberão 900 peixes. 900 : 5 = 180 m³.
Sabendo que o volume novo é de 180 m³:
\(V_n=180\)
\(V_n=3\cdot r_n^2\cdot2=180\)
\(r_n^2=\frac{180}{6}\)
\(r_n=\sqrt{30}\)
Assim, a diferença entre o raio novo e o raio inicial é de:
\(\sqrt{30}-5\)
(Enem 2020) Uma loja de materiais de construção vende dois tipos de caixas-d’água: tipo A e tipo B. Ambas têm formato cilíndrico e possuem o mesmo volume, e a altura da caixa-d’água do tipo B é igual a 25% da altura da caixa-d’água do tipo A.
Se R denota o raio da caixa-d’água do tipo A, então o raio da caixa-d’água do tipo B é
A) \( \frac{R}{2}\)
B) 2R
C) 4R
D) 5R
E) 16R
Alternativa B
Sabemos que:
hb = 0,25 ha
Da mesma forma, sabemos que os volumes são iguais. Dessa forma, obtemos:
\(\pi R^2\cdot h_a=\pi\cdot r_b^2h_b\)
Simplificando \(\pi \) dos dois lados e substituindo hb = 0,25 ha:
\(R^2\cdot\ h_a=r_b^2\cdot0,25h_a\)
Simplificando \(h_a \) em ambos os lados:
\(R^2=r_b^2\cdot0,25\)
\(R^2=\sqrt{r_b^2\cdot0,25}\)
\(R=0,5r_b\)
Representando 0,5 como uma fração:
\(R=\frac{1}{2}r_b\)
\(2R=r_b\)
(Enem 2015 – PPL) Uma fábrica brasileira de exportação de peixes vende para o exterior atum em
conserva, em dois tipos de latas cilíndricas: uma de altura igual a 4 cm e raio 6 cm e outra de altura desconhecida e raio de 3 cm, respectivamente, conforme figura. Sabe-se que a medida do volume da lata que possui raio maior, V1, é 1,6 vezes a medida do volume da lata que possui raio menor, V2.
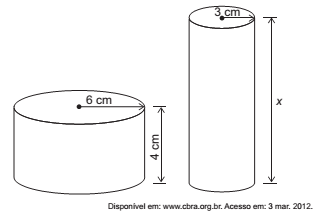
A medida da altura desconhecida vale
A) 8 cm
B) 10 cm
C) 16 cm
D) 20 cm
E) 40 cm
Alternativa B
Calando o volume V1:
\(V_1=\pi\cdot6^2\cdot4\ \)
\(V_1=144\)
Calculando V2:
\(V_2=\pi\cdot3^2\cdot h\ \)
\(V_2=9\pi h\)
Como V1 = 1,6V2:
\(144\pi=1,6\ \cdot\ 9\pi h\)
\(144\ =\ 14,4h\)
\(h=\frac{144}{14,4}\)
\(h\ =10\)
