Exercícios de teorema de Stevin
(Unipac) Uma prensa hidráulica possui pistões com diâmetros de 10 cm e 20 cm. Se uma força de 120 N atua sobre o pistão menor, pode-se afirmar que essa prensa estará em equilíbrio quando sobre o pistão maior atuar uma força de:
a) 30 N
b) 60 N
c) 480 N
d) 240 N
e) 120 N
Letra A.
Primeiramente, calcularemos o raio do pistão maior, por meio do seu diâmetro:
\(r_1=\frac{d_1}2\)
\(r_1=\frac{20}2\)
\(r_1=10\ cm\)
E o raio do pistão menor:
\(r_2=\frac{d_2}2\)
\(r_2=\frac{10}2\)
\(r_2=5\ cm\)
Depois, calcularemos a área do pistão maior:
\(A_1=π\cdot r_1^2\)
\(A_1=π\cdot 10^2\)
\(A_1=100π\ cm^2 \)
E a área do pistão menor:
\(A_2=π\cdot r_2^2\)
\(A_2=π\cdot 5^2\)
\(A_2=25π\ cm^2\)
Por fim, substituiremos os dados na fórmula do teorema de Pascal:
\(\frac{F_1}{A_1} =\frac{F_2}{A_2} \)
\(\frac{120}{100π}=\frac{F_2}{25π}\)
\(F_2=\frac{120\cdot 25π}{100π}\)
\(F_2=30\ N\)
(PUC-RS) No oceano a pressão hidrostática aumenta aproximadamente uma atmosfera a cada 10 m de profundidade. Um submarino encontra-se a 200 m de profundidade, e a pressão do ar no seu interior é de uma atmosfera. Nesse contexto, pode-se concluir que a diferença da pressão entre o interior e o exterior do submarino é, aproximadamente, de
a) 200 atm
b) 100 atm
c) 21 atm
d) 20 atm
e) 19 atm
Letra D.
De início, calcularemos a pressão externa usando o teorema de Stevin:
\(∆p=p-p_o\)
Lembrando que \(p_o\) é a pressão atmosférica, p é a pressão absoluta, que nesse caso se trata da pressão externa \(p_e\), e \(∆p \) é a pressão manométrica, que nesse caso se trata da pressão hidrostática \(p_h\).
\(p_h=p_e-p_o\)
\(p_e=p_h+p_o\)
De acordo com o enunciado, a cada 10 metros a pressão hidrostática aumenta 1 atm, então a uma profundidade de 200 metros, a pressão hidrostática é 20 atm e a pressão atmosférica é 1 atm. Assim, a pressão externa é:
\(p_e=p_h+p_o\)
\(p_e=20+1\)
\(p_e=21\ atm\)
Por fim, calcularemos a diferença de pressão no interior e no exterior do submarino, sabendo que a pressão interna é 1 atm:
\(∆p=p_e-p_i\)
\(∆p=21-1\)
\(∆p=20\ atm\)
(Udesc) Certa quantidade de água é colocada em um tubo em forma de U, aberto nas extremidades. Em um dos ramos do tubo, adiciona-se um líquido de densidade maior que a da água, e ambos não se misturam.
Assinale a alternativa que representa corretamente a posição dos dois líquidos no tubo após o equilíbrio.
Letra D.
Ao se colocar líquidos a diferentes densidades em um recipiente em U, eles terão alturas diferentes, ainda que apresentem a mesma pressão. Como a densidade da água é menor que a densidade do líquido, a altura da água deve ser maior que a altura do líquido.
(UFF-RJ) O sifão é um instrumento usado para a retirada de água de lugares de difícil acesso.
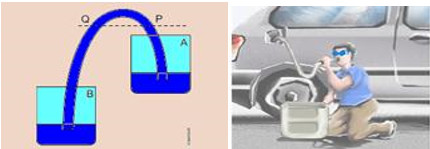
Como mostra a figura a seguir, seu funcionamento se baseia no fato de que, quando o tubo que liga os recipientes A e B está cheio, há uma diferença de pressão hidrostática entre os pontos P e Q, o que provoca um fluxo de água de A para B. Essa diferença de pressão depende da seguinte característica do nosso planeta:
a) pressão atmosférica.
b) aceleração da gravidade local.
c) temperatura da superfície.
d) densidade da atmosfera.
e) velocidade de rotação do planeta.
Letra B.
Podemos analisar essa questão por meio da fórmula do teorema de Stevin:
\(∆p=d\cdot g\cdot ∆h\)
De acordo com o teorema, a variação de pressão hidrostática depende da densidade do líquido, da aceleração da gravidade local e da variação de altura.
Quando se aplica uma força de 300 N sobre o menor pistão de uma prensa hidráulica, com raio de 0,4 metros, ocorrerá uma força sobre o pistão maior, com raio de 0,8 metros, com valor de:
a) 300 N
b) 600 N
c) 900 N
d) 1200 N
e) 2400 N
Letra D.
Inicialmente, calcularemos a área do pistão maior:
\(A_1=π\cdot r_1^2\)
\(A_1=π\cdot 0,4^2\)
\(A_1= 0,16π\ m^2\)
E a área do pistão menor:
\(A_2=π\cdot r_2^2\)
\(A_2=π\cdot 0,8^2\)
\(A_2=0,64π\ m^2\)
Por fim, substituiremos os dados na fórmula do teorema de Pascal:
\(\frac{F_1}{A_1} =\frac{F_2}{A_2} \)
\(\frac{300}{0,16π}=\frac{F_2}{0,64π}\)
\(F_2=\frac{300\cdot 0,64π}{0,16π}\)
\(F_2=1200\ N\)
Calcule a variação de pressão sobre um mergulhador que está a uma profundidade de 0,5 metros, sabendo que a densidade da água é 1000 kg/m e a aceleração da gravidade é \(10\ m/s^2\).
a) \(3\cdot 10^3\ Pa\)
b) \(4\cdot 10^3\ Pa\)
c) \(5\cdot 10^3\ Pa\)
d) \(6\cdot 10^3\ Pa\)
e) \(7\cdot 10^3\ Pa\)
Letra C.
Calcularemos a variação de pressão sobre o mergulhador usando o teorema de Stevin:
\(∆p=d\cdot g\cdot ∆h\)
\(∆p=1000\cdot 10\cdot 0,5\)
\(∆p=5000\)
\(∆p=5\cdot 10^3\ Pa\)
Calcule a altura atingida pela água quando ela é despejada em um recipiente em formato de U que contém óleo e que após o equilíbrio tem uma altura de 0,8 metros, sabendo que a densidade da água é \(1000\ kg/m^3\) e do óleo é \(800\ kg/m^3\).
a) 1,00 m
b) 0,32 m
c) 0,50 m
d) 0,80 m
e) 0,64 m
Letra E.
Calcularemos a altura atingida pela água por meio da fórmula do princípio dos vasos comunicantes:
\(\frac{H_1}{H_2} =\frac{d_2}{d_1} \)
\(\frac{H_1}{0,8}=\frac{800}{1000}\)
\(H_1=\frac{0,8\cdot 800}{1000}\)
\(H_1=0,64\ m\)
Calcule a área do pistão maior de uma prensa hidraúlica que recebe uma força de 200 N, sabendo que sobre o pistão menor de \(2\ m^2\) é aplicada uma força de 80 N.
a) \(2\ m^2 \)
b) \(3\ m^2 \)
c) \(4\ m^2 \)
d) \(5\ m^2 \)
e) \(6\ m^2 \)
Letra D.
Calcularemos a área do pistão maior, usando o teorema de Pascal:
\(\frac{F_1}{A_1} =\frac{F_2}{A_2} \)
\(\frac{80}{2}=\frac{200}{A_2} \)
\(A_2=\frac{200\cdot 2}{80}\)
\(A_2=5\ m^2\)
Após seus estudos a respeito do Teorema de Stevin, determine quais das proposições abaixo são consideradas suas aplicações:
I) Princípio de Bernoulli.
II) Teorema de Arquimedes.
III) Vasos comunicantes.
IV) Teorema de Pascal.
a) Alternativas I e II.
b) Alternativas III e IV.
c) Alternativas I e III.
d) Alternativas II e IV.
e) Alternativas I e IV.
Letra B. Os vasos comunicantes e o teorema de Pascal são aplicações do teorema de Stevin, já que ele propiciou o desenvolvimento deles.
Qual a profundidade máxima que um nadador pode alcançar sabendo que o seu pulmão suporta uma diferença de pressão de 0,08 atm? Considere que a densidade da água é 1000 kg/m e a aceleração da gravidade é \(10\ m/s^2\).
a) 0,08106 m
b) 0,008106 m
c) 0,8106 m
d) 8,106 m
e) 81,06 m
Letra C.
Primeiramente, transformaremos a pressão de atm para Pascal:
0,08 atm = 8106 Pa
Depois, calcularemos a profundidade máxima atingida pelo nadador por meio do teorema de Stevin:
\(∆p=d\cdot g\cdot ∆h\)
\(8106=1000\cdot 10\cdot ∆h\)
\(∆h=\frac{8106}{1000\cdot 10}\)
\(∆h=0,8106\ m\)
Calcule a densidade do líquido que é despejado em um recipiente contendo mercúrio, cuja densidade é \(13,534\ g/m^3\), sabendo que o líquido está a uma altura de 30 cm e o mércurio, a 90 cm.
a) \(40,602\ g/m^3\)
b) \(50,786\ g/m^3\)
c) \(60,902\ g/m^3\)
d) \(70,413\ g/m^3\)
e) \(80,258\ g/m^3\)
Letra A.
De início, converteremos as alturas de centímetros para metros:
30 cm = 0,3 m
90 cm = 0,9 m
Depois, calcularemos a densidade do líquido usando a fórmula do princípio dos vasos comunicantes:
\(\frac{H_1}{H_2} =\frac{d_2}{d_1} \)
\(\frac{0,3}{0,9}=\frac{13,534}{d_1} \)
\(d_1=\frac{13,534\cdot 0,9}{0,3}\)
\(d_1=40,602\ g/m^3\)
Quais proposições apresentam a unidade de medida correspondente à grandeza física estudada no teorema de Stevin?
I) A densidade é medida em \(kg/m^3\).
II) A altura é medida em Pascal.
III) A pressão é medida em metros por segundo.
IV) A força é medida em Newton.
a) Alternativas I e II.
b) Alternativas III e IV.
c) Alternativas I e III.
d) Alternativas II e IV.
e) Alternativas I e IV.
Letra E.
Abaixo, vemos a correção, em vermelho, das alternativas incorretas.
I) Correta.
II) Incorreta. A altura é medida em metros.
III) Incorreta. A pressão é medida em Pascal.
IV) Correta.
