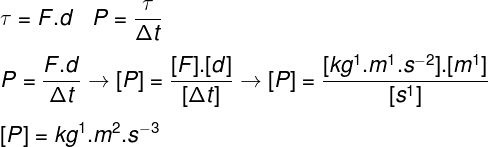Exercícios sobre análise dimensional
Uma grandeza física W é definida pela expressão [W] = [L]-2[M]3[T]². A unidade de medida de W, de acordo com o S.I., é:
a) s-³m-2kg-1
b) s-2m3kg-³
c) m2kg-3K²
d) m2kg3s²
e) m-2kg3s²
Letra E
Para encontrarmos a grandeza física relacionada a W, precisamos lembrar-nos de que L trata-se de um comprimento (m), m é uma massa (kg) e T é um tempo (s). Dessa forma, a unidade de W será [W] = [m]-².[kg]³.s².
A unidade de medida da grandeza densidade, definida pela razão entre massa e volume, nas unidades do S.I., é igual a:
a) m.kg-3
b) kg-1.m-2
c) kg.m-3
d) m-2.g2
e) mg-1.m-3
Letra C
A unidade de medida da densidade é dada pela razão entre as unidades de massa e volume. De acordo com o S.I., a unidade de massa é o kg, enquanto a unidade de volume deve ser o m³, portanto, a unidade de medida de densidade deve ser [d] = [kg].[m-3].
Uma unidade derivada, escrita de acordo com o S.I., tem a sua unidade dada em kg¹.m¹.s-2. Assinale a alternativa que apresenta corretamente qual é essa unidade derivada:
a) Pascal
b) Newton
c) Ampére
d) Joule
e) Coulomb
Letra B
A unidade física que deriva do kg¹.m¹.s-2 é o Newton. Basta lembrarmo-nos da expressão da segunda lei de Newton: F = m.a. De acordo com o S.I., a massa do corpo deve ser medida em kg, enquanto sua aceleração deve ser informada em m/s².
A grandeza física potência, medida em Watts, nas unidades do S.I., mede a quantidade de trabalho, em Joules, que é realizado a cada segundo. A unidade Watt também pode ser escrita como:
a) kg-1.m-2.s3
b) kg-2.m2.s-3
c) kg1.m2.s-3
d) kg1.m-2.s3
e) kg-3.m-2.s3
Letra C
Para respondermos a essa questão, é necessário que nos lembremos de como é a expressão do trabalho e da potência, observe a figura:
