Exercícios sobre operações com vetores
(UFPI) A resultante dos vetores \(\vec{v_1}\) e \(\vec{v_2}\) é melhor representada por:
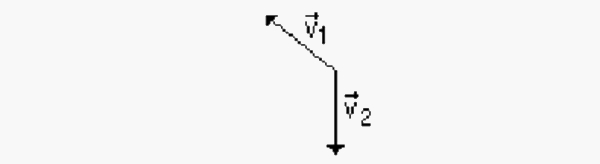
A) 
B) 
C) 
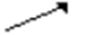
D) 
E) 
Alternativa A.
O vetor resultante da operação com esses vetores terá orientação diagonal a sudoeste.
(Unifor - Adaptada) A soma de dois vetores de módulos 12N e 18N tem certamente módulo de valor:
A) 6 N.
B) 30 N.
C) 12 N .
D) 18 N.
E) 31 N.
Alternativa B.
Calcularemos o tamanho do vetor resultante realizando a soma de vetores que estão na mesma direção:
\(\vec{R} = \vec{v} + \vec{u}\)
\(\vec{R} =12+18\)
\(\vec{R} =30 N\)
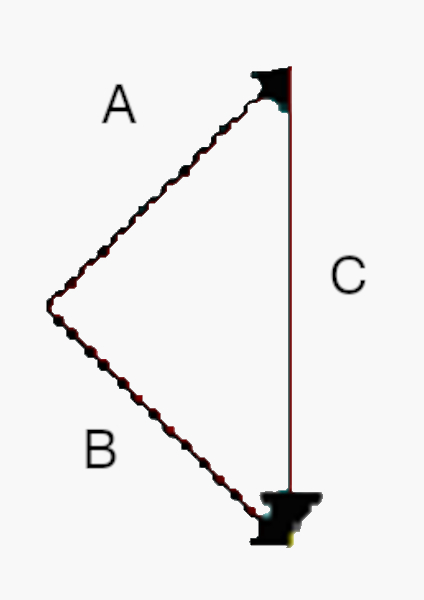
(UFMG) Dado o diagrama, pergunta-se qual a expressão correta:
A) \(\vec{B} + \vec{C} = \vec{A} \)
B) \(\vec{A} + \vec{B} = \vec{C}\)
C) \(\vec{C} - \vec{B} = \vec{A}\)
D) \(\vec{B} - \vec{A} = \vec{C}\)
E) \(\vec{A} - \vec{B} = \vec{C} \)
Alternativa D.
A expressão correta para a representação da figura é dada pela expressão:
\(\vec{B} - \vec{A} = \vec{C}\)
(Ufal) A localização de um lago, em relação a uma caverna pré-histórica, exigia que se caminhasse 200 m numa certa direção e, a seguir, 480 m numa direção perpendicular à primeira. A distância em linha reta, da caverna ao lago era, em metros,
A) 680.
B) 600.
C) 540.
D) 520.
E) 500.
Alternativa D.
Calcularemos a distância em linha reta (que corresponde à hipotenusa do triângulo) por meio da soma de vetores perpendiculares, a partir da fórmula do teorema de Pitágoras:
vetor resultante2 = a2 + b2
vetor resultante2 = 2002 + 4802
vetor resultante2 = 40 000 + 230 400
vetor resultante2 = 270 400
vetor resultante = \(\sqrt{270\,400}\)
vetor resultante = 520
Calcule o vetor resultante da subtração de um vetor \(\vec{v} \) com módulo de 9 unidades de um vetor \(\vec{u} \) com módulo de 2 unidades.
A) 2 u
B) 5 u
C) 7 u
D) 9 u
E) 11 u
Alternativa C.
Calcularemos o tamanho do vetor resultante realizando a subtração de vetores que estão na mesma direção:
\(\vec{R} = \vec{v} + \vec{u} \)
\(\vec{R} = 9 - 2 \)
\(\vec{R} = 7 \ u\)
Calcule o vetor resultante da soma entre dois vetores oblíquos com módulos de 3 unidades e de 4 unidades, sabendo que o ângulo entre eles é de 60°.
A) 0,93 u
B) 1,78 u
C) 2,04 u
D) 3,65 u
E) 4,12 u
Alternativa E.
Calcularemos o tamanho do vetor resultante (que corresponde à hipotenusa) por meio da soma de vetores oblíquos, a partir da fórmula da lei dos cossenos:
\(\text{hipotenusa}^2 = \text{cateto}_1^2 + \text{cateto}_2^2 - 2 \cdot \text{cateto}_1 \cdot \text{cateto}_2 \cdot \cos \theta \)
\(R^2 = u^2 + v^2 - 2 \cdot u \cdot v \cdot \cos \theta \)
\(R^2 = 3^2 + 4^2 - 2 \cdot 2 \cdot 4 \cdot \cos 60^\circ \)
\(R^2 = 9 + 16 - (16 \cdot 0,5) \)
\(R^2=9+16-8\)
\(R^2=17\)
\(R = \sqrt{17} \)
\(R \cong 4,12 u\)
O vetor resultante da multiplicação de um número real n por um vetor de 5 unidades tem 6,6 unidades. Com base nessas informações, qual o valor do número real?
A) 1,32
B) 2,63
C) 3,87
D) 4,15
E) 5,96
Alternativa A.
Calcularemos o número real a partir da fórmula da multiplicação de um número real por um vetor:
\(v_{\text{novo}} = n \cdot \vec{v} \)
\(6,6=n \cdot 5\)
\(n = \frac{6,6}{5} \)
\(n=1,32\)
Determine o tamanho do vetor resultante da soma de um vetor \(\vec{a}\) de 125 unidades com um vetor \(\vec{b} \) de 32 unidades, sabendo que os vetores estão na mesma direção e no mesmo sentido.
A) 24 u
B) 63 u
C) 89 u
D) 157 u
E) 325 u
Alternativa D.
Calcularemos o tamanho do vetor resultante realizando a soma de vetores que estão na mesma direção:
\(\vec{R} = \vec{a} + \vec{b} \)
\(\vec{R} = 125 + 32 \)
\(\vec{R} = 157\,\mathbf{u} \)
Qual o tamanho do vetor resultante da soma de um vetor \(\vec{v} \) de 15 unidades com um vetor \(\vec{u} \) de 6 unidades, sabendo que os vetores estão na mesma direção e no mesmo sentido?
A) 10 u
B) 21 u
C) 32 u
D) 43 u
E) 54 u
Alternativa B.
Calcularemos o tamanho do vetor resultante realizando a soma de vetores que estão na mesma direção:
\(\vec{R} = \vec{v} + \vec{u} \)
\(\vec{R} = 15 + 6 \)
\(\vec{R} = 21 \ u \)
Dois vetores com módulos de 12 unidades e de 5 unidades são perpendiculares em um plano cartesiano. Qual o módulo do vetor resultante da soma desses vetores?
A) \(1\sqrt{5} \ u \)
B) \(5\sqrt{2} \ u \)
C) \(10\sqrt{3} \ u \)
D) \(15\sqrt{2} \ u \)
E) \(24\sqrt{3} \ u \)
Alternativa C.
Calcularemos o módulo do vetor resultante realizando a soma de vetores perpendiculares:
\(\text{hipotenusa}^2 = \text{cateto}_1^2 + \text{cateto}_2^2\)
\(R^2=u^2+v^2\)
\(R^2=12^2+5^2\)
\(R^2=144+25\)
\(R^2=300\)
\(R = \sqrt{300} \)
\(R = \sqrt{3 \cdot 100} \)
\(R = 10 \sqrt{3}\ u \)
Determine o vetor resultante da subtração entre um vetor de 15 unidades e um de 50 unidades, lembre-se que o sinal negativo é apenas um indicativo do sentido do vetor.
A) 15 u
B) 20 u
C) 25 u
D) 30 u
E) 35 u
Alternativa E.
Calcularemos o tamanho do vetor resultante realizando a subtração de vetores que estão na mesma direção:
\(\vec{R} = \vec{v} - \vec{u} \)
\(\vec{R} = 15 - 50\)
\(\vec{R} = -35\,\mathbf{u} \)
Um vetor \(\vec{u} \) de módulo de 4 unidades é multiplicado pelo número real 200. Qual o tamanho do vetor resultante dessa operação?
A) 100 u
B) 200 u
C) 400 u
D) 600 u
E) 800 u
Alternativa E.
Calcularemos o tamanho do vetor resultante realizando a multiplicação do número real pelo tamanho do vetor u :
\(v_{\text{novo}} = n \cdot \vec{v} \)
\(v_{\text{novo}} = 200 \cdot 4 \)
\(v_{novo}=800 u\)
