Home
Exercícios de Física
Exercícios sobre movimento circular uniformemente variado (MCUV)

Exercícios sobre movimento circular uniformemente variado (MCUV)

Esta lista de exercícios testará seus conhecimentos em relação ao conteúdo de movimento circular uniformemente variado e suas aplicações cotidianas. Publicado por: Gustavo Campos

Imprimir

Questão 1

Em uma corrida, 3 competidores (A, B e C) estão paralelamente alinhados e com a mesma velocidade de 6 m/s, em uma parte do trajeto que é circular. Considere que o raio da curva do competidor A é maior que o raio da curva do competidor B, que este está em um raio maior do que o do competidor C (R_A > R_B >R_C) e que os três possuem a mesma aceleração nesse momento.

a) O competidor A completará primeiro essa etapa do trajeto, porque terá a maior aceleração angular.

b) O competidor B completará primeiro essa etapa do trajeto, porque terá a maior aceleração angular.

c) O competidor C completará por último essa etapa do trajeto, porque terá a menor aceleração angular.

d) O competidor A completará por último essa etapa do trajeto, porque terá a menor aceleração angular.

e) O competidor completará por último essa etapa do trajeto, porque terá a menor aceleração angular.

Ver resposta

Resposta

Letra D

A aceleração angular é inversamente proporcional ao raio do trajeto. Logo, se os três estão alinhados e com a mesma velocidade, o fator que irá diferenciá-los será a aceleração angular, que por sua vez depende do raio. Como o competidor A é aquele que forma o maior raio, sua aceleração angular será a menor.

Questão 2

Durante uma viagem, um carro que se move com velocidade constante de 18 m/s passa por um trajeto curvilíneo de 6 m de raio, concluindo-o com velocidade de 21 m/s em 1,25 segundos. A variação da velocidade angular e a aceleração angular do carro nessa etapa são iguais a:

a) 0,5 rad/s e 0,4 rad/s²

b) 12 rad/s e 5 rad/s²

c) 3 rad/s e 10 rad/s²

d) 15 rad/s e 6 rad/s²

e) 3 rad/s e 5 rad/s²

Ver resposta

Resposta

Letra A

A variação da velocidade angular Δω equivale à razão Δv, que é a diferença entre a velocidade final e inicial linear e o raio da curva.

$∆ω=\frac{∆v}R=\frac{21-18}6=\frac36=0,5\ rad/s$

$\alpha=\frac{∆ω}t=\frac{0,5}{1,25}=0,4\ rad/s²$

Questão 3

Uma supercentrífuga foi fabricada por encomenda para um determinado laboratório para a separação de substâncias muito densas. Ela tem como característica principal um programa que possibilita que sua velocidade aumente gradativamente até atingir o ápice de 300 rad/s. Ela atinge sua velocidade máxima após 20 voltas completas, iniciando a programação desde o repouso. Escolha a alternativa que representa a aceleração angular, em rad/s², da supercentrífuga.

Utilize π = 3.

a) 12

b) 20

c) 1,5

d) 6

e) 10

Ver resposta

Resposta

Letra C

ω_o = 0

ω = 60 rad/s

Δθ = 20 voltas

α = ?

Para 20 voltas completas, há o deslocamento angular. Logo, se uma volta equivale a 2πrad, 20 voltas equivalem a esse valor multiplicado por 20, 40πrad. O problema não mencionou o tempo. Analisando os valores fornecidos, conclui-se que a equação que melhor se encaixa é a de Torricelli para o MCUV.

O problema permite considerar π = 3, então:

Δθ = 40πrad = 40 · 3 = 120 rad

$\omega^2=\omega_0^2+2·α·∆θ$

${60}^2=0^2+2·α·120$

3600 = 240 · α

$\alpha=\frac{3600}{240}=1,5\ rad/s²$

Questão 4

(Enem 2019) Na madrugada de 11 de março de 1978, partes de um foguete soviético reentraram na atmosfera acima da cidade do Rio de Janeiro e caíram no oceano Atlântico. Foi um belo espetáculo. Os inúmeros fragmentos entrando em ignição devido ao atrito com a atmosfera brilharam intensamente, enquanto “cortavam o céu”. Mas se a reentrada tivesse acontecido alguns minutos depois, teríamos uma tragédia, pois a queda seria na área urbana do Rio de Janeiro, e não no oceano.

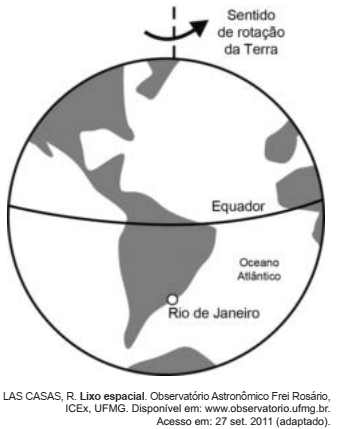
Representação do globo terrestre e do local onde foguete soviético entrou na atmosfera.

De acordo com os fatos relatados, a velocidade angular do foguete em relação à Terra no ponto de reentrada era

a) igual à da Terra e no mesmo sentido.

b) superior à da Terra e no mesmo sentido.

c) inferior à da Terra e no sentido oposto.

d) igual à da Terra e no sentido oposto.

e) superior à da Terra e no sentido oposto.

Ver resposta

Resposta

Letra B

A velocidade angular deve ser superior. Caso fosse igual, no momento da entrada do foguete na atmosfera, bem acima da cidade, o giro de ambos (foguete e planeta) coincidiria, ocasionando a queda dos pedaços do foguete na cidade. Além disso, se a velocidade angular do foguete fosse no sentido contrário ao da Terra, a cidade do Rio não seria acertada, mas alguma outra cidade brasileira, sim. Indo no sentido inverso do movimento terrestre, os destroços atingiriam o interior do país.

Questão 5

Em uma curva de raio R, um carro que iniciou a curva com velocidade de 6 rad/s manteve uma aceleração de 4 rad/s² durante 4 segundos, percorrendo um total de 112 metros. Considerando o início da curva como o ponto zero, o valor de R é:

a) 5 m

b) 10 m

c) 11 m

d) 2 m

e) 15 m

Ver resposta

Resposta

Letra D

ω_o = 6 rad/s
α = 4 rad/s²
θ₀ = 0
t = 4 s
R = ?
ΔS = 112 m

Para descobrir o raio da curva, é necessário saber o deslocamento angular, que nesse caso, como o ângulo inicial é zero, terá o mesmo valor que o ângulo final.

$\theta=\theta_0+\omega_0·t+\frac{α·t²}2$

$\theta=0+6·4+\frac{4.4^2}2$

$\theta=24+\frac{4·16}2=24+\frac{64}2=24+32=56\ rad$

$\theta=∆θ=\frac{∆S}R$

$56=\frac{112}{R}$

Como R está isolado no denominador, ele trocará de lugar com o 112.

$R=\frac{112}{56}=2\ m$

Questão 6

Um marceneiro aceitou fazer um guarda-roupa para uma determinada família utilizando um tipo de madeira rústico. Para o trabalho, ele usou uma furadeira que faz a broca rotacionar a uma velocidade de 6000 rad/s girando livremente. Quando ele utilizou a mesma furadeira na madeira, após 30 segundos de uso, à medida que a broca adentrou no material, sua velocidade mudou para 4500 rad/s. Com isso, a aceleração da furadeira passou a ser:

a) 50 rad/s²

b) 10 rad/s²

c) -50 rad/s²

d) -20 rad/s²

e) -10 rad/s²

Ver resposta

Resposta

Letra C

ω₀ = 6000 rad/s
ω = 4500 rad/s
t = 30 s
α = ?

$\omega=\omega_0+\alpha·t$

$4500=6000+\alpha·30$

$4500-6000=\alpha·30$

$-1500=\alpha·30$

$\alpha.30=-1500$

$\alpha=\frac{-1500}{30}=-50\ rad/s^2$

Questão 7

Um motociclista percorreu um trajeto circular obedecendo à seguinte função no SI:

ω = 12 + 3 · t

Considerando o início do trajeto como ponto zero, calcule o deslocamento angular que ocorreu até a velocidade de 42 rad/s ser atingida.

a) 270 rad

b) 600 rad

c) 800 rad

d) 180 rad

e) 500 rad

Ver resposta

Resposta

Letra A

Primeiramente, é preciso descobrir o tempo necessário para a velocidade de 42 rad/s ser atingida.

$\omega=12+3·t$

$42=12+3·t$

$42-12=3·t$

$30=3·t$

$3·t=30$

$t=\frac{30}{3}=10s$

Considerando que o ângulo inicial é zero, utiliza-se a função horária da posição.

$\theta=\theta_0+\omega_0·t+\frac{α·t^2}2$

$\theta=12·10+\frac{3·10^2}2=120+\frac{3·100}2=120+\frac{300}2=120+150=270\ rad$

Questão 8

Uma criança está segurando a extremidade de uma corda, e na outra extremidade há uma bolinha amarrada. Ela começa rodar a corda, girando cada vez mais rápido, mantendo inconscientemente uma aceleração de 4 rad/s². O tempo necessário para um deslocamento angular de 288 radianos é de:

a) 8 segundos

b) 20 segundos

c) 12 segundos

d) 60 segundos

e) 10 segundos

Ver resposta

Resposta

Letra C

α = 4 rad/s²
θ = 288 rad
t = ?

Como o exercício não detalhou o início do movimento, deduz-se que o ângulo inicial e a velocidade inicial sejam nulos.

$\theta=\theta_0+\omega_0·t+\frac{α·t^2}2$

$288=0+0·t+\frac{4·t^2}2$

$288=\frac{4·t^2}2$

$288=2·t^2$

$2·t^2=288$

$t^2=\frac{288}{2}$

$t^2=144$

Como o t está elevado ao quadrado, acrescenta-se a raiz quadrada em ambos os lados da equação para anular o expoente.

$\sqrt{t^2}=\sqrt{144}$

$t=12s$

Questão 9

Uma roda gigante possui 80 metros de diâmetro e, durante um turno do passeio, tem velocidade constante de 0,02 rad/s. Ao final do passeio, ela gasta um total de 40 segundos para parar totalmente, possibilitando que as pessoas desçam. Qual é aceleração da roda gigante?

a) – 5 m/s²

b) 5 m/s²

c) – 0, 9 m/s²

d) 0,06 m/s²

e) – 0,025m/s²

Ver resposta

Resposta

Letra E

d = 100 m
ω₀ = 0,02 rad/s
ω = 0 rad/s
t = 40 s
a = ?

$\omega=\omega_0+\alpha·t$

$0=0,02+\alpha·40$

$-\alpha·40=0,02$

$\alpha=\frac{0,02}{-40}=-0,0005\ rad/s^2$

Se d = 100, o raio é a metade disso.

$a=\alpha·R=-0,0005·50=-0,025\ m/s²$

O valor obtido foi negativo já que a roda gigante terá sua velocidade reduzida com o tempo.

Questão 10

Duas engrenagens de uma mesma máquina se movem ao mesmo tempo e com a mesma velocidade linear em um determinado momento t. A engrenagem P possui raio igual a 10 cm, e a engrenagem Q possui diâmetro igual a 16 cm. Ambas possuem exatamente a mesma aceleração angular. Analise as afirmações a seguir em relação ao que ocorrerá após o tempo t.

a) A velocidade angular de P será maior que a de Q, porque seu raio é menor.

b) A velocidade angular de P será maior que a de Q, porque seu raio é maior.

c) A aceleração de P será maior que a de Q, porque seu raio é maior.

d) A aceleração de Q será maior que a de P, porque seu raio é maior.

Ver resposta

Resposta

Letra C

Quanto maior o raio de um percurso, quando se tem grandezas lineares iguais, menores as grandezas angulares, sendo inversamente proporcionais. Em contrapartida, quando se tem grandezas angulares iguais, quanto maior o raio, maiores as grandezas lineares, sendo diretamente proporcionais.

Grandezas angulares	Grandezas lineares
$∆θ=\frac{∆S}R$	$∆S=∆θ·R$
$\omega=\frac{v}{R}$	$v=\omega·R$
$\alpha=\frac{a}{R}$	$a=\alpha·R$

Questão 11

Um motor de rotação, acoplado a uma broca com ponta de diamante de uma mineradora, é utilizado para perfurar rochas grandes com um alto índice de dureza. Sua aceleração é aproximadamente igual a 15 rad/s² desde o momento em que o motor é ligado. Sendo assim, qual o deslocamento angular necessário para sua velocidade de rotação ser igual a 600 rad/s?

a) 500 rad

b) 1200 rad

c) 600 rad

d) 2000 rad

e) 100 rad

Ver resposta

Resposta

Letra B

ω₀ = 0
ω = 600 rad/s
α = 15 rad/s²
Δθ = ?

$\omega^2=\omega_0^2+2·α·∆θ$

${600}^2=0²+2·15·∆θ$

$360000=30·∆θ$

$30.∆θ=360000$

$∆θ=\frac{360000}30=12000\ rad$

Questão 12

Em uma apresentação circense, um trapezista utilizou uma corda de 12 metros de comprimento para se mover de um lado a outro do picadeiro, descrevendo assim um terço de uma circunferência. Sua aceleração angular foi de 8 rad/s² na descida, logo sua velocidade angular no ponto mais baixo do trajeto foi de:

Utilize π = 3.

a) 9 rad/s

b) 11 rad/s

c) 15 rad/s

d) 4 rad/s

e) 21 rad/s

Ver resposta

Resposta

Letra D

R = 12 m
α = 8 rad/s²
ω = ?

O trajeto equivale a um terço de uma circunferência. Porém, em uma metade do trajeto ele desceu e na outra metade ele subiu, logo a velocidade desejada é a máxima, a que ele obteve no final da descida. Primeiramente, deve-se calcular o deslocamento angular. Para isso, é necessário o comprimento percorrido. Se o trajeto todo possui 1/3 da circunferência, metade disso seria 1/6. Sendo assim, deve-se calcular o comprimento de 1/6 dessa circunferência.

$∆S=\frac{2·π·R}6=\frac{2·3·12}6=\frac{72}6=12\ m$