Exercícios sobre ondas periódicas
Esta lista de exercícios testará seus conhecimentos sobre os principais elementos das ondas periódicas, a saber: equação, período, frequência, amplitude e comprimento de onda.
Publicado por: Rafael HelerbrockQuestões
-
Questão 1
(Ufes) A velocidade de uma onda sonora no ar é 340 m/s, e seu comprimento de onda é 0,340 m. Passando para outro meio, onde a velocidade do som é o dobro (680 m/s), os valores da frequência e do comprimento de onda no novo meio serão, respectivamente:
a) 400 Hz e 0,340 m
b) 500 Hz e 0,340 m
c) 1000 Hz e 0,680 m
d) 1200 Hz e 0,680 m
e) 1360 Hz 1,360 m
Letra C
A equação das ondas que relaciona velocidade de propagação, comprimento de onda e frequência é a seguinte:
.gif)
De acordo com os dados do exercício, a velocidade de propagação da onda no primeiro meio é de 340 m/s, e seu comprimento de onda é de 0,340 m, logo:
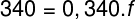
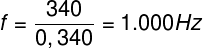
A frequência de oscilação de onda não muda com a refração e depende somente da fonte das ondas. O comprimento de onda dessa oscilação pode ser calculado pela mesma equação utilizada anteriormente, mas com o novo valor de velocidade da onda:
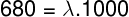
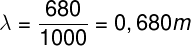
Dessa forma:
λ = 0,680 m e f = 1000 Hz
-
Questão 2
(Ufac) - A velocidade do som no ar, a determinada temperatura, é de 340 m/s. Em média, o ouvido humano é capaz de ouvir sons entre 20 Hz e 20.000 Hz. Sendo assim, o som mais agudo (maior frequência) que o ouvido humano possui a capacidade de ouvir tem comprimento de onda igual a:
a) 20 cm
b) 20.000 cm
c) 17 mm
d) 17 cm
e) 17 dm
Letra C
Usamos a equação da dispersão da onda:
.gif)
Usando os valores fornecidos pelo enunciado, temos que:
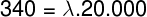
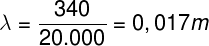
Se expressarmos o resultado obtido anteriormente na base decimal, perceberemos que:
0,017m = 17.10-3 m = 17 mm
-
Questão 3
Determinada onda apresenta uma distância de 20 cm entre suas cristas e período de 0,5 s. Assinale a alternativa que apresente corretamente sua frequência, velocidade de propagação e frequência angular, respectivamente.
a) 0,5 Hz; 0,10 m/s; 2 rad/s
b) 1 Hz; 1 m/s; 2 rad/s
c) 0,5 Hz; 0,10 m/s; 2π rad/s
d) 2 Hz; 0,40 m/s; 4π rad/s
e) 1 Hz; 0,10 m/s; π rad/s
Letra D
A relação entre período e frequência é dada por:
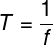
Atribuindo os valores presentes no enunciado, temos:
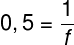
Agora vamos fazer a multiplicação cruzada dos termos:
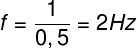
Encontramos assim a frequência de oscilação de 2 Hz. Em seguida, devemos utilizar a relação de dispersão das ondas para calcular sua velocidade de propagação:
.gif)
Atribuindo os valores informados pelo enunciado do exercício, temos:
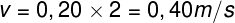
Logo, a velocidade de propagação dessa onda é de 0,40 m/s. Para calcular a frequência angular, utilizamos a seguinte relação:
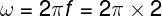
Encontramos, portanto, a frequência angular de 4π rad/s.
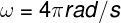
-
Questão 4
Uma função de onda é expressa pela equação:
.gif)
Assinale a alternativa que apresente valores corretos de amplitude, período, comprimento de onda e velocidade de propagação, respectivamente.
a) 8 m, 2 s; 4 m; 2 m/s;
b) 8 m, 4 s; 2 m; 8 m/s;
c) 8 m, 4 s; 2 m; 4 m/s;
d) 8 m, 4 s; 2 m; 1 m/s;
e) 4 m, 8 s; 8 m; 2 m/s;
Letra A
A forma geral da equação das ondas periódicas é dada por:
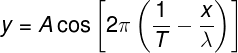
Podemos identificar apenas observando o formato da equação fornecida no enunciado que:
-
A amplitude de oscilação da onda (A) é de 8 m;
-
Seu período (T) é de 2 s;
-
Seu comprimento de onda (λ) é de 4 m.
Para calcular a velocidade de propagação da onda, utilizamos a equação:
.gif)
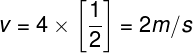
-
