Exercícios sobre primeira lei de Ohm
Qual alternativa abaixo corresponde à fórmula da primeira lei de Ohm?
A) \( i=\frac{P_{OT}}{U}\)
B) \(U=\sqrt{P_{OT}\cdot R}\)
C) \(R=\frac{U^2}{P_{OT}}\)
D) \(R=\frac{P_{OT}}{i^2}\)
E) \(U=R\cdot i\)
Alternativa E
A fórmula da primeira lei de Ohm é \(R=\frac{U}{i}\) , que também é representada por \(U=R\cdot i\).
Qual(is) das alternativa(s) apresenta(m) a unidade de medida correspondente à grandeza física estudada na primeira lei de Ohm?
I. A diferença de potencial é medida em Ohm.
II. A resistência elétrica é medida em Ampere.
III. A corrente elétrica é medida em Volts.
A) Apenas I.
B) Alternativas II e III
C) Alternativas I e III.
D) Todas as alternativas estão incorretas.
E) Todas as alternativas estão corretas.
Alternativa D
I. A diferença de potencial é medida em Ohm. (falso)
A diferença de potencial é medida em Volts.
II. A resistência elétrica é medida em Ampere. (falso)
A resistência elétrica é medida em Ohm.
III. A corrente elétrica é medida em Volts. (falso)
A corrente elétrica é medida em Ampere.
Um aparelho possui um resistor com determinada resistência elétrica. Ele é inserido em uma tomada de 110 V , sendo percorrido por uma corrente elétrica de 4 μA . Então, determine a resistência elétrica desse resistor.
A) 27,5 ∙ 10-4 Ω
B) 27,5 ∙ 10-5 Ω
C) 27,5 ∙ 10-6 Ω
D) 27,5 ∙ 10-7 Ω
E) 27,5 ∙ 10-8 Ω
Alternativa C
Calcularemos o valor da resistência elétrica por meio da fórmula da primeira lei de Ohm:
\(R=\frac{U}{i}\)
\(R=\frac{110}{4\ \mu}\)
O símbolo μ representa 10-6 , portanto:
\(R=\frac{110}{4\cdot{10}^{-6}}\)
\(R=27,5\cdot{10}^{-6}\ \Omega\)
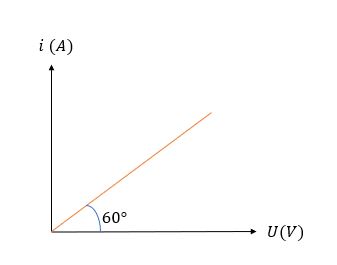
Determine o valor da resistência elétrica de acordo com as informações dadas no gráfico abaixo.
Qual alternativa apresenta a resposta correta?
A) 0,866 Ω
B) 0,577 Ω
C) 1 Ω
D) 1,73 Ω
E) Não é possível calcular.
Alternativa D
Podemos calcular a resistência elétrica por meio da primeira lei de Ohm, mas como nos foi dado apenas o ângulo entre a corrente e a tensão, usaremos a fórmula que envolve a tangente desse ângulo:
\(R=\tan{\theta}\)
\(R=tan60°\)
\(R=\sqrt3\ \Omega\)
\(R\approx1,73\ \Omega\)
Um resistor de 9∙10-8Ω é percorrido por uma corrente elétrica com valor de 25 A . A tensão elétrica entre os terminais do resistor é:
A) 2,25 MV
B) 2,25 μV
C) 2,25 nV
D) 2,25 mV
E) 2,25 pV
Alternativa B
Calcularemos o valor da tensão elétrica usando a primeira lei de Ohm:
U=R∙i
U = 9 ∙10-8 ∙ 25
U = 225 ∙10-8
U = 2,25 ∙102∙10-8
U = 2,25 ∙102-8
U = 2,25 ∙10-6
Sendo que 10-6 é representado por micro, que pode ser representado por:
U=2,25 μV
Conectando um resistor em uma tomada de 240 V, ele será percorrido por uma corrente elétrica de 10 A . Então, com as informações dadas, determine o valor da resistência elétrica desse resistor.
A) 24 Ω
B) 2,4 Ω
C) 2,44 Ω
D) 0,24 Ω
E) 0,024 Ω
Alternativa A
Determinaremos o valor da resistência por meio da primeira lei de Ohm:
\(R=\frac{U}{i}\)
\(R=\frac{240}{10}\)
\(R=24\ \Omega\)
Determine a corrente elétrica em um resistor de 50 mΩ inserido em uma ddp de 110 V.
A) 2,2 ∙102 A
B) 2,2 ∙10-4 A
C) 2,2 ∙104 A
D) 2,2 ∙10-3 A
E) 2,2 ∙103 A
Alternativa E
Encontraremos o valor da corrente por meio da primeira lei de Ohm:
\(U=R\cdot i\)
\(110=50m\cdot i\)
Sendo que o m de 50 mΩ é o mili, cujo valor é 10-3 :
\(110=50\cdot{10}^{-3}\cdot i\)
\(i=\frac{110}{50\cdot{10}^{-3}}\)
\(i=2,2\cdot{10}^3\ A\)
Dois resistores estão associados em série com resistências iguais ao valor de 10 Ω. Sabendo que são atravessados por uma corrente de 11 A, determine a ddp entre eles.
A) 220 V
B) 55 V
C) 110 V
D) 50 V
E) 400 V
Alternativa A
Primeiramente, precisamos encontrar a resistência equivalente na associação de resistores em série, em que basta somarmos as resistências:
\(R_{eq}=R_1+R_2\)
\(R_{eq}=10+10\)
\(R_{eq}=20\ \Omega\)
Agora, podemos calcular a ddp nesse circuito, utilizando a fórmula da primeira lei de Ohm:
\(U=20\cdot11\)
\(U=220\ V\)
(Uneb-BA) Um resistor ôhmico, quando submetido a uma ddp de 40 V, é atravessado por uma corrente elétrica de intensidade 20 A. Quando a corrente que o atravessa for igual a 4 A, a ddp, em volts, nos seus terminais, será:
A) 8
B) 12
C) 16
D) 20
E) 30
Alternativa A
Primeiramente, vamos determinar a resistência do resistor, por meio da fórmula da primeira lei de Ohm:
\(R=\frac{U}{i}\)
\(R=\frac{40}{20}\)
\(R=2\ \Omega\)
Encontraremos o valor da ddp quando esse resistor é atravessado por uma nova corrente de 4 A, utilizando outra representação da fórmula da primeira lei de Ohm:
\(U=R\cdot i\)
\(U=2\cdot4\)
\(U=8\ V\)
(UCSal-BA) Um resistor de 100 Ω é percorrido por uma corrente elétrica de 20 mA. A ddp entre os terminais do resistor, em volts, é igual a:
A) 2,0
B) 5,0
C) 2,0∙10
D) 2,0 ∙103
E) 5,0 ∙103
Alternativa A
Calcularemos a ddp entre os terminais usando a fórmula da primeira lei de Ohm:
\(U=R\cdot i\)
\(U=100\cdot20m\)
Sendo que o m de 20 mΩ é o mili, cujo valor é 10-3 :
\(U=100\cdot20\cdot{10}^{-3}\)
\(U=2000\cdot{10}^{-3}\)
\(U=2\cdot{10}^3\cdot{10}^{-3}\)
\(U=2\cdot{10}^{3-3}\)
\(U=2\cdot{10}^0\)
\(U=2\cdot1\)
\(U=2\ V\)
(UFC-CE) Um pássaro pousa em um dos fios de uma linha de transmissão de energia elétrica. O fio conduz uma corrente elétrica i = 1.000 A, e sua resistência, por unidade de comprimento, é de 5,0 ∙ 10-5 Ω/m. A distância que separa os pés do pássaro, ao longo do fio, é de 6,0 cm. A diferença de potencial, em milivolts (mV), entre os seus pés é:
A) 1,0
B) 2,0
C) 3,0
D) 4,0
E) 5,0
Alternativa C
Primeiramente, encontraremos o valor da resistência elétrica na distância que separa os pés do passarinho. Já que a resistência foi dada em função do comprimento do fio, basta multiplicarmos seu valor pelo comprimento:
\(R=R_{por\ comprimento}\cdot L\)
Convertendo a distância entre os pés do passarinho de centímetro para metros, em que 6 cm = 0,06 m, então:
\(R=5,0\cdot{10}^{-5}\cdot0,06\)
\(R=0,3\cdot{10}^{-5}\ \Omega\)
Por fim, para calcularmos a tensão elétrica, basta utilizarmos a primeira lei de Ohm:
\(U=R\cdot i\)
\(U=0,3\cdot{10}^{-5}\cdot1000\)
\(U=300\cdot{10}^{-5}\)
\(U=3\cdot{10}^2\cdot{10}^{-5}\)
\(U=3\cdot{10}^{2-5}\)
\(U=3\cdot{10}^{-3\ }V\)
\(U=3\ mV\)
(UEL) Um resistor de 10 Ω no qual flui uma corrente elétrica de 3,0 Amperes está associado em paralelo com outro resistor. Sendo a corrente elétrica total, na associação, igual a 4,5 Amperes, o valor do segundo resistor, em Ohms, é:
A) 5,0
B) 10
C) 20
D) 30
E) 60
Alternativa C
Primeiramente, vamos calcular a ddp no resistor de 10 Ω percorrido pela corrente de 3 A, utilizando a primeira lei de Ohm:
\(U=R\cdot i\)
\(U=10\cdot3\)
\(U=30\ V\)
Como o segundo resistor está em paralelo com o primeiro, sabemos que a ddp será igual para ambos, então a resistência do segundo resistor é:
\(R=\frac{U}{i}\)
A corrente do segundo resistor será a corrente total menos a corrente do primeiro resistor:
\(R=\frac{30}{(4,5-3)}\)
\(R=\frac{30}{1,5}\)
\(R=20\ \Omega\)
