Exercícios sobre segunda lei de Newton
(Afasp) Durante um intervalo de tempo de 4 s, atua uma força constante sobre um corpo de massa 8,0 kg que está inicialmente em movimento retilíneo com velocidade escalar de 9 m/s. Sabendo-se que no fim desse intervalo de tempo a velocidade do corpo tem módulo de 6 m/s, na direção e sentido do movimento original, a força que atuou sobre ele tem intensidade de:
A) 3,0 N no sentido do movimento original.
B) 6,0 N em sentido contrário ao movimento original.
C) 12,0 N no sentido do movimento original.
D) 24,0 N em sentido contrário ao movimento original.
Alternativa B
Primeiramente, vamos calcular a aceleração do corpo por meio da fórmula que a relaciona a velocidade e ao tempo:
\(v=v_o±a\cdot t\)
Como houve uma desaceleração, a aceleração é negativa:
\(6=9-a\cdot4\)
\(6-9=-a\cdot4\)
\(-3=-a\cdot4\)
\(3=a\cdot4\)
\(a=\frac{3}4\)
\(a=0,75 m/s^2 \)
Então, encontraremos a intensidade da força usando a segunda lei de Newton:
\(F_R=m\cdot a\)
\(F_R=8\cdot0,75\)
\(F_R=6\ N\)
A força está no sentido contrário do movimento inicial, já que a velocidade do corpo diminuiu.
(Enem) Para um salto no Grand Canyon usando motos, dois paraquedistas vão utilizar uma moto cada, sendo que uma delas possui massa três vezes maior. Foram construídas duas pistas idênticas até a beira do precipício de forma que no momento do salto as motos deixem a pista horizontalmente e ao mesmo tempo. No instante em que saltam, os paraquedistas abandonam suas motos e elas caem praticamente sem resistência do ar. As motos atingem o solo simultaneamente porque
A) possuem a mesma inércia.
B) estão sujeitas à mesma força resultante.
C) têm a mesma quantidade de movimento inicial.
D) adquirem a mesma aceleração durante a queda.
E) são lançadas com a mesma velocidade horizontal.
Alternativa D
Como foi desconsiderada a resistência do ar, a massa não vai interferir no tempo de queda. Eles saltaram da mesma altura, então a aceleração que atuará sobre eles é a aceleração da gravidade, que é a mesma para todos os corpos em uma mesma altura. Assim, as motos chegarão ao solo simultaneamente, porque adquirem a mesma aceleração durante a queda.
(Fuvest) Um veículo de 5 kg descreve uma trajetória retilínea que obedece à seguinte equação horária: \(s=3t^2+2t+1\), em que s é medido em metros e t, em segundos. O módulo da força resultante sobre o veículo vale:
A) 30 N
B) 5 N
C) 10 N
D) 15 N
E) 20 N
Alternativa A
Essa equação horária é similar a uma das fórmulas do movimento uniformemente variado:
\(s=s_o+v_o\cdot t+\frac{at^2}2\)
Reorganizando a equação horária, conseguimos identificar os termos correspondentes:
\(s=1+2t+3t^2\)
Assim:
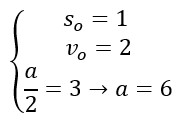
Portanto, a força resultante pode ser calculada pela fórmula da segunda lei de Newton:
\(F_R=m\cdot a\)
\(F_R=5\cdot6\)
\(F_R=30\ N\)
(UFMG) Um corpo de massa m está sujeito à ação de uma força F que o desloca segundo um eixo vertical em sentido contrário ao da gravidade. Se esse corpo se move com velocidade constante, é porque:
A) a força F é maior do que a da gravidade.
B) a força resultante sobre o corpo é nula.
C) a força F é menor do que a gravidade.
D) a diferença entre os módulos das duas forças é diferente de zero.
E) a afirmação da questão está errada, pois qualquer que seja F o corpo estará acelerado porque sempre existe a aceleração da gravidade.
Alternativa B
Como o corpo se move a uma velocidade constante, isso significa que sua aceleração é nula, então a sua força resultante também será nula.
Um objeto de 500 gramas está sobre uma superfície horizontal, sujeito à ação da força peso. Determine o módulo da força peso sobre esse objeto, sabendo que a aceleração da gravidade é de aproximadamente \(9,8\ m/s^2 \).
A) 4900 N
B) 2450 N
C) 245 N
D) 490 N
E) 4,9 N
Alternativa E
Inicialmente, converteremos a massa de gramas em quilogramas:
\(500\ g=0,5\ kg\)
Por fim, vamos calcular o módulo da força peso por meio da sua fórmula:
\(P=m\cdot g\)
\(P=0,5\cdot9,8\)
\(P=4,9\ N\)
Qual a aceleração adquirida por um carro de 900 kg que é empurrado por duas pessoas que fazem uma força resultante de 13 500 N?
A) \(14\ m/s^2 \)
B) \(20\ m/s^2 \)
C) \(15\ m/s^2 \)
D) \(12\ m/s^2 \)
E) \(17\ m/s^2 \)
Alternativa C
Calcularemos a aceleração do carro usando a fórmula da segunda lei de Newton:
\(F_R=m\cdot a\)
\(13500=900\cdot a\)
\(a=\frac{13500}{900}\)
\(a=15\ m/s^2 \)
Qual a massa de um bloco puxado por um carro com força de 1500 N que adquire aceleração de \(10\ m/s^2 \)?
A) 1500 kg
B) 15 kg
C) 1,5 kg
D) 150 kg
E) 0,15 kg
Alternativa D
Descobriremos a massa do bloco por meio da fórmula da segunda lei de Newton:
\(F_R=m\cdot a\)
\(1500=m\cdot10\)
\(m=\frac{1500}{10}\)
\(m=150\ kg\)
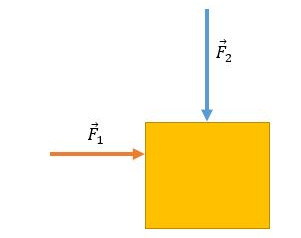
Duas pessoas empurram uma caixa da forma que vemos na imagem a seguir. Sabendo que a força que a primeira pessoa faz é \(\vec{F}_1\) e a força que a segunda pessoa faz é \(\vec{F}_2\), cujos valores são \(\vec{F}_1\) =30 N e \(\vec{F}_2\) =40 N, encontre o módulo da força resultante que move a caixa.
A) 50 N
B) 40 N
C) 30 N
D) 20 N
E) 10 N
Alternativa A
Podemos perceber que as forças na caixa são perpendiculares, portanto para calcular a força resultante usaremos o teorema de Pitágoras:
\(\vec{F_R}^2=\vec{F_1}^2+\vec{F_2}^2\)
\(\vec{F_R}^2=30^2+40^2\)
\(\vec{F_R}^2=900+1600\)
\(\vec{F_R}^2=2500\)
\(\vec{F_R}=\sqrt{2500}\)
\(\vec{F_R}=50\ N\)
Uma família está fazendo sua mudança e precisou mover uma caixa de massa 40 kg para dentro do caminhão. Ela foi movida por seus dois filhos simultaneamente, sendo que o primeiro aplicou uma força de 60 N e o segundo aplicou uma força de 20 N. Assim, encontre o valor da força resultante e a aceleração da caixa.
A) \(1\ m/s^2 \)
B) \(2\ m/s^2 \)
C) \(3\ m/s^2 \)
D) \(4\ m/s^2 \)
E) \(5\ m/s^2 \)
Alternativa B
Como os irmãos movem a caixa simultaneamente no mesmo sentido, a força resultante é a soma de suas forças:
\(\vec{F_R}=\vec{F_1}+\vec{F_2}\)
\(\vec{F_R}=60+20\)
\(\vec{F_R}=80\ N\)
Para encontrarmos a aceleração dessa caixa, basta usarmos a fórmula da segunda lei de Newton:
\(\vec{F_R}=m\cdot \vec{a}\)
\(80=40\cdot \vec{a}\)
\(\vec{a}=\frac{80}{40}\)
\(\vec{a}=2\ m/s^2 \)
Algumas crianças brincam de cabo de guerra. Do lado esquerdo, há três crianças fazendo as forças \(\vec{F_1}=10\ N\), \(\vec{F_2}=15\ N\) e \(\vec{F_3}=30\ N\). Já do lado direito há outras três crianças, que fazem as forças \(\vec{F_4}=40\ N\), \(\vec{F_5}=15\ N\) e \(\vec{F_6}=5\ N\). Determine o módulo da força resultante na corda e qual dos lados ganhará a brincadeira.
A) \(-5\ N\), lado direito.
B) \(-5\ N\), lado esquerdo.
C) 5 N, lado direito.
D) 0 N, nenhum lado.
E) 5 N, lado esquerdo.
Alternativa E
Como as crianças fazem força em sentidos opostos, para encontrarmos a força resultante é necessário subtrair as forças do lado esquerdo com as forças do lado direito:
\(\vec{F_R}=\vec{F_1}+\vec{F_2}+\vec{F_3}-(\vec{F_4}+\vec{F_5}+\vec{F_6})\)
\(\vec{F_R}=10+15+30-(40+15+5)\)
\(\vec{F_R}=55-(60)\)
\(\vec{F_R}=55-60\)
\(\vec{F_R}=-5\ N\)
O módulo da força resultante é sempre positivo, portanto esse sinal negativo indica que o lado ganhador é o lado direito, que fez mais força que o lado esquerdo.
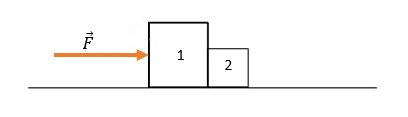
Uma força F é aplicada sobre dois blocos, de massa \(m_1=10\ kg\) e \(m_2=5\ kg\), que adquirem uma aceleração de \(4\ m/s^2 \), conforme podemos verificar na imagem a seguir. Em vista disso, encontre o valor da força F.
A) 70 N
B) 40 N
C) 60 N
D) 20 N
E) 30 N
Alternativa C
Determinaremos a força resultante por meio da fórmula da segunda lei de Newton:
\(\vec{F_R}=m\cdot \vec{a}\)
Como os blocos estão em contato, a massa será a soma da massa de cada bloco:
\(F_R=(10+5)\cdot4\)
\(F_R=(15)\cdot4\)
\(F_R=60\ N\)
Quais das alternativas apresentam a unidade de medida correspondente à grandeza física estudada na segunda lei de Newton?
I. A força peso é medida em metros por segundo ao quadrado.
II. A força resultante é medida em Newton.
III. A velocidade é medida em metros por segundo.
IV. A aceleração é medida em Newton.
V. A massa é medida em Coulomb por metro.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Nenhuma das alternativas está correta.
Alternativa D
I. A força peso é medida em metros por segundo ao quadrado. (Falso)
A força peso é medida em Newton.
II. A força resultante é medida em Newton. (Verdadeiro)
III. A velocidade é medida em metros por segundo. (Verdadeiro)
IV. A aceleração é medida em Newton. (Falso)
A aceleração é medida em metros por segundo ao quadrado.
V. A massa é medida em Coulomb por metro. (Falso)
A massa é medida em quilogramas.
