Enem: lista de exercícios sobre equação e função polinomial do 2º grau
Com esta lista de exercícios, você testa seus conhecimentos sobre equação e função polinomial do segundo grau e se prepara para a prova de Matemática do Enem.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(IFSC 2017) Pedro é pecuarista e, com o aumento da criação, ele terá que fazer um novo cercado para acomodar seus animais. Sabendo-se que ele terá que utilizar 5 voltas de arame farpado e que o cercado tem forma retangular cujas dimensões são as raízes da equação x² − 45x+500=0, qual a quantidade mínima de arame que Pedro terá que comprar para fazer esse cercado.
A) 545 m.
B) 225 m.
C) 200 m.
D) 500 m.
E) 450 m.
Alternativa E.
Queremos encontrar as raízes da equação. Para isso, calcularemos o valor do delta e aplicaremos a fórmula de Bhaskara:
x² − 45x+500=0
- a= 1
- b = – 45
- c = 500
Calculando o delta:
Δ = b² – 4ac
Δ = ( – 45)² – 4·1·500
Δ = 2025 – 2000
Δ = 25
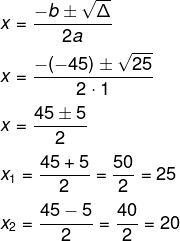
Sabendo que as dimensões são 20 m e 25 m, então o perímetro é de:
P = 2 ∙ 20 + 2 ∙ 25 = 40 + 50 = 90
Como serão 5 voltas, então a quantidade necessária será de:
5 ∙ 90 = 450 m
-
Questão 2
(Enem 2016) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = −2t²+ 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.
A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1 600 pessoas, e uma segunda dedetização precisou acontecer.
A segunda dedetização começou no:
A) 19º dia.
B) 20º dia.
C) 29º dia.
D) 30º dia.
E) 60º dia.
Alternativa B.
Queremos o valor de t para que – 2t² + 120t = 1600.
Arrumando a equação do 2º grau, temos que:
– 2t² + 120t – 1600 = 0
a = – 2; b = 120 e c = – 1600
∆ = (-120)² – 4.2.160
∆ = 14400 – 12800
∆ = 1600
Agora aplicando a fórmula de Bhaskara:
\(t=\frac{-b\pm\sqrt\Delta}{2a}\)
\(t=\frac{-b\pm\sqrt\Delta}{2a}\)
\(t=\frac{-120\pm\sqrt{1600}}{2\cdot\left(-2\right)}\)
\(t=\frac{-120\pm40}{-4}\)
\(t_1=\frac{-120+40}{-4}=\frac{-80}{-4}=20\)
\(t_2=\frac{-120-40}{-4}=\frac{-160}{-4}=40\)
Logo, a segunda dedetização começou no 20º dia.
-
Questão 3
(Enem 2015) Um estudante está pesquisando o desenvolvimento de certo tipo de bactéria. Para essa pesquisa, ele utiliza uma estufa para armazenar as bactérias. A temperatura no interior dessa estufa, em graus Celsius, é dada pela expressão T(h) = –h² + 22h – 85, em que h representa as horas do dia. Sabe-se que o número de bactérias é o maior possível quando a estufa atinge sua temperatura máxima e, nesse momento, ele deve retirá-las da estufa. A tabela associa intervalos de temperatura, em graus Celsius, com as classificações: muito baixa, baixa, média, alta e muito alta.
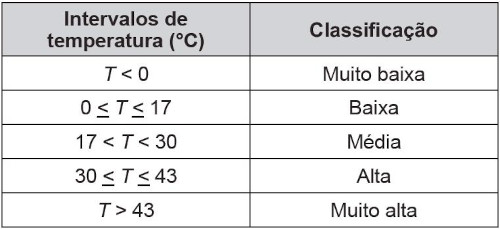
Quando o estudante obtém o maior número possível de bactérias, a temperatura no interior da estufa está classificada como:
A) muito baixa.
B) baixa.
C) média.
D) alta.
E) muito alta.
Alternativa D.
Calcularemos o valor do yv da função e, para isso, é necessário encontrar o valor de Δ também.
Na função T(h) = –h2 + 22h – 85, temos que: a = – 1; b = 22; e c = – 85.
Calculando Δ:
Δ = b2 – 4ac
Δ = 22² – 4 ( – 1) ( – 85)
Δ = 484 – 340
Δ = 144
Então calculando yv, temos que:
\(y_v = \frac{-\Delta}{4\cdot a}\)
\(y_v = \frac{-144}{4\cdot (-1)}\)
\(y_v = \frac{-144}{-4}\)
\(y_v = 36\)
Se T = 36, sabemos que ele está entre 30 e 40. Essa temperatura é classificada como alta.
-
Questão 4
(Enem 2015) Um meio de transporte coletivo que vem ganhando espaço no Brasil é a van, pois realiza, com relativo conforto e preço acessível, quase todos os tipos de transportes: escolar e urbano, intermunicipal e excursões em geral.
O dono de uma van, cuja capacidade máxima é de 15 passageiros, cobra para uma excursão até a capital de seu estado R$ 60,00 de cada passageiro. Se não atingir a capacidade máxima da van, cada passageiro pagará mais R$ 2,00 por lugar vago.
Sendo x o número de lugares vagos, a expressão que representa o valor arrecadado V(x), em reais, pelo dono da van, para uma viagem até a capital é:
A) V(x) = 902x
B) V(x) = 930x
C) V(x) = 900 + 30x
D) V(x) = 60x + 2x²
E) V(x) = 900 – 30x – 2x²
Alternativa E.
Seja x o número de pessoas que não compareceram. O pagamento pelo lugar ocupado é calculado por 60 · ( 15 – x). Além disso, cada um pagará 2 reais por vaga não ocupada, ou seja, 2x ( 15 – x), então:
V(x) = 60 ( 15 – x) + 2x ( 15 – x)
V(x) = 900 – 60x + 30x – 2x²
V(x) = 900 – 30x – 2x²
-
Questão 5
(Enem 2017 | Libras) A única fonte de renda de um cabeleireiro é proveniente de seu salão. Ele cobra R$ 10,00 por cada serviço realizado e atende 200 clientes por mês, mas está pensando em aumentar o valor cobrado pelo serviço. Ele sabe que cada real cobrado a mais acarreta uma diminuição de 10 clientes por mês.
Para que a renda do cabeleireiro seja máxima, ele deve cobrar por serviço o valor de:
A) R$ 10,00.
B) R$ 10,50.
C) R$ 11,00.
D) R$ 15,00.
E) R$ 20,00.
Alternativa D.
Seja x o valor do aumento em reais e R(x). Sabemos que 200 – 10x é igual ao número de clientes após o aumento de x reais e que 10 + x é o valor do serviço após o aumento, então:
R(x) = (200 – 10x) (10 + x)
R(x) = 2000 + 200x – 100x – 10x²
R(x) = – 10x² + 100x + 200
Queremos o valor máximo que ele pode alcançar. Calcularemos o valor de xv:
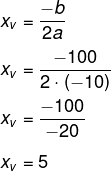
Com o aumento de 5 reais, o valor do serviço chega a R$ 15,00.
-
Questão 6
(Enem 2017) Viveiros de lagostas são construídos, por cooperativas locais de pescadores, em formato de prismas reto-retangulares, fixados ao solo e com telas flexíveis de mesma altura, capazes de suportar a corrosão marinha. Para cada viveiro a ser construído, a cooperativa utiliza integralmente 100 metros lineares dessa tela, que é usada apenas nas laterais.
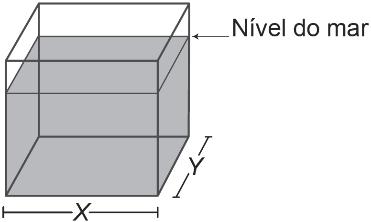
Quais devem ser os valores de X e de Y, em metro, para que a área da base do viveiro seja máxima?
A) 1 e 49.
B) 1 e 99.
C) 10 e 10.
D) 25 e 25..
E) 50 e 50.
Alternativa D.
Sabemos que o perímetro é igual a 100, logo temos que:
2X + 2Y = 100 → dividindo toda a equação por 2
X + Y = 50
Y = 50 – X
Por outro lado, a área é dada por X · Y, então temos que:
A = X (50 – X)
A = – X² + 50X
a = – 1 b = 50 e c = 0
Calculando o X do vértice, temos que:
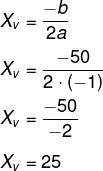
Então, a melhor medida para X e Y é ambos medindo 25 m.
-
Questão 7
(UEL) A função real f, de variável real, dada por f(x) = – x² + 12x + 20, tem um valor:
A) mínimo, igual a -16, para x = 6.
B) mínimo, igual a 16, para x = -12.
C) máximo, igual a 56, para x = 6.
D) máximo, igual a 72, para x = 12.
Alternativa C.
Como a = – 1, o gráfico da parábola terá concavidade para baixo, logo o vértice será o máximo da função. Então, para encontrar o vértice, temos que: a = – 1, b = 12 e c = 20.
Δ = b² – 4ac
Δ = 12² – 4 · ( – 1) · 20
Δ = 144 + 80
Δ = 224
Agora calcularemos yv e xv:
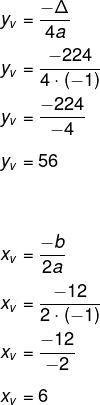
Então, podemos afirmar que o valor máximo da função é igual a 56, para x = 6.
-
Questão 8
(Enem 2017 | Libras) O morro onde estão situadas as emissoras de TV em Porto Alegre pode ser representado graficamente, com algum prejuízo, em um sistema cartesiano, através de uma função polinomial de grau 2 da forma y = ax² + bx + c, com a base da montanha no eixo das abscissas.

Para que fique mais adequado essa representação, devemos ter:
A) a > 0 e b² – 4ac > 0
B) a > 0 e b² – 4ac < 0
C) a < 0 e b² – 4ac < 0
D) a < 0 e b² – 4ac > 0
E) a < 0 e b² – 4ac = 0
Alternativa D.
Analisando o gráfico, sabemos que essa parábola tem concavidade para baixo, logo a < 0. Sabemos também que b² – 4ac = Δ.
Como a base da montanha é o eixo das abscissas, a parábola toca em dois pontos essa base, logo:
b² – 4ac > 0
Então, a < 0 e b² – 4ac > 0.
-
Questão 9
(Enem 2013) Uma pequena fábrica vende seus bonés em pacotes com quantidades de unidades variáveis. O lucro obtido é dado pela expressão L(x) = – x² + 12x – 20, onde x representa a quantidade de bonés contidos no pacote. A empresa pretende fazer um único tipo de empacotamento, obtendo um lucro máximo.
Para obter o lucro máximo nas vendas, os pacotes devem conter uma quantidade de bonés igual a:
A) 4.
B) 6 .
C) 9.
D) 10.
E) 14.
Alternativa B.
A quantidade de bonés para maximizar o lucro é igual ao xv.
Na função, temos que:
-
a = – 1
-
b = 12
-
c = – 20
Logo:
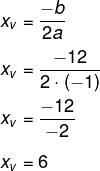
-
-
Questão 10
(Enem 2013) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão:
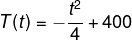
com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39 ºC.
Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
A)19,0
B)19,8
C) 20,0
D) 38,0
E) 39,0
Alternativa D.
Queremos que T(t) = 39.
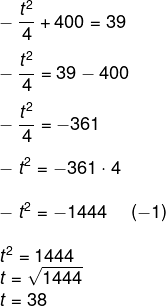
-
Questão 11
(Enem 2017) A Igreja de São Francisco de Assis, obra arquitetônica modernista de Oscar Niemeyer, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólica. A seta na Figura 1 ilustra uma das abóbadas na entrada principal da capela. A Figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos.
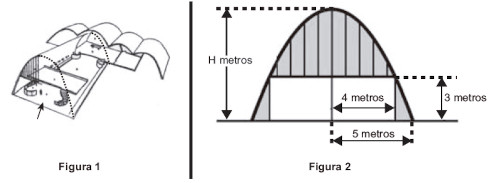
Qual a medida da altura H, em metro, indicada na Figura 2?
A) 16/3
B) 31/5
C) 24/4
D) 25/3
E) 75/2
Alternativa D.
Como as raízes da equação são 5 e – 5, então a equação da parábola é dada por:
f(x) = a(x – 5)(x+5)
f(x) = a(x² – 25)
Sabemos que o ponto (4,3) pertence a essa equação, então temos que:
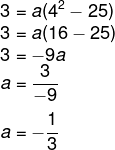
Desse modo, a lei de formação da função será:
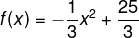
Agora, para calcular o valor do yv, primeiro encontraremos o valor de delta e, posteriormente, o valor de yv:
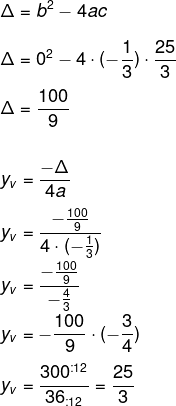
-
Questão 12
(Enem 2013) A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.
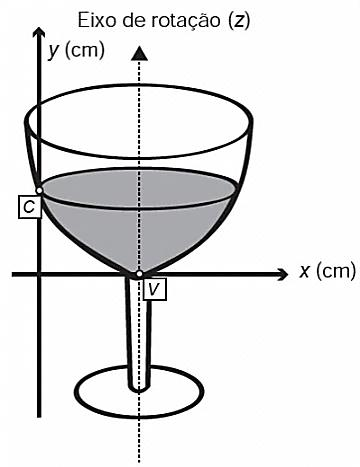
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei:
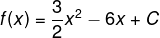
onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x. Nessas condições, a altura do líquido contido na taça, em centímetros, é
A) 1.
B) 2.
C) 4.
D) 5.
E) 6.
Alternativa E.
Como a função possui uma única raiz, então o valor de delta é zero, logo:
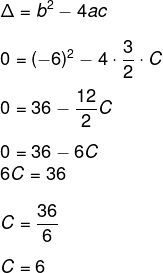
-
Questão 13
(Enem 2009) Um posto de combustível vende 10.000 litros de álcool por dia a R$ 1,50 cada litro. Seu proprietário percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 100 litros a mais por dia. Por exemplo, no dia em que o preço do álcool foi R$ 1,48, foram vendidos 10.200 litros.
Considerando x o valor, em centavos, do desconto dado no preço de cada litro, e V o valor, em R$, arrecadado por dia com a venda do álcool, então a expressão que relaciona V e x é:
A) V = 10.000 + 50x – x².
B) V = 10.000 + 50x + x².
C) V = 15.000 – 50x – x².
D) V = 15.000 + 50x – x².
E) V = 15.000 – 50x + x².
Alternativa C.
Sabemos que há um aumento de 100 litros vendidos a cada centavo de desconto, ou seja:
(10.000 + 100x)
Além disso, o valor pago pelo litro é dado por (1,50 – 0,01x). Calculando o valor V, temos que:
V = (10.000 + 100x) (1,50 - 0,01x)
V = 15.000 +150x – 100x – x²
V = 15.000 + 50x – x²
-
Questão 14
(Enem 2016) Um túnel deve ser lacrado com uma tampa de concreto. A seção transversal do túnel e a tampa de concreto têm contornos de um arco de parábola e mesmas dimensões. Para determinar o custo da obra, um engenheiro deve calcular a área sob o arco parabólico em questão. Usando o eixo horizontal no nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a seguinte equação para a parábola:
y = 9 – x², sendo x e y medidos em metros.
Sabe-se que a área sob uma parábola como esta é igual a 2/3 da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel.
Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
A) 18
B) 20
C) 36
D) 45
E) 54
Alternativa C.
Para calcular as dimensões do retângulo que contém a parábola, é necessário calcular a distância entre as raízes e também o valor da sua altura máxima, ou seja, yv.
Calculando as raízes, temos que:
y = 9 – x²
0 = 9 – x²
x² = 9
x = ± √9
x = ± 3
Sabemos que, de – 3 até 3, temos 6 unidades.
Agora calculando Δ e yv, temos que:
Δ = b² – 4ac
Δ = 0² – 4 ( – 1) ( 9)
Δ = 36
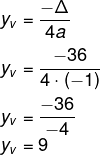
Por fim, sabemos que a área é 2/3 do produto entre 6 e 9:
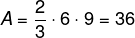
-
Questão 15
(Enem 2010) Um laticínio possui dois reservatórios de leite. Cada reservatório é abastecido por uma torneira acoplada a um tanque resfriado. O volume, em litros, desses reservatórios depende da quantidade inicial de leite no reservatório e do tempo t, em horas, em que as duas torneiras ficam abertas. Os volumes dos reservatórios são dados pelas funções V1(t) = 250t³ - 100t + 3000 e V2(t) = 150t³ + 69t + 3000.
Depois de aberta cada torneira, o volume de leite de um reservatório é igual ao do outro no instante t = 0 e, também, no tempo t igual a:
A) 1,3 h.
B) 1,69 h.
C) 10,0 h.
D) 13,0 h.
E) 16,9 h.
Alternativa A.
Faremos: V1(t) = V2(t).
250t³ - 100t + 3000 = 150t³ + 69t + 3000
100t³ - 169t = 0
Colocando t em evidência, temos que:
t (100t² – 169) = 0
Dividindo por t dos dois lados, temos que:
100t² – 169 = 0
100t² = 169
t² = 169/100
t = √(169/100)
t = 13/10
t = 1,3 horas
-
Questão 16
(Vunesp 2017) Uma função quadrática f é dada por f(x) = x² + bx + c, com b e c reais. Se f(1) = –1 e f(2) – f(3) = 1, o menor valor que f(x) pode assumir, quando x varia no conjunto dos números reais, é igual a:
A) – 12.
B) – 6.
C) – 10.
D) – 5.
E) – 9.
Alternativa D.
Sabemos que: f(2) – f(3) = 1.
2² + 2b + c – ( 3² + 3b + c) = 1
4 + 2b + c – 9 – 3b – c = 1
– 5 – b = 1
– b = 1 + 5
– b = 6 ( – 1)
b = – 6
Além disso, temos que:
Se f(1) = –1
f(1) = –1
1² + b·1 + c = – 1
1+ b + c = – 1
b+c = – 1 – 1
b + c = – 2
Então, c = – b – 2.
Sendo b = – 6, temos que:
c = – b – 2
c = – ( – 6) – 2
c = 6 – 2
c = 4
Então, a lei de formação da função é f(x) = x² – 6x + 4.
Para encontrar o mínimo dessa função, calcularemos delta e yv
Δ = b² – 4ac
Δ = 6² - 4.1.4 = 36 – 16 = 20
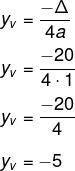
-
Questão 17
(UFRGS 2018) As raízes da equação 2x² + bx + c = 0 são 3 e − 4. Nesse caso, o valor de b - c é:
A) −26.
B) −22.
C) −1.
D) 22.
E) 26.
Alternativa E.
Sabemos que a = 2 e que a equação pode ser reescrita como:
a(x – x1) ( x – x2) = 0
Como conhecemos as duas raízes da equação, temos que:
2(x – 3) ( x + 4) = 0
2(x² +4x – 3x – 12) = 0
2(x² + x – 12) = 0
2x² + 2x – 24 = 0
Agora basta calcular: b – c = 2 – ( – 24) = 2 + 24 = 26.
-
Questão 18
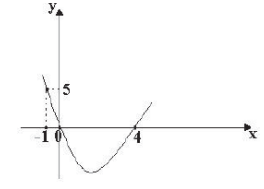
(Consulplan – Mossoró/RN) Qual é a soma dos coeficientes da função polinomial do 2º grau cujo gráfico está representado abaixo?
A) – 4
B) 2
C) 7
D) – 1
E) – 3
Alternativa E.
Como o gráfico é uma parábola, então podemos descrevê-lo como uma equação do tipo f(x) = ax² + bx + c.
Analisando o gráfico, é possível perceber que os pontos (0,0); (– 1, 5) e (4,0) pertencem à parábola. Então, sabemos que 0 e 4 são as raízes da equação:
f(x) = a( x – 0) ( x – 4)
f(x) = ax(x – 4)
f(x) = ax² – 4ax
Por outro lado, sabemos que f(– 1) = 5.
5 = a · (– 1) ² – 4 · a · ( – 1)
5 = a + 4a
5 = 5a
a = 5/5
a = 1
Conhecendo o valor de a, então a função será:
f(x) = x² – 4x
Sendo assim, o valor de a + b + c = 1 – 4 + 0 = – 3.
-
Questão 19
(Enem 2018) Um projétil é lançado por um canhão e atinge o solo a uma distância de 150 metros do ponto de partida. Ele percorre uma trajetória parabólica, e a altura máxima que atinge em relação ao solo é de 25 metros.
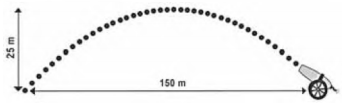
Admita um sistema de coordenadas xy em que no eixo vertical y está representada a altura e no eixo horizontal x está representada a distância, ambas em metro. Considere que o canhão está no ponto (150; 0) e que o projétil atinge o solo no ponto (0; 0) do plano xy.
A equação da parábola que representa a trajetória descrita pelo projétil é:
A) y = 150x – x²
B) y = 3 750x – 25x²
C) 75y = 300x – 2x²
D) 125y = 450x – 3x²
E) 225y = 150x – x²
Alternativa E.
Sabemos que:
y = a( x – 0) ( x – 150)
y = ax(x – 150)
y = ax² – 150ax
Na metade do percurso, ela atinge sua altura máxima, ou seja, f(75) = 25. Então, temos que:

Substituindo o valor de a na equação, temos que:
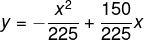
Multiplicado por 225 e reordenando os termos, encontraremos:
225y = 150x – x²
-
Questão 20
(Enem 2020) Uma empresa de chocolates consultou o gerente de produção e verificou que existem cinco tipos diferentes de barras de chocolate que podem ser produzidas, com os seguintes preços no mercado:
• Barra I: R$ 2,00;
• Barra II: R$ 3,50;
• Barra III: R$ 4,00;
• Barra IV: R$ 7,00;
• Barra V: R$ 8,00.
Analisando as tendências do mercado, que incluem a quantidade vendida e a procura pelos consumidores, o gerente de vendas da empresa verificou que o lucro L com a venda de barras de chocolate é expresso pela função L(x) = – x² + 14x – 45, em que x representa o preço da barra de chocolate.
A empresa decide investir na fabricação da barra de chocolate cujo preço praticado no mercado renderá o maior lucro. Nessas condições, a empresa deverá investir na produção da barra:
A) I.
B) II.
C) III.
D) IV.
E) V.
Alternativa D.
Para encontrar o valor de x que maximiza o lucro, é necessário encontrar o valor de xv, então temos que: a = – 1, b = 14 e c = – 45.