Enem: lista de exercícios sobre estatística (moda, média e mediana)
Com esta lista de exercícios, você testará seus conhecimentos sobre moda, média e mediana, medidas utilizadas para analisar o comportamento de dados estatísticos.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
(Enem 2019) O quadro apresenta a quantidade de um tipo de pão vendido em uma semana em uma padaria.
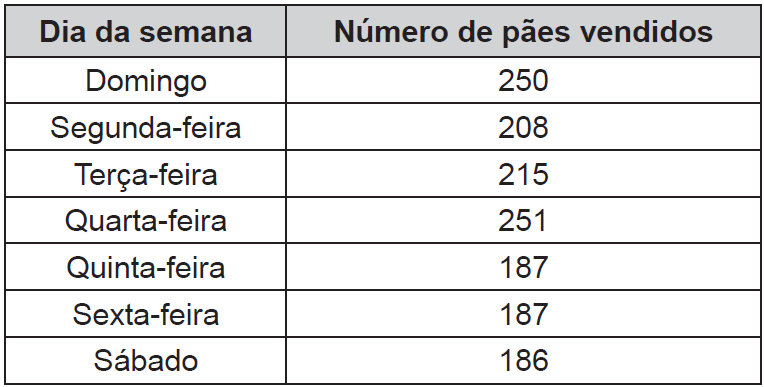
O dono da padaria decidiu que, na semana seguinte, a produção diária desse tipo de pão seria igual ao número de pães vendidos no dia da semana em que tal quantidade foi a mais próxima da média das quantidades vendidas na semana.
O dia da semana utilizado como referência para a quantidade de pães a serem produzidos diariamente foi
A) domingo.
B) segunda-feira.
C) terça-feira.
D) quarta-feira.
E) sábado.
Alternativa C
Calculando a média, temos que:
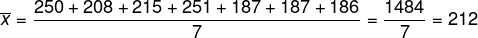
O valor mais próximo de 212 é encontrado na terça-feira, de 215 pães.
-
Questão 2
(Enem 2019) Em uma fábrica de refrigerantes, é necessário que se faça periodicamente o controle no processo de engarrafamento para evitar que sejam envasadas garrafas fora da especificação do volume escrito no rótulo. Diariamente, durante 60 dias, foram anotadas as quantidades de garrafas fora dessas especificações. O resultado está apresentado no quadro.

A média diária de garrafas fora das especificações no período considerado é
A) 0,1.
B) 0,2.
C) 1,5.
D) 2,0.
E) 3,0.
Alternativa B
Calculando a média, temos que:
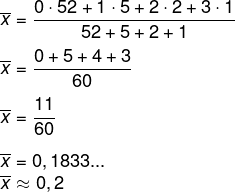
-
Questão 3
(Enem 2019) O quadro apresenta a relação dos jogadores que fizeram parte da Seleção Brasileira de voleibol masculino nas Olimpíadas de 2012, em Londres, e suas respectivas alturas, em metro.
Disponível em: www.cbv.com.br. Acesso em: 31 jul. 2012 (adaptado).
A mediana das alturas, em metro, desses jogadores é
A) 1,90.
B) 1,91.
C) 1,96.
D) 1,97.
E) 1,98.
Alternativa C
Calculando a mediana das alturas, temos que colocar os dados em ordem e encontrar os elementos centrais:
1,84 - 1,90 - 1,90 - 1,91 - 1,92 - 1,94 - 1,98 - 2,01 - 2,03 - 2,05 - 2,09 - 2,11
Somando os 2 termos centrais e dividindo por 2:
(1,94 + 1,98): 2 = 1,96
-
Questão 4
(Enem 2017)
O gráfico apresenta a taxa de desemprego (em %) para o período de março de 2008 a abril de 2009, obtida com base nos dados observados nas regiões metropolitanas de Recife, Salvador, Belo Horizonte, Rio de Janeiro, São Paulo e Porto Alegre.
IBGE. Pesquisa mensal de emprego. Disponível em: www.ibge.gov.br. Acesso em: 30 jul. 2012 (adaptado).
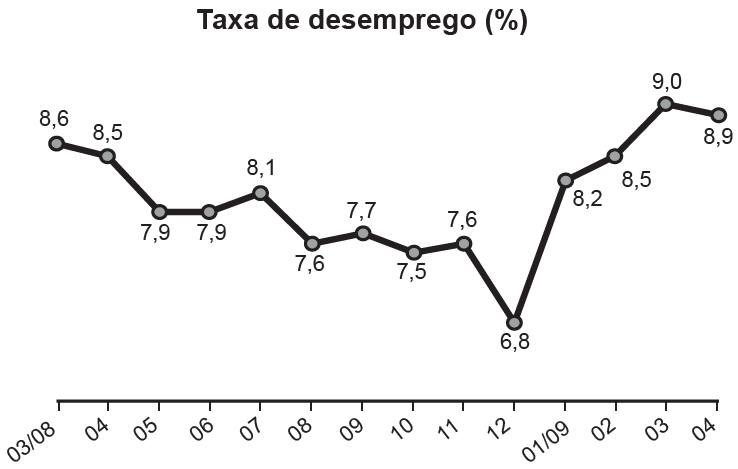
A mediana dessa taxa de desemprego, no período de março de 2008 a abril de 2009, foi de
A) 8,1%.
B) 8,0%.
C) 7,9%.
D) 7,7%.
E) 7,6%.
Alternativa B
Primeiro colocaremos os dados em ordem e encontraremos os termos centrais:
6,8; 7,5; 7,6; 7,6; 7,7; 7,9; 7,9; 8,1; 8,2; 8,5; 8,5; 8,6; 8,9; 9,0.
Calculando a média entre esses valores, (7,9 + 8,1) : 2 = 16 : 2 = 8.
-
Questão 5
(Enem 2016) Ao iniciar suas atividades, um ascensorista registra tanto o número de pessoas que entram quanto o número de pessoas que saem do elevador em cada um dos andares do edifício onde ele trabalha. O quadro apresenta os registros do ascensorista durante a primeira subida do térreo, de onde partem ele e mais três pessoas, ao quinto andar do edifício.

Com base no quadro, qual é a moda do número de pessoas no elevador durante a subida do térreo ao quinto andar?
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa D
Vejamos o número de pessoas em cada andar:
Térreo: 4 pessoas
1º andar: 4 + 4 – 3 = 5 pessoas
2º andar: 5 + 1 – 1 = 5 pessoas
3º andar: 5 + 2 – 2 = 5 pessoas
4º andar: 5 + 2 – 0 = 7 pessoas
5º andar: 7 + 2 – 6 = 3 pessoas
A moda da quantidade de pessoas é 5.
-
Questão 6
(Enem 2016) Um posto de saúde registrou a quantidade de vacinas aplicadas contra febre amarela nos últimos cinco meses:
-
1º mês: 21;
-
2º mês: 22;
-
3º mês: 25;
-
4º mês: 31;
-
5º mês: 21.
No início do primeiro mês, esse posto de saúde tinha 228 vacinas contra febre amarela em estoque. A política de reposição do estoque prevê a aquisição de novas vacinas no início do sexto mês, de tal forma que a quantidade inicial em estoque para os próximos meses seja igual a 12 vezes a média das quantidades mensais dessas vacinas aplicadas nos últimos cinco meses.
Para atender essas condições, a quantidade de vacinas contra febre amarela que o posto de saúde deve adquirir no início do sexto mês é
A) 156.
B) 180.
C) 192.
D) 264.
E) 288.
Alternativa B
O total de vacinas aplicadas foi igual a:
21 + 22 + 25 + 31 + 21 = 120
Restou um total de 228 – 120 = 108 vacinas.
A média de vacinas mensal é igual a 120 : 5 = 24 vacinas/mês. Como queremos 12 vezes a média dos 5 primeiros meses, será o total de 12 · 24 = 288 vacinas, então, é necessário adquirir um total de 288 – 108 = 180 vacinas.
-
-
Questão 7
(Enem 2016) Em uma cidade, o número de casos de dengue confirmados aumentou consideravelmente nos últimos dias. A prefeitura resolveu desenvolver uma ação contratando funcionários para ajudar no combate à doença, os quais orientarão os moradores a eliminarem criadouros do mosquito Aedes aegypti, transmissor da dengue. A tabela apresenta o número atual de casos confirmados, por região da cidade.
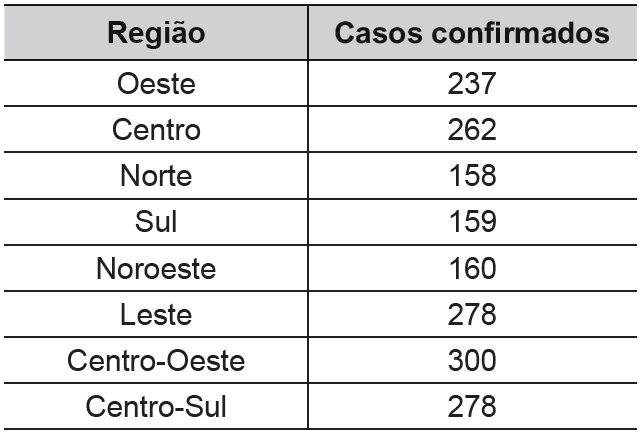
A prefeitura optou pela seguinte distribuição dos funcionários a serem contratados:
I. 10 funcionários para cada região da cidade cujo número de casos seja maior que a média dos casos confirmados.
II. 7 funcionários para cada região da cidade cujo número de casos seja menor ou igual à média dos casos confirmados.
Quantos funcionários a prefeitura deverá contratar para efetivar a ação?
A) 59
B) 65
C) 68
D) 71
E) 80
Alternativa D
Calculando a média, temos que:
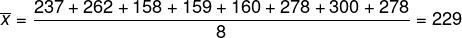
Analisando as 8 regiões, é possível perceber que 5 estão acima da média e outras 3 estão abaixo, o total de funcionários é dado então por:
5 · 10 + 7 · 3 = 50 + 21 = 71 funcionários
-
Questão 8
(Enem) A tabela a seguir mostra a evolução da receita bruta anual nos três últimos anos de cinco microempresas (ME) que se encontram à venda.
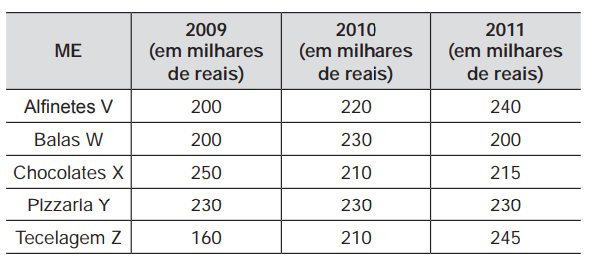
Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual.
As empresas que este investidor escolhe comprar são
A) Balas W e Pizzaria Y.
B) Chocolates X e Tecelagem Z.
C) Pizzaria Y e Alfinetes V.
D) Pizzaria Y e Chocolates X.
E) Tecelagem Z e Alfinetes V.
Alternativa D
Calculando a média, temos que:
-
Alfinetes V = (200 + 220 + 240) : 3 = 220
-
Balas W = (200 + 230 + 200) : 3 = 210
-
Chocolates X = (250 + 210 + 215) : 3 = 225
-
Pizzaria Y = (230 +230 + 230) : 3 = 230
-
Tecelagem Z = (160 + 210 + 245) : 3 = 205
Sendo assim, as duas empresas com maior média são Pizzaria Y e Chocolates X.
-
-
Questão 9
(Enem) O gráfico apresenta o comportamento de emprego formal surgido, segundo o CAGED, no período de janeiro de 2010 a outubro de 2010.
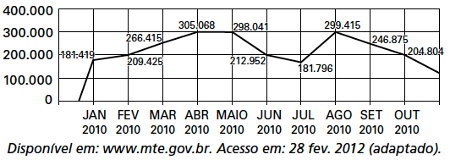
Com base no gráfico, o valor da parte inteira da mediana dos empregos formais surgidos no período é
A) 212.952
B) 229.913
C) 240.621
D) 255.496
E) 298.041
Alternativa B
Colocando os dados em ordem, temos que:
181.419, 181.796, 204.804, 209.425, 212.952, 246.875, 266.415, 298.041, 299.415, 305.068
Como há 10 elementos, os termos centrais são os valores destacados em vermelho, que são o 5° e 6° da sequência.
Calculando a média entre eles, temos que:
(212.952 + 246.875) : 2 = 229.913,5
Então, a parte inteira da mediana é 229.913.
-
Questão 10
(Enem) Uma loja que vende sapatos recebeu diversas reclamações de seus clientes relacionadas à venda de sapatos de cor branca ou preta. Os donos da loja anotaram as numerações dos sapatos com defeito e fizeram um estudo estatístico com intuito de reclamar com o fabricante.
A tabela contém a média, a mediana e a moda desses dados anotados pelos donos.

Para quantificar os sapatos pela cor, os donos representaram a cor branca pelo número 0 e a cor preta pelo número 1. Sabe-se que a média da distribuição desses zeros e uns é igual a 0,45.
Os donos da loja decidiram que a numeração dos sapatos com maior número de reclamações e a cor com maior número de reclamações não serão mais vendidas.
A loja encaminhou um ofício ao fornecedor dos sapatos, explicando que não serão mais encomendados os sapatos de cor
A) branca e os de número 38.
B) branca e os de número 37.
C) branca e os de número 36.
D) preta e os de número 38.
E) preta e os de número 37.
Alternativa A
Como a moda é 38, significa que é o valor mais recorrente de sapatos com defeitos. Sobre a cor, como a distribuição entre 0 e 1, sendo 0 para branca e 1 para preta, possui média mais próxima de 0 do que de 1, isso significa que há mais sapatos brancos defeituosos, então, não serão mais encomendados os sapatos da cor branca e os de número 38.
-
Questão 11
(Enem) Uma equipe de especialistas do centro meteorológico de uma cidade mediu a temperatura do ambiente, sempre no mesmo horário, durante 15 dias intercalados, a partir do primeiro dia de um mês. Esse tipo de procedimento é frequente, uma vez que os dados coletados servem de referência para estudos e verificação de tendências climáticas ao longo dos meses e anos.
As medições ocorridas nesse período estão indicadas no quadro:
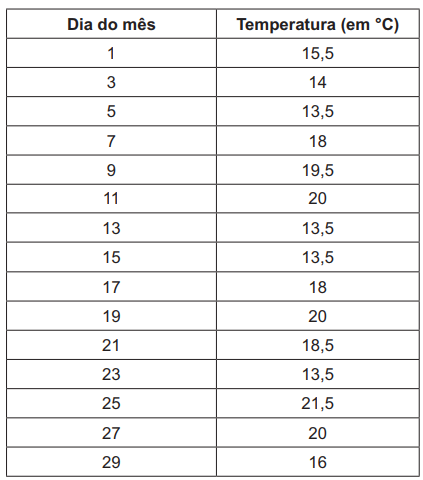
Em relação à temperatura, os valores da média, mediana e moda são, respectivamente, iguais a
A) 17 °C, 17 °C e 13,5 °C.
B) 17 °C, 18 °C e 13,5 °C.
C) 17 °C, 13,5 °C e 18 °C.
D) 17 °C, 18 °C e 21,5 °C.
E) 17 °C, 13,5 °C e 21,5 °C.
Alternativa B
Note que, em todas as afirmativas, o primeiro valor é 17°, logo, a média é igual a 17. Podemos realizar o cálculo da mediana:
13,5; 13,5; 13,5; 13,5; 14; 15,5; 16; 18; 18; 18,5; 19,5; 20; 20; 20; 21,5
A mediana é igual a 18.
Com relação à moda, o valor mais recorrente nessa distribuição é 13,5.
-
Questão 12
(Enem 2021) O técnico de um time de basquete pretende aumentar a estatura média de sua equipe de 1,93 m para, no mínimo, 1,99 m. Para tanto, dentre os 15 jogadores que fazem parte de sua equipe, substituirá os quatro mais baixos, de estaturas: 1,78 m, 1,82 m, 1,84 m e 1,86 m. Para isso, o técnico contratou um novo jogador de 2,02 m. Os outros três jogadores que ele ainda precisa contratar devem satisfazer à sua necessidade de aumentar a média das estaturas da equipe. Ele fixará a média das estaturas para os três jogadores que ainda precisa contratar dentro do critério inicialmente estabelecido.
Qual deverá ser a média mínima das estaturas, em metro, que ele deverá fixar para o grupo de três novos jogadores que ainda contratará?
A) 1,96
B) 1,98
C) 2,05
D) 2,06
E) 2,08
Alternativa E
Se a média atual é 1,93, então sabemos que a soma das 15 alturas é igual a 1,93 · 15 = 28,95 metros.
Subtraindo as 4 alturas dos jogadores que foram substituídos e acrescentando a altura do outro jogador, temos que:
28,95 + 2,02 – 1,78 – 1,82 – 1,84 – 1,86 = 23,67
Além disso, serão contratados outros 3 jogadores com altura x, y z, e queremos que a média de altura seja 1,99, então, temos que:
(23,67 + x + y + z) : 15 = 1,99
23,67 + x + y + z = 1,99 · 15
23,67 + x + y + z = 29,85
x + y + z = 29,85 – 23,67
x + y + z = 6,18
Para encontrar a média da altura desses três jogadores, basta dividir por três: 6,18 : 3 = 2,06.
-
Questão 13
(Enem – PPL – 2017) Numa turma de inclusão de jovens e adultos na educação formal profissional (Proeja), a média aritmética das idades dos seus dez alunos é de 32 anos. Em determinado dia, o aluno mais velho da turma faltou e, com isso, a média aritmética das idades dos nove alunos presentes foi de 30 anos.
Disponível em: http://portal.mec.gov.br. Acesso em: 10 mar. 2012 (adaptado).
Qual é a idade do aluno que faltou naquela turma?
A) 18
B) 20
C) 31
D) 50
E) 62
Alternativa D
Sabemos que a média das idades é igual a 32. Seja S1 a soma das alturas dos 10 alunos, sabemos que:
S1 : 10 = 32
S1 = 32 · 10
S1 = 320
Quando esse aluno falta, a média é de 30, então, sabemos que:
S2 : 9 = 30
S2 = 30 · 9
S2 = 270
Assim, calculando a diferença entre as somas:
320 – 270 = 50 anos
-
Questão 14
(Enem 2015) Em uma seletiva para a final dos 100 metros livres de natação, numa olimpíada, os atletas, em suas respectivas raias, obtiveram os seguintes tempos:
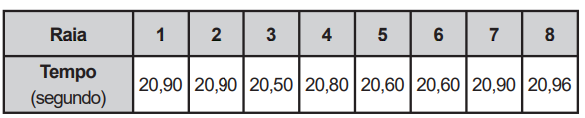
A mediana dos tempos apresentados no quadro é
A) 20,70.
B) 20,77.
C) 20,80.
D) 20,85.
E) 20,90.
Alternativa D
Primeiro colocaremos os dados em ordem e encontraremos os dois termos centrais.
20,50; 20,60; 20,60; 20,80; 20,90; 20,90; 20,90; 20,96.
A média entre esses termos é (20,80 + 20,90) : 2 = 20,85.
-
Questão 15
(Enem 2016) A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanece no cargo, caso contrário, ele será despedido. O quadro mostra o lucro mensal, em milhares de reais, dessa empresa, de janeiro a maio do ano em curso.

Qual deve ser o lucro mínimo da empresa no mês de junho, em milhares de reais, para o gerente continuar no cargo no próximo semestre?
A) 26
B) 29
C) 30
D) 31
E) 35
Alternativa E
A média entre os 6 meses tem que ser pelo menos igual a 30. Seja x o faturamento do mês de junho, então, temos que:
(21 + 35 + 21 + 30 + 38 + x) : 6 = 30
(145 + x) : 6 = 30
145 + x = 30 · 6
145 + x = 180
x = 180 – 145
x = 35
-
Questão 16
(Enem) O quadro seguinte mostra o desempenho de um time de futebol no último campeonato. A coluna da esquerda mostra o número de gols marcados e a coluna da direita informa em quantos jogos o time marcou aquele número de gols.
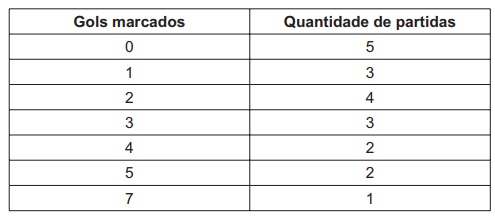
Se X, Y e Z são, respectivamente, a média, a mediana e a moda dessa distribuição, então
A) X = Y < Z.
B) Z < X = Y.
C) Y < Z < X.
D) Z < X < Y.
E) Z < Y < X.
Alternativa E
Primeiro calcularemos a média:
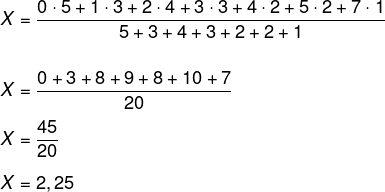
Agora encontraremos a mediana.
Como há 20 valores, então a mediana será a média entre o 10º e o 11º valor.
Analisando os resultados na tabela, sabemos que a média entre o 10º e 11º será a mediana. Para encontrar esses valores, basta analisar a lista. O 0 aparece 5 vezes, então, do 1º ao 5º termo, será 0; do 6º ao 8º, será 1; e do 9º até o 12º, será 2. Dessa forma, o 10º e 11º termos são iguais a 2, logo, temos que:
Y = (2 + 2) : 2 = 2
Por fim, a moda de um conjunto é o valor que tem maior frequência, então, temos Z = 0.
Assim, temos que Z < Y < X.
-
Questão 17
(Enem) Depois de jogar um dado em forma de cubo e de faces numeradas de 1 a 6, por 10 vezes consecutivas, e anotar o número obtido em cada jogada, construiu-se a seguinte tabela de distribuição de frequência:
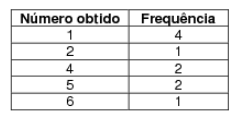
A média, mediana e moda dessa distribuição de frequência são, respectivamente:
A) 3, 2 e 1
B) 3, 3 e 1
C) 3, 4 e 2
D) 5, 4 e 2
E) 6, 2 e 4
Alternativa B
Calculando a média, temos que:
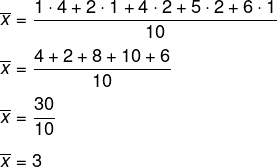
A mediana é a média dos dois termos centrais, que são o 5º e 6º valores. Analisando os resultados e as suas frequências, o 5º valor é 2 e o 6º é 4, então, (2 + 4) : 2 = 3.
Mediana = 3
Por fim, a moda é o valor com maior frequência, que, no caso, é o 1, então, a média, a mediana e a moda são, respectivamente, 3, 3 e 1.
-
Questão 18
(Enem 2017) Cinco regiões de um país estão buscando recursos no Governo Federal para diminuir a taxa de desemprego de sua população. Para decidir qual região receberia o recurso, foram colhidas as taxas de desemprego, em porcentagem, dos últimos três anos. Os dados estão apresentados na tabela.
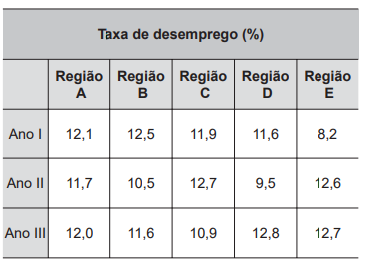
Ficou decidido que a região contemplada com a maior parte do recurso seria aquela com a maior mediana das taxas de desemprego dos últimos três anos.
A região que deve receber a maior parte do recurso é a
A) A.
B) B.
C) C.
D) D.
E) E.
Alternativa E
Calculando a mediana de cada uma delas, temos que:
Região A → Mediana: 12,0
Região B → Mediana: 11,6
Região C → Mediana: 11,9
Região D → Mediana: 11,6
Região E → Mediana: 12,6
Então, a região que deve receber a maior parte dos recursos é a E.
-
Questão 19
(FGV) Sejam os números 7, 8, 3, 5, 9 e 5 seis números de uma lista de nove números inteiros. O maior valor possível para a mediana dos nove números da lista é
A) 5
B) 6
C) 7
D) 8
E) 9
Alternativa D
Seja x, y e z os números que faltam na lista, para que esse conjunto tenha a maior mediana possível, x, y e z devem ser números maiores ou iguais a 9, então, a sequência ficaria:
3, 5, 5, 7, 8, 9, X, Y, Z
O termo central dessa sequência é o número 8, assim, a mediana do conjunto é 8.
-
Questão 20
(Fundatec) Se a mediana de um determinado processo for igual a 7, isso quer dizer que:
A) O 7º valor da amostra representará a mediana.
B) O 7º valor da amostra ordenada representará a mediana.
C) A posição mediana é 7.
D) 50% dos valores da amostra são iguais a 7.
E) 50% dos valores da amostra são menores ou iguais a 7.
Alternativa D
Analisando as alternativas, a correta é a D. Acontece que a mediana é o termo central do conjunto com os elementos em ordem, o que significa que metade dos termos é menor ou igual à mediana, e a outra metade, maior ou igual à mediana.