Exercícios sobre área do setor circular
Um setor circular possui raio medindo 6 cm e ângulo central igual a 72°. Sua área, em cm², é igual a:
A)\(\ \ 5,0\ \pi\)
B) \(6,8\ \pi\)
C) \(\ 7,2\ \pi\)
D) \(\ \ 8,0\ \pi\)
E) \(\ \ 8,4\ \pi\)
Alternativa C
Calculando a área do setor circular:
\(A=\frac{\theta⋅π⋅ {r} ^ {2}} {360°}\)
\(A=\frac{72\cdot\pi\cdot6^2}{360}\)
\(A=\frac{72\cdot\pi\cdot36}{360}\)
\(A=\frac{72\cdot\pi}{10}\)
\(A=7,2\pi\ \ cm^2\)
Um setor circular possui arco medindo \(\frac{\pi}{8}rad\) e raio igual a 4 cm. Sua área é igual a:
A) \(2\pi\) cm²
B) \(\pi\ \) cm²
C) 0,5 \(\pi\ \) cm²
D) 0,3 \(\pi\ \) cm²
E) 0,2 \(\pi\ \)cm²
Alternativa B
Calculando a área do setor circular em função do comprimento do arco:
\(A=\frac{c\cdot r^2}{2}\)
\(A=\frac{\frac{\pi}{8}\cdot4^2}{2}\ \)
\(A=\frac{\frac{16\pi}{8}}{2}\)
\(A=\frac{2\pi}{2}\)
\(A=\pi cm^2\)
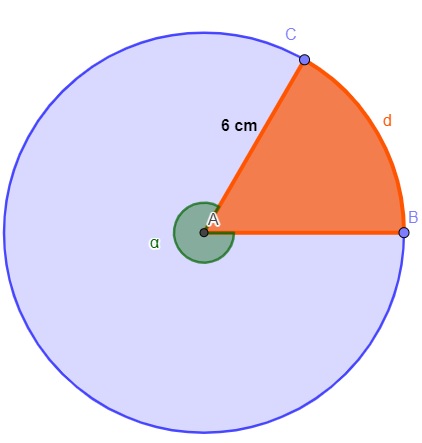
Na imagem a seguir, há em destaque um setor circular que possui área igual a \(6\pi\ cm^2\). O ângulo α mede:
A) 60°
B) 120°
C) 240°
D) 300°
E) 330°
Alternativa D
Sabemos que:
\(A=\frac{\theta\cdot\pi\cdot r^2}{360}\)
Vale lembrar que θ é o ângulo central do setor circular. Como conhecemos o valor da área:
\(6\pi=\frac{\theta\cdot\pi\cdot6^2}{360}\)
\(6\pi=\frac{\theta\cdot\pi\cdot36}{360}\)
Simplificando o numerador e o denominador por 36:
\(6\pi=\frac{\theta\cdot\pi}{10}\)
\(6\pi\cdot10\ =\ \theta\pi\)
\(60\pi=\ \theta\pi\)
\(\theta=\ 60° \)
Sabemos que o ângulo α junto ao ângulo θ formam 360°, então:
\(\alpha+\ 60° = 360°\)
\(\alpha=\ 360° - 60° \)
\(\alpha=\ 300° \)
O raio de um setor circular que possui comprimento de arco igual a \(\frac{\pi}{6}\) cm e área igual a \(\pi\) cm² é igual a:
A) 6 cm
B) 8 cm
C) 10 cm
D) 12 cm
E) 14 cm
Alternativa D
Sabemos que:
\(A=\frac{c\cdot r}{2}\ \ \)
\(\pi=\frac{\frac{\pi}{6}\cdot r}{2}\)
\(2\pi=\frac{\pi}{6}\cdot r\ \)
\(2\ \cdot6\pi=\ \pi r\)
\(12\pi=\ \pi r\)
\(r\ =\ 12\)
Um setor circular possui raio igual a 5 cm e área igual a 25 cm². Sendo π = 3, a medida do ângulo central desse setor circular é de:
A) 100°
B) 120°
C) 150°
D) 180°
E) 210°
Alternativa B
Sabemos que:
\(A=\frac{\theta\cdot\pi\cdot r^2}{360}\)
\(25=\frac{\theta\cdot3\cdot5^2}{360}\)
\(25=\frac{\theta\cdot3\cdot25}{360}\)
Simplificando o numerador e o denominador por 36:
\(25=\frac{\theta\cdot75}{360}\)
\(25\cdot360\ =\ \theta\ \cdot75\)
\(9000=\ 75\theta\)
\(\theta=\frac{9000}{75}\)
\(\theta=\ 120° \)
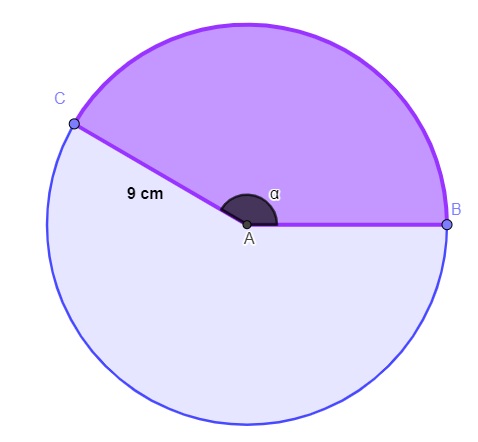
Sabendo que α= 150° e que π= 3,1, a área do setor circular a seguir será de, aproximadamente:
A) 105 cm²
B) 110 cm²
C) 112 cm²
D) 115 cm²
E) 118 cm²
Alternativa A
\(A=\frac{\theta\cdot\pi r^2}{360}\)
\(A=\frac{150\cdot3,1\cdot9^2}{360}\)
\(A=\frac{150\cdot3,1\cdot81}{360}\)
\(A=\frac{37665}{360}\)
\(A\ =\ 104,625\) cm²
Portanto, a área é de aproximadamente 105 cm².
Analise o setor circular a seguir:
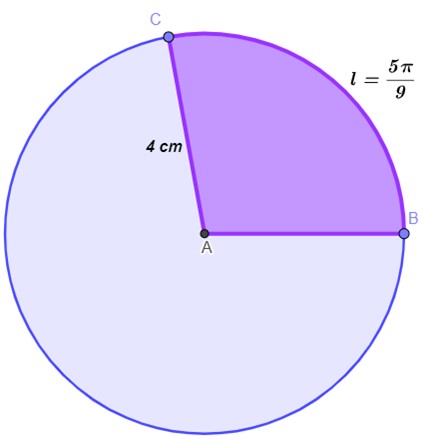
A sua área é de:
A) \(\ A=\frac{2\pi}{5}\ cm²\)
B) \(A=\frac{\pi}{3}\ cm²\)
C) \(A=\frac{5\pi}{6}\ cm²\)
D) \(A=\frac{5\pi}{3}\ cm²\)
Alternativa D
Conhecemos o comprimento do arco e o raio. Logo, temos que:
\(A=\frac{l\cdot r}{2}\)
\(A=\frac{\frac{5\pi}{6}\cdot4}{2}\)
\(A=\frac{\frac{20\pi}{6}}{2}\)
\(A=\frac{20\pi}{12}\)
\(A=\frac{5\pi}{3}cm^2\)
(FCC 2015) A partir do centro de uma torta circular retira-se uma fatia (setor circular) que corresponde a 35% do total. A fatia retirada é um setor circular de ângulo central igual a
A) 70°
B) 63°
C) 145°
D) 234°
E) 126°
Alternativa E
Sabemos que a área é proporcional ao ângulo. Como a área do setor corresponde a 35% da área do setor circular:
\(360° ⋅0,35 = 126°\)
Seu Joaquim decidiu dividir o seu terreno, que possui formato de círculo, entre os seus três filhos. Marcelo, o mais velho, ficou com uma área de 150,72 m². Utilizando π = 3,14 e sabendo que o ângulo central da região destinada a Marcelo é de 120°, qual é o valor do raio do setor circular correspondente à área destinada a ele?
A) 5
B) 6
C) 8
D) 10
E) 12
Alternativa E
\(A=\frac{\theta\cdot\pi r^2}{360}\)
\(150,72=\frac{120\cdot3,14\cdot r^2}{360}\)
\(150,72\cdot360=376,8r^2\)
\(54259,1=376,8r^2\)
\(r^2=\frac{54259,2}{376,8}\)
\(r^2=144\)
\(r=\sqrt{144}\)
\(r\ =\ 12\ \)
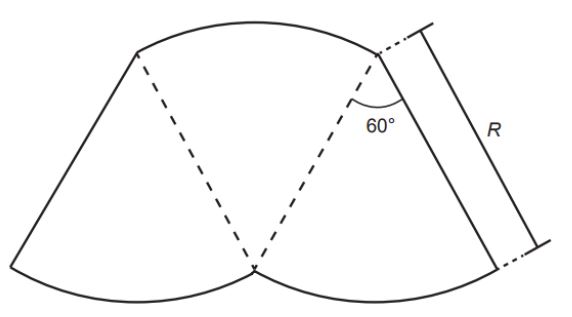
(Enem 2015) O proprietário de um parque aquático deseja construir uma piscina em suas dependências. A figura representa a vista superior dessa piscina, que é formada por três setores circulares idênticos, com ângulo central igual a 60°. O raio R deve ser um número natural.
O parque aquático já conta com uma piscina em formato retangular com dimensões 50 m x 24 m. O proprietário quer que a área ocupada pela nova piscina seja menor que a ocupada pela piscina já existente. Considere 3,0 como aproximação para π.
O maior valor possível para R, em metros, deverá ser
A) 16
B) 28
C) 29
D) 31
E) 49
Alternativa B
Sabemos que a área da nova piscina deve ser menor que a da retangular. A área da piscina existente é de:
\(A_a=50\cdot24=1200m^2\)
Note que há 3 setores circulares, logo, a área da nova piscina será de:
\(A_n=3\cdot\frac{60\cdot3\cdot R^2}{360}\)
\(A_n=\ 3\ \cdot\frac{180R^2}{360}\)
\(A_n=3\cdot\frac{R^2}{2}\)
\(A_n=\frac{3R^2}{2}\)
Sabemos que \(A_n<A_a\):
\(\frac{3R^2}{2}<1200\)
\(R^2<\frac{2\ \bullet\ 1200}{3}\)
\(R^2<800\)
\(R<\sqrt{800}\)
\(R\ <\ 28,28\ \)
Então, o maior raio possível é de 28 m.
(Uerj) Uma chapa de aço com a forma de um setor circular possui raio R e perímetro 3R, conforme ilustra a imagem.
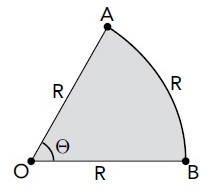
A área do setor equivale a:
A) R²
B) \(\frac{R^2}{4}\)
C) \(\frac{R^2}{2}\)
D) \(\frac{3R^2}{2}\)
Alternativa C
Conhecemos o comprimento do arco e o raio:
\(A=\frac{c\cdot r}{2}\)
\(A=\frac{R\cdot R}{2}\)
\(A=\frac{R^2}{2}\)
(Idecan 2016) Uma pista de corrida foi construída com o formato de um setor circular, conforme apresentado a seguir.
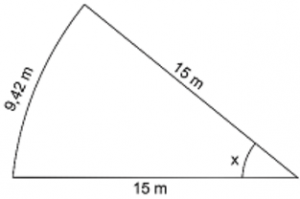
Pode‐se afirmar que o valor do ângulo x é igual a
(Considere: π = 3,14)
A) 30°
B) 36°
C) 42°
D) 45°
Alternativa B
Sabemos que:
360 — 2πr
x — 9,42
Multiplicando cruzado:
\(2\pi r\ x\ =\ 360\ \cdot9,42\)
Substituindo o valor do raio r = 15 e de π= 3,14:
\(2\ \cdot3,14\ \cdot15\ \cdot x\ =\ 3391,2\)
\(94,2x\ =\ 3391,2\)
\(x=\frac{3391,2}{94,2}\)
\(x\ =\ 36\)
