Exercícios sobre áreas de figuras planas
Em um terreno retangular, com 25 metros de comprimento e 36 metros de largura, será separada uma região com o formato de um quadrado de lado medindo 7 metros para a construção de um jardim. A área restante do terreno mede:
A) 951
B) 949
C) 900
D) 851
E) 849
Um terreno possui formato de um trapézio, com bases medindo 15 metros e 20 metros e a altura medindo 10 metros. Se a metade desse terreno será utilizada para a construção de uma casa, então a área construída desse terreno é de:
A) 175,0 m²
B) 105,5 m²
C) 87,5 m²
D) 82,5 m²
E) 78,0 m²
Alternativa C
Calculando a área do trapézio, temos que:
\(A=\frac{(B+b)⋅h}2\)
\(A=\frac{(15+20)⋅10}2\)
\(A=\frac{35⋅10}2\)
\(A=\frac{350}2\)
\(A=175\ m^2\)
A construção ocupa a metade dessa área, então a área construída é de:
\(175∶2=87,5\)
A área de um quadrado é de 2,56 m². Nessas condições, podemos afirmar que a medida do seu lado é de:
A) 1,28 m²
B) 1,44 m²
C) 1,55 m²
D) 1,60 m²
E) 1,80 m²
Alternativa D
Sabemos que a área do quadrado é igual ao quadrado seu lado:
\(A=l^2\)
\(2,56=l^2\)
\(l=\sqrt{2,56}\)
\(l=1,6\ m \)
No projeto da casa de Kárita há o desenho de uma área de lazer no formato de um quadrado, com 8 metros de lado. Nessa área de lazer haverá uma piscina circular com 4 metros de diâmetro, e a área restante será utilizada para a construção de um espaço de confraternização. Nessas condições, a área do espaço de confraternização medirá: (Use π = 3.)
A) 52 metros
B) 64 metros
C) 32 metros
D) 26 metros
E) 18 metros
Alternativa A
A medida da área do espaço de confraternização é a diferença entre a área do quadrado de lado medindo 8 metros e a área do círculo de diâmetro medindo 4 metros. Como o diâmetro é de 4 metros, o raio é de 2 metros. Calculando as áreas, temos que a área da área de lazer \(A_L \) é:
\(A_L=l^2\)
\(A_L=8^2=64\)
A área da piscina que possui formato de um círculo Ap é:
\(A_p=πr^2\)
\(A_p=3⋅2^2\)
\(A_p=3⋅4\)
\(A_p=12\)
Assim, a área restante é de: 64 – 12 = 52 metros.
Analise a imagem a seguir:
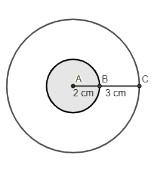
Podemos afirmar que a área branca mede:
A) 25π
B) 12π
C) 18π
D) 20π
E) 21π
Alternativa E
Para calcular a área da região branca, calcularemos a área do círculo maior \( A_M\) menos a área do círculo menor \(A_M\).
O raio do círculo maior é 2 + 3 = 5, portanto:
\(A_M=π⋅5^2=25π\)
O raio do círculo menor é 2, logo:
\(A_m=π⋅2^2=4π\)
A área branca mede 25 π – 4 π = 21 π.
A diagonal maior de um losango mede 18 cm, e a diagonal menor é \(\frac{2}{3}\) da diagonal maior, então a medida da área desse losango é de:
A) 108 cm²
B) 152 cm²
C) 164 cm²
D) 170 cm²
E) 177 cm²
Alternativa A
Calculando a medida da diagonal menor:
\(d=\frac{2}3⋅18\)
\(d=2⋅6=12\)
Calculando a área do losango:
\(A=\frac{12⋅18}2\)
\(A=\frac{216}2\)
\(A=108\ cm^2\)
Um objeto retangular possui área de 192 cm². Se a medida do comprimento desse objeto é de 16 cm, a medida da largura é:
A) 10 cm
B) 11 cm
C) 12 cm
D) 13 cm
E) 14 cm
Alternativa C
Sabemos que a área é de 192 cm², ou seja, A = 192. Como o comprimento é de 16 cm, para calcular a largura x temos que:
\(A=16⋅x\)
\(192=16⋅x\)
\(\frac{192}{16}=x\)
\(x=12\ cm\)
Marcelo e Renato herdaram de seu pai terrenos, cada um de mesma área. O terreno de Marcelo possui formato retangular com lados medindo 18 metros e 50 metros. Sabendo que o terreno de Renato é um quadrado, a medida do lado desse terreno é:
A) 12 metros
B) 15 metros
C) 20 metros
D) 25 metros
E) 30 metros
Alternativa E
Calculando a área do terreno de Marcelo:
\(A=18⋅50=900\)
Sabemos que a área do terreno de Renato é um quadrado de área igual a 900 m², portanto:
\(l^2=900\)
\(l=\sqrt{900}\)
\(l=30\ metros\)
(Enem 2016) Para garantir a segurança de um grande evento público que terá início às 4h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500 m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público.
Quantos policiais serão necessários no início do evento para garantir a segurança?
A) 360
B) 485
C) 560
D) 740
E) 860
Alternativa E
Sabemos que a área do espaço é de 500² = 250000 m².
Para cada m² há 4 pessoas, logo às 10 horas da manhã há um total de \(4⋅250000=1000000\) pessoas. Se a cada hora chegam 12000, até as 16 horas chegará um total de \(12000⋅6=720000\).
Assim, o número de pessoas é de 172000. Como haverá um policial para cada 2000 pessoas, temos que:
\(172000∶2000=860\) policiais
(Enem 2013) A cerâmica constitui-se em um artefato bastante presente na história da humanidade. Uma de suas várias propriedades é a retração (contração), que consiste na evaporação da água existente em um conjunto ou bloco cerâmico quando submetido a uma determinada temperatura elevada. Essa elevação de temperatura, que ocorre durante o processo de cozimento, causa uma redução de até 20% nas dimensões lineares de uma peça.
Disponível em: www.arq.ufsc.br. Acesso em: 3 mar. 2012
Suponha que uma peça, quando moldada em argila, possuía uma base retangular cujos lados mediam 30 cm e 15 cm. Após o cozimento, esses lados foram reduzidos em 20%. Em relação à área original, a área da base dessa peça, após o cozimento, ficou reduzida em
A) 4%
B) 20%
C) 36%
D) 64%
E) 96%
Alternativa D
Se houve uma redução de 20%, a nova medida dos lados representará 80% da medida anterior.
Sabemos que a área era de:
\(A=30⋅15\)
Entretanto, com a redução, os lados medirão 30 ⋅ 0,8 e 15 ⋅ 0,8. Logo, a nova área será de:
\(A_N=30⋅0,8⋅15⋅0,8\)
\(A_N=30⋅15⋅0,8⋅0,8\)
\(A_N=30⋅15⋅0,64\)
Sabemos que \(30⋅15=A\), então temos que:
\(A_N=A⋅0,64\)
Podemos concluir que a nova área é 64% da área antiga.
(IFG – Técnico Integrado 2016) Na fase final da construção de um ginásio, um pedreiro necessita ladrilhar o chão que representa uma base retangular, cujas dimensões são 18 metros e 32 metros. Os ladrilhos utilizados são quadrados com 24 centímetros de lado. O número de ladrilhos necessários para revestir o espaço é de
A) 100.000.
B) 10.000.
C) 1.000.
D) 100
Alternativa B
Para que os ladrilhos e o ginásio fiquem na mesma unidade de medida, transformaremos metros em centímetros, multiplicando por 100. Assim, a medida do ginásio em centímetros é 1800 cm e 3200 cm.
Calculando a área do ginásio:
\(A=1800⋅3200=5760000\)
A área do ladrilho é igual ao quadrado do lado, ou seja, 24² = 576.
Para saber quantos ladrilhos cabem no ginásio, basta dividir a área do ginásio pela área do ladrilho:
5760000 : 576 = 10000
(Enem 2015) Uma empresa de telefonia celular possui duas antenas que serão substituídas por uma nova, mais potente. As áreas de cobertura das antenas que serão substituídas são círculos de raio 2 km, cujas circunferências se tangenciam no ponto O como mostra a figura.
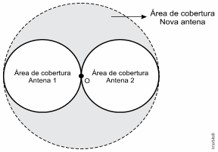
O ponto O indica a posição da nova antena, e sua região de cobertura será um círculo cuja circunferência tangenciará externamente as circunferências das áreas de cobertura menores.
Com a instalação da nova antena, a medida da área de cobertura, em quilômetros quadrados, foi ampliada em
A) 8?.
B) 12?.
C) 16?.
D) 32?.
E) 64?.
Alternativa A
Para encontrar a ampliação da área, calcularemos a diferença entre a área anterior e a nova área. Anteriormente, a área era a dos dois círculos menores com 2 km de raio.
\(A=2⋅πr^2\)
\(A=2⋅π⋅2^2\)
\(A=2⋅π⋅4\)
\(A=8π\)
Agora, sabemos que o novo raio é de 4 km, então:
\(A_2=π⋅4^2\)
\(A_2=16π\)
Calculando a diferença:
\(16π-8π=8π\)
