Exercícios sobre bissetriz
No ângulo AOC foi traçada a bissetriz OB, dividindo-o no ângulo AOB, com medida igual a 3x + 3°, e no BOC, medindo 4x – 6°. A medida do ângulo AOC é:
A) 9°
B) 15°
C) 30°
D) 45°
E) 60°
Alternativa E
Sabemos que o ângulo AOC é composto pelos ângulos AOB e BOC, que são congruentes:
\(4x-6=3x+3\ \)
\(4x-3x=3+6\)
\(x=9\)
Sabendo que x = 9:
\(4x-6=4\ \cdot9-6=36-6=30°\)
Como metade do ângulo AOC mede 30°, o ângulo AOC mede 60°.
Analise a imagem a seguir:
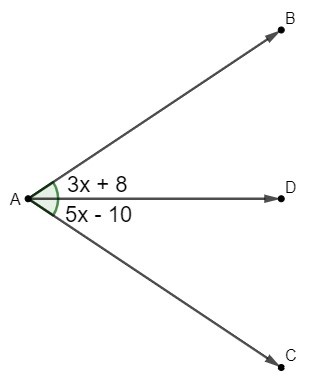
Sabendo que AD é a bissetriz do ângulo BAC, o valor de x é:
A) 6°
B) 7°
C) 8°
D) 9°
E) 10°
Alternativa D
Igualando os ângulos:
\(5x-10=3x+8\)
\(5x-3x=10+8\)
\(2x=18\)
\(x=\frac{18}{2}\)
\(x=9\)
Conhecemos como bissetriz:
A) A reta perpendicular ao lado do triângulo que passa pelo seu ponto médio.
B) A semirreta que divide um ângulo em dois ângulos congruentes.
C) O segmento de reta que liga o vértice do triângulo ao ponto médio do lado oposto.
D) O segmento de reta que é perpendicular a outro segmento de reta.
Alternativa B
A bissetriz é uma semirreta que divide um ângulo em dois ângulos congruentes, ou seja, com a mesma medida.
Os ângulos BAD e DAC são complementares. Sabendo que AD é a bissetriz do ângulo BAC, o valor de x + y é:
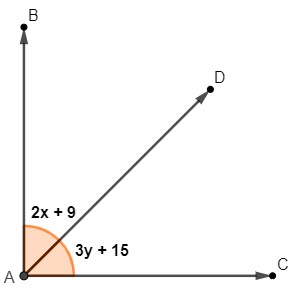
A) 25°
B) 28°
C) 30°
D) 32°
E) 35°
Alternativa B
Sabendo que os ângulos BAD e DAC são complementares, a soma deles é igual a 90°. Por outro lado, AD é bissetriz do ângulo BAC, então concluímos que BAD = DAC = 45°.
Temos o seguinte:
\(2x+9=45\ \)
\(2x=45-9\ \)
\(2x=36\)
\(x=\frac{36}{2}\)
\(x=18\)
Calculando o valor de y:
\(3y+15=45\)
\(3y=45-15\ \)
\(3y=30\ \)
\(y=\frac{30}{3}\)
\(y=10\ \)
A soma \(x+y=18+10=28°\)
(Uece) No quadrilátero XYZW, as medidas dos ângulos internos Z e W são respectivamente 128° e 76°. Se as bissetrizes dos ângulos internos X e Y cortam-se no ponto O, pode-se afirmar corretamente que a medida do ângulo XÔY é igual a
A) 156°
B) 78°
C) 204°
D) 102°
Alternativa D
A soma dos ângulos internos de um quadrilátero é sempre igual a 360°, então temos:
76 + 128 + 2x + 2y = 360
x + y = 78
A soma dos ângulos internos do triângulo XOY é igual a 180°, logo:
x + y + o = 180°
78 + o = 180°
o = 180° - 78°
o = 102°
O ângulo XÔY mede, portanto, 102°.
Sabendo que dois ângulos adjacentes somam 140°, a medida do ângulo formado por sua bissetriz é:
A) 100°
B) 80°
C) 70°
D) 55°
E) 45°
Alternativa C
A bissetriz divide os ângulos em duas partes iguais. Sendo assim, 140 : 2 = 70°. Logo, o ângulo formado pela bissetriz é de 70°.
Analise a imagem a seguir:
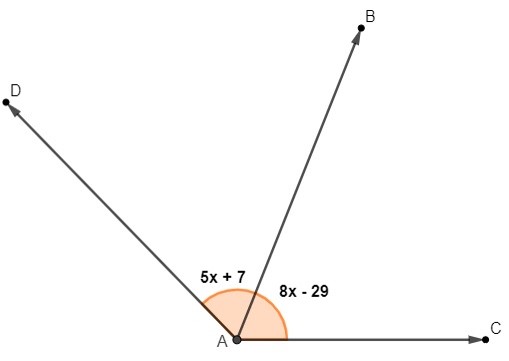
Sabendo que AB é bissetriz do ângulo DAC, a medida do ângulo DAB é:
A) 12°
B) 54°
C) 67°
D) 100°
E) 134°
Alternativa C
Como AB é bissetriz:
\(8x-29=5x+7\)
\(8x-5x=7+29\)
\(3x=36\)
\(x=\frac{36}{3}\)
\(x=12\)
Sabendo que x = 12, encontraremos o valor do ângulo DAB:
\(DAB=5x+7\)
\(DAB=5\cdot12+7\)
\(DAB=60+7\ \)
\(DAB=67°\)
A medida do ângulo suplementar ao ângulo AOC, sabendo que OB é a bissetriz desse ângulo, é igual a:
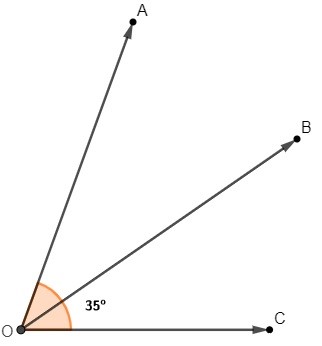
A) 180°
B) 145°
C) 110°
D) 70°
E) 35°
Alternativa C
Se que OB é a bissetriz, o ângulo AOB é também de 35°. Logo, o ângulo AOC é de 70°. Sendo assim, o suplementar desse ângulo é calculado por 180° - 70° = 110°. Portanto, o suplementar do ângulo AOC mede 110°.
No ângulo BAC, foi traçada a bissetriz AD. Posteriormente, no ângulo DAC foi traçada a bissetriz AE. Sabendo que o ângulo BAC mede 80°, a medida do ângulo BAE é:
A) 20°
B) 30°
C) 40°
D) 50°
E) 60°
Alternativa E
Sabemos que o ângulo BAC mede 80° e que ele foi dividido ao meio quando traçada a bissetriz AD, formando o ângulo BAD, medindo 40°, e o ângulo DAC, medindo também 40°. Porém, o ângulo DAC foi divido ao meio novamente, formando dois ângulos de 20°, sendo um deles o ângulo DAE.
O ângulo BAE é igual à soma da medida dos ângulos BAD + DAE, ou seja 40° + 20° = 60°.
Analise a imagem a seguir:
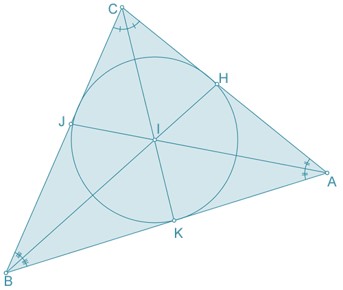
O ponto ao centro é conhecido como incentro do triângulo e ele é igual ao encontro das:
A) medianas do triângulo.
B) mediatrizes do triângulo.
C) alturas do triângulo.
D) bissetrizes do triângulo.
Alternativa D
Podemos perceber que todos os segmentos ao qual o ponto I pertence são bissetrizes do vértice. Logo, o incentro é igual ao encontro das bissetrizes do triângulo.
Analise a imagem a seguir:
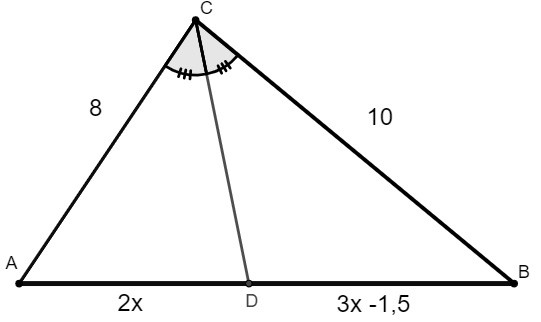
Sabendo que os lados foram dados em centímetros, a medida do segmento AB é:
A) 12,0
B) 12,5
C) 13,0
D) 13,5
E) 14,0
Alternativa D
Pelo teorema da bissetriz interna, temos que:
\(\frac{2x}{8}=\frac{3x-1,5}{10}\)
\(20x=8\cdot\left(3x-1,5\right)\)
\(20x=24x-12\)
\(12=24x-20\)
\(12=4x\)
\(\frac{12}{4}=x\)
\(x=3\)
Sabendo que x = 3, o segmento AB mede:
\(AB=2x+3x\ -1,5\)
\(AB=5x-1,5\ \)
\(AB=5\ \cdot3-1,5\ \)
\(AB=15-1,5\ \)
\(AB=13,5\)
