Exercícios sobre composição de três ou mais funções
A resolução de exercícios sobre composição de três ou mais funções assemelha-se à de questões com simples funções compostas, mas requer mais atenção e cuidado.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Se f(x) = x², g(x) = 2x e h(x) = – x³ + 2x² – x, determine o valor de f(g(h(2))).
Para resolver essa composição de funções, começaremos pela função composta mais interna, g(h(x)), ainda sem substituir o valor de x:
g(x) = 2x
g(h(x)) = 2.h(x)
g(h(x)) = 2.(– x³ + 2x² – x)
g(h(x)) = – 2.x³ + 4x² – 2xVamos agora calcular toda a composição das três funções f(g(h(x))):
f(x) = x²
f(g(h(x))) = [g(h(x))]²
f(g(h(x))) = [– 2.x³ + 4x² – 2x – 3]²
f(g(h(x))) = 4x6 – 16x5 + 24x4 – 16x3 + 4x2Podemos agora definir o valor de f(g(h(2))):
f(g(h(x))) = 4x6 – 16x5 + 24x4 – 16x3 + 4x2
f(g(h(2))) = 4.26 – 16.25 + 24.24 – 16.23 + 4.22
f(g(h(2))) = 4.64 – 16.32 + 24.16 – 16.8 + 4.4
f(g(h(2))) = 256 – 512 + 384 – 128 + 16
f(g(h(2))) = 16Portanto, o valor da composição das funções f(g(h(2))) é 16.
-
Questão 2
Sabendo que f o g = x² + 2x, que g o h = – 3x + 2 e que h o i = x + 1/x, determine f(g(h(i(x)))).
Podemos rescrever as funções compostas da seguinte forma:
f(g(x)) = x² + 2x
g(h(x)) = – 3x + 2
h(i(x)) = x + 1/x,Na composição f(g(h(i(x)))), podemos aplicar h(i(x)):
f(g(h(i(x)))) = f(g(x + 1/x)))
Mas sabemos que f(g(x)) = x² + 2x, sendo assim:
f(g(x)) = x² + 2x
f(g(x + 1/x))) = (x + 1/x)² + 2.(x + 1/x)
f(g(h(i(x)))) = x² + 2 + 1 + 2x + 2
x² x
f(g(h(i(x)))) = x4 + 2x² + 1 + 2x³ + 2x
x²
f(g(h(i(x)))) = x4 + 2x³ + 2x³ + 2x + 1
x²A composição das funções resulta em:
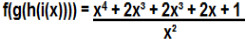
-
Questão 3
(Anglo) Sendo f e g funções de R em R, tais que f(x) = 3x – 1 e g(x) = x², o valor de f(g(f(1))) é:
a) 10
b) 11
c) 12
d) 13
e) 14
Resolveremos a função composta f(g(f(1))) “de dentro para fora”. Sendo assim, primeiramente faremos f(1):
f(x) = 3x – 1
f(1) = 3.1 – 1
f(1) = 3 – 1
f(1) = 2Agora faremos g(f(1)). Mas como f(1) = 2, faremos simplesmente g(2):
g(x) = x²
g(2) = 2²
g(2) = 4Para calcular f(g(f(1))), considerando que g(f(1)) = g(2) = 4, basta fazer f(4):
f(x) = 3x – 1
f(4) = 3.4 – 1
f(4) = 12 – 1
f(4) = 11A alternativa correta é a letra b.
-
Questão 4
(UFC) Considere a função f(x) = cx/(dx + 3), definida para todo número real x tal que dx + 3 ≠ 0, onde c e d são constantes reais. Sabendo que f(f(x)) = x e f5(3) = f(f(f(f(f(3))))) = – 3/5, podemos afirmar que c² + d² é igual a:
a) 5
b) 25
c) 61
d) 113
e) 181
De acordo com o enunciado do exercício, sabemos que f(f(x)) = x; sendo assim, podemos afirmar que f(f(3)) = 3, logo:
f(f(f(f(f(3))))) = – 3/5
f(f(f(3))) = – 3/5
f(f(f(3))) = – 3/5
f(3) = – 3/5 *Mas considerando a lei da função, temos que f(x) = cx/(dx + 3). Portanto, podemos também deduzir que:
f(x) = cx
dx + 3f(3) = c.3
d.3 + 3f(3) = 3.c
3.(d + 1)f(3) = c
d + 1Por *, temos que f(3) = – 3/5, sendo assim, chegamos à seguinte equação:
– 3 = c
5 d + 1– 3. (d + 1) = 5.c
– 3.d – 3 = 5.c
5c + 3d = – 3 **Reserve as equações f(3) = – 3/5 * e 5c + 3d = – 3 **, logo elas serão utilizadas. Por ora, vamos retomar a lei da função dada no enunciado. Se substituirmos x por f(x), teremos:
f(x) = cx
dx + 3f(f(x)) = c.f(x)
d.f(x) + 3x = c.f(x)
d.f(x) + 3E se substituirmos novamente o x? Onde houver x colocaremos 3 e, aplicando f(3) = – 3/5 *, obteremos:
3 = c.f(3)
d.f(3) + 33 = c. (-3/5)
d. (-3/5) = 33 = – 3.c
–3.d + 153 = – c
– d + 5– 3d + 15 = – c
c – 3d = – 15 ***Por 5c + 3d = – 3 ** e c – 3d = – 15 ***, temos o seguinte sistema que resolveremos pelo método da adição:
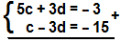
6c + 0.d = – 18
c = – 18
6
c = – 3Agora que encontramos c = – 3, substituiremos esse valor em c – 3d = – 15 ***:
c – 3d = – 15
- 3 - 3d = - 15
3 + 3d = 15
3d = 15 – 3
d = 12
3
d = 4Se c = – 3 e d = 4, podemos então calcular o valor de c² + d²:
c² + d² = (– 3)² + 4² = 9 + 16 = 25
Portanto, a alternativa correta é a letra b.