Exercícios sobre cone
Esta lista de exercícios é composta de questões envolvendo os principais conceitos sobre o cone, como o calculo de área total e o volume da geratriz.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Uma embalagem possui o formato de um cone. Sabendo que o raio da base desse cone é de 12 cm e sua altura é de 16 cm, então a área total dessa embalagem é:
(Use π = 3)
A) 1152 cm²
B) 1232 cm²
C) 1315 cm²
D) 1408 cm²
E) 1500 cm²
Alternativa A
Primeiro encontraremos a geratriz do cone:
g² = r² + h²
g² = 12² + 16²
g² = 144 + 256
g² = 400
g = √400
g = 20
Agora calcularemos a área total:
At = π · r (r + g)
At = 3 · 12 (12 + 20)
At = 36 ⸳ 32
At = 1152 cm²
-
Questão 2
Ao observar um cone, João fez três afirmativas:
I → O cone é um poliedro de base circular.
II → Devido à forma arredondada, o cone é um corpo redondo.
III → O cone possui a forma de um polígono.
Analisando as afirmativas feitas pelo João, podemos afirmar que:
A) Somente a I está correta.
B) Somente a II está correta.
C) Somente a III está correta.
D) Somente I e II estão corretas.
E) Somente II e III estão corretas.
-
Questão 3
(IDCAP) A figura abaixo é de um cone que tem o volume V = 37,68 cm³ e cujo raio da base é r = 3 cm. Considerando π = 3,14, a medida de g é:
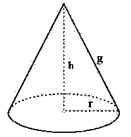
Então, a geratriz desse cone é igual a:
A) 4 cm
B) 3 cm
C) 28 cm
D) 5 cm
E) 113 cm
Alternativa D
Para encontrar a geratriz, é necessário encontrar o valor da altura, já que o raio é conhecido.
Sabemos que V = 37,68.
Então, temos que:
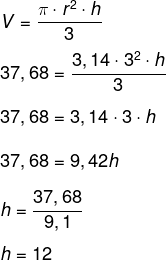
Agora sabemos que:
g² = h² + r²
g² = 4² + 3²
g² = 16 + 9
g² = 25
g = √25
g = 5
-
Questão 4
(Enem – PPL) Um arquiteto está fazendo um projeto de iluminação de ambiente e necessita saber a altura que deverá instalar a luminária ilustrada na figura.
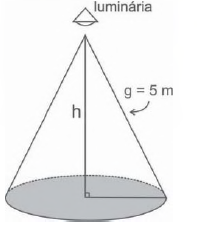
Sabendo que a luminária deverá iluminar uma área circular de 28,26 m², considerando π ≅ 3,14, a altura h será igual a
A) 3 m.
B) 4 m.
C) 5 m.
D) 9 m.
E) 16 m.
Alternativa B
Sabemos que:
A = π ⸳ r²
Calculando o raio, temos que:
28,26 = 3,14 . r²
r² = 28,26 : 3,14
r² = 9
r = √9
r = 3 metros
Agora, encontraremos a altura, pois sabemos que:
g² = h² + r²
5² = h² + 3²
25 = h² + 9
25 – 9 = h²
h² = 16
h = √16
h = 4 metros
-
Questão 5
Existem dois reservatórios de mesma altura e mesma base, mas o primeiro possui formato cilíndrico, com volume igual a V, então, o volume do segundo será igual a:
A) 3 V
B) 2 V
C) V
D) V : 2
E) V : 3
Alternativa E
Dado um cone com mesmo raio da base e mesma altura que o cilindro, seu volume será sempre a terça parte do volume do cilindro.
-
Questão 6
(Enem) A figura seguinte mostra um modelo de sombrinha muito usado em países orientais.
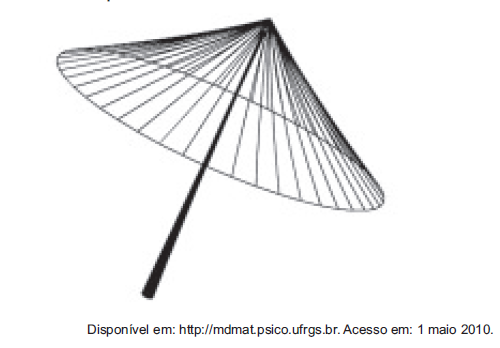
Esta figura é uma representação de uma superfície de revolução chamada de
A) pirâmide.
B) semiesfera.
C) cilindro.
D) tronco de cone.
E) cone.
Alternativa E
Essa figura possui o formado da superfície de revolução conhecido como cone.
-
Questão 7
Um recipiente no formato de um cone possui altura igual a 12 cm e o comprimento da circunferência da base igual a 52,7 cm. Utilizando π = 3,1, o volume desse recipiente, aproximadamente, é de:
A) 750 cm³
B) 784 cm³
C) 830 cm³
D) 896 cm³
E) 922 cm³
Alternativa D
Primeiro encontraremos o seu raio. Sabemos que o comprimento da circunferência é calculado por:
C = 2πr
Substituindo os valores dados, temos que:
52,7 = 2 ⸳ 3,1 · r
52,7 = 6,2
r = 52,7 : 6,2
r = 8,5
Agora, calcularemos o volume:
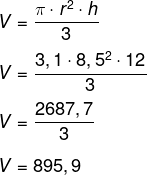
Então, a alternativa que mais se aproxima do volume encontrado é V = 896 cm³.
-
Questão 8
Uma fábrica de perfumes confecciona frascos no formato de um cone com altura h e raio r. Para melhorar as suas vendas, essa fábrica decidiu aprimorar o design dos frascos criando recipientes no formato de cilindro com altura h e raio r. Desse modo, sobre o volume do novo frasco, podemos afirmar que ele tem
A) a metade do volume do frasco cilíndrico.
B) o dobro do volume do frasco cilíndrico.
C) um terço do volume do frasco cilíndrico.
D) o triplo do volume do frasco cilíndrico.
E) o mesmo volume que o frasco cilíndrico.
Alternativa D
Dado o volume de um cone V, o cilindro que possui mesma altura e mesma base terá o volume igual ao triplo do volume do cone.
-
Questão 9
Um recipiente de vidro possui formato de um cone com raio da base igual a 12 cm e geratriz igual a 16 cm. Sabendo que, para produzir esse vidro, são gastos R$ 0,15 por cm², utilizando π = 3, o valor gasto para produzir um desses recipientes de vidro é:
A) R$ 108
B) R$ 125,12
C) R$ 151,20
D) R$ 175,30
E) R$ 192,45
Alternativa C
Calcularemos área total desse recipiente.
At = π · r (r + g)
At = 3 · 12 (12 + 16)
At = 36 ⸳ 28
At = 1008 cm²
Então, o valor gasto é:
0,15 ⸳ 10.008 = R$ 151,20
-
Questão 10
Julgue as afirmativas a seguir:
I → O cone é um corpo redondo.
II → O tronco de cone é obtido da secção de um cone.
III → O cone é um sólido de Platão.
Marque a alternativa correta:
A) Somente a I é falsa.
B) Somente a II é falsa.
C) Somente a III é falsa.
D) Todas são verdadeiras.
Alternativa C
-
I → Verdadeira. O cone, como o cilindro e a esfera, é conhecido como corpo redondo por possuir superfície com curvas.
-
II → Verdadeira. Se for realizada uma secção de um plano a qualquer altura do cone paralela à sua base, então encontraremos o tronco de cone.
-
III → Falsa. O cone não satisfaz a definição para que ele seja classificado como sólido de Platão, pois ele não é um poliedro.
-
-
Questão 11
(Enem) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.
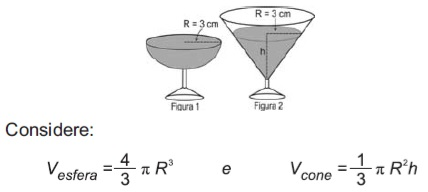
Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de
A) 1,33
B) 6,00
C) 12,00
D) 56,52
E ) 113,04
Alternativa B
Para que o volume seja o mesmo, basta igualar as equações, mas note que a equação dada é a da esfera. Como há um hemisfério, basta dividirmos essa fórmula por 2. Como 2 ⸳ 3 = 6, temos que:
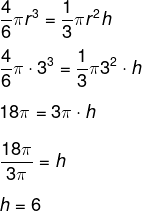
-
Questão 12
Em uma fábrica foi construído um reservatório no formato de um cone reto, com raio de 3 m e altura de 4 m. Para a conservação do reservatório, foi contratado um pintor, que cobra R$ 5 por m², para pintar a área externa e inclusive a base desse reservatório. Então. qual o valor gasto para pintar o reservatório todo? (Use π = 3.)
A) R$ 400
B) R$ 360
C) R$ 320
D) R$ 272
E) R$ 250
Alternativa B
Primeiro, calcularemos a geratriz:
g² = r² + h²
g² = 3² + 4²
g² = 9 + 16g² = 25
g = √25
g = 5
Agora, calculando a área total, temos que:
At = π · r (r + g)
At = 3 · 3 (3 + 5)
At = 9 ⸳ 8
At = 72 m²
Sabemos que, a cada metro quadrado, será cobrado R$ 5, então:
5 ⸳ 72 = 360