Exercícios sobre equação do 2° Grau
Uma das principais formas utilizadas para resolver exercícios sobre equação do 2° grau é através da fórmula de Bhaskara.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Resolva a equação do 2° grau 2x² + x – 3 = 0.
Uma das alternativas para solucionar equações do 2° grau é através da fórmula de Bhaskara. Para tanto, precisamos identificar os coeficientes da equação, que são a = 2, b = 1 e c = – 3.
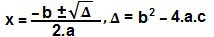
Δ = 1² – 4.2.(– 3)
Δ = 1 + 24
Δ = 25x = – 1 ± √25
2.2x = – 1 ± 5
4x' = – 1 + 5 = 4 = 1
4 4x'' = – 1 – 5 = – 6 = – 3
4 4 2As raízes da equação 2x² + x – 3 = 0 são 1 e – 3/2.
-
Questão 2
Determine o conjunto solução da equação – 3x² + 18x – 15 = 0.
Os coeficientes numéricos dessa equação do 2° grau são a = – 3, b = 18 e c = – 15. Observe que todos os coeficientes são múltiplos de 3, por isso podemos dividir todos por 3 para obter valores menores e, consequentemente, mais fáceis de calcular. Os novos coeficientes são: a = – 1, b = 6 e c = – 5. Ao realizar essa simplificação dos coeficientes, o resultado da equação permanece inalterado.
Vamos aplicar esses coeficientes na fórmula de Bhaskara:
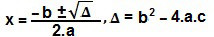
Δ = 6² – 4.(– 1).(– 5)
Δ = 36 – 20
Δ = 16x = – 6 ± √16
2.(– 1)x = – 6 ± 4
– 2x' = – 6 + 4 = – 2 = 1
– 2 – 2x'' = – 6 – 4 = – 10 = 5
– 2 – 2O conjunto solução é S = {1; 5}.
-
Questão 3
(Puc – Rio) As duas soluções de uma equação do 2° grau são – 1 e 1/3. Então a equação é:
Para encontrar a equação do 2° grau a partir de suas raízes, basta fazer:
(x – S1) · (x – S2) = 0
S1 e S2 são as raízes da equação. Vamos substituí-las na operação acima:
(x – (– 1)) · (x – (1/3)) = 0
(x + 1) · (x – (1/3)) = 0
x² – (1/3)x + x – 1/3 = 0
x² + (2/3)x – 1/3 = 0Podemos multiplicar toda a equação por 3:
3x² + 2x – 1 = 0
Portanto, a alternativa correta é a letra c.
-
Questão 4
(Cesgranrio) A maior raiz da equação – 2x² + 3x + 5 = 0 vale:
Para resolver essa equação do 2° grau, vamos utilizar a Fórmula de Bhaskara. Os coeficientes da equação são a = – 2, b = 3 e c = 5. Substituindo-os na fórmula, temos:
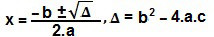
Δ = 3² – 4.(– 2).5
Δ = 9 + 40
Δ = 49x = – 3 ± √49
2.(– 2)x = – 3 ± 7
– 4x' = – 3 + 7 = 4 = – 1
– 4 – 4x'' = – 3 – 7 = – 10 = 2,5
– 4 – 4Encontramos duas raízes para a equação, x' = – 1 e x'' = 2,5; e a maior delas é x'' = 2,5. Portanto, a alternativa correta é a letra d.