Exercícios sobre equação biquadrada
Para resolver exercícios sobre equações biquadradas, devemos sempre substituir a incógnita da equação por outra letra, fazendo a seguinte relação x2 = y.
Publicado por: Naysa Crystine Nogueira OliveiraQuestões
-
Questão 1
(CMRJ) Dada a equação x4 + 4x2 - 45=0, podemos afirmar que:
a) tal equação possui 4 raízes reais.
b) duas de suas raízes são números racionais.
c) a soma das suas raízes reais é igual a −4.
d) o produto das suas raízes reais é igual a −5.
e) o produto das suas raízes reais é igual a −45.
Para resolver essa questão, devemos fatorar x4:
(x2)2 + 4x2 – 45=0
x2 . x2 + 4x2 – 45=0
Agora nomeie outra letra para x2 → x2 = y
y . y + 4y – 45=0
y 2 + 4y – 45=0
A equação encontrada é de segundo grau. Vamos resolvê-la utilizando a fórmula de Bhaskara:
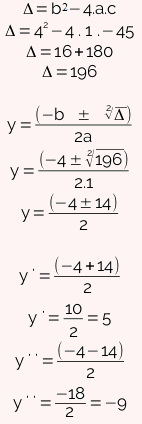
Agora que encontramos dois valores para y, devemos substitui-los na fórmula x2 = y para conhecermos as raízes de x.
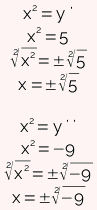
Como não existe raiz quadrada negativa no conjunto dos números reais, -9 não é solução da equação. Com isso, a alternativa correta para essa questão é a letra d, já que:
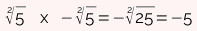
-
Questão 2
Resolva a equação 2x4 – 20x2 – 12 = 0.
Para solucionar essa questão, devemos fatorar x4:
2 . x2 . x2– 20x2 – 12 = 0.
Agora faça a substituição devida → x2 = y:
2y2– 20y – 12 = 0
A equação encontrada é de segundo grau. Vamos resolvê-la utilizando a fórmula de Bhaskara:
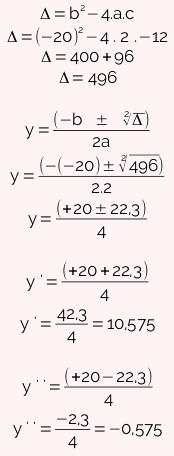
Devemos agora encontrar as raízes da equação para a incógnita x → x2 = y. Como y'' é negativo (-0,575), não será solução para a equação. Logo, aplicaremos a fórmula somente para y'.
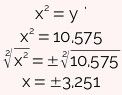
-
Questão 3
(FAAP-SP) Em R, resolver x4 - 3x2 – 4 = 0.
Fatore x4, transformando-o em: x2 . x2.
x2 . x2 - 3x2 – 4 = 0
Substitua x2 por y.
y. y – 3y – 4 = 0
y2 – 3y – 4 = 0
Utilizando a fórmula de Bhaskara, resolva a equação do segundo grau.
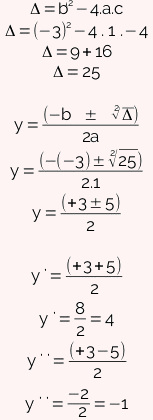
Como y'' é negativo, não iremos utilizá-lo para encontrar a resposta final. Substitua o valor de y' = 4 na fórmula x2 = y para encontrar as raízes reais de x.
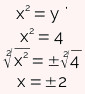
-
Questão 4
Verifique se o conjunto x = {+2, -2, + 1, -1} é solução da seguinte equação biquadrada:
x4 - 5x2 +4 = 0
Para verificar se os números do conjunto {+2, -2, + 1, -1} são soluções da equação, devemos substituir x pelos valores numéricos e verificar se encontramos ao final dos cálculos: 0 = 0. Caso isso aconteça, o número da substituição será raiz.
Substituindo x por + 2
x4 - 5x2 +4 = 0
24 – 5 . 22 + 4 = 0
16 - 20 + 4 = 0
16 – 16 = 0
0 = 0
Temos que +2 é solução da equação biquadrada.
Substituindo x por – 2
x4 - 5x2 +4 = 0
(-2)4 – 5 . ( - 2)2 + 4 = 0
+ 16 – 20 + 4 = 0
+ 16 – 16 = 0
0 = 0
O número –2 é solução da equação biquadrada.
Substituindo x por + 1
x4 - 5x2 +4 = 0
+14 – 5 . + 12 + 4 = 0
+1 – 5 + 4 = 0
- 4 + 4 = 0
0 = 0
+ 1 é solução da equação biquadrada.
Substituindo x por - 1
x4 - 5x2 +4 = 0
(-1)4 – 5 . (- 12) + 4 = 0
+1 – 5 . + 1 + 4 = 0
-4 + 4 = 0
0 = 0
O número -1 é solução da equação biquadrada.
Temos que todos os números {+2, -2, + 1, -1} são soluções da equação: x4 - 5x2 +4 = 0.