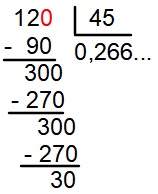Exercícios sobre fração geratriz
Desenvolvemos esta lista de exercícios sobre fração geratriz, a representação fracionária de uma dízima periódica, para você testar seus conhecimentos sobre o assunto.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Analise a fração a seguir:
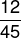
Podemos afirmar que ela é a fração geratriz da dízima:
-
Questão 2
(MS Concursos) Sejam x e y dois números reais, sendo x = 2,333... e y = 0,1212..., dízimas periódicas. A soma das frações geratrizes de x e y é:
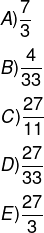
Alternativa C.
Primeiro encontraremos a fração geratriz de x e de y:
x = 2,333…
x = 2 + 0,333…
Na dízima 0,333…, o período é igual a 3. Por meio do método prático, para transformar em uma fração, o numerador será 3 e, como há um único algarismo no período, o denominador será 9.
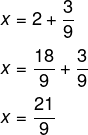
Agora a fração geratriz de y terá numerador igual a 12 (que é o seu período) e denominador igual a 99, já que há dois algarismos no período.
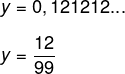
Vamos realizar, então, a soma x + y:
-
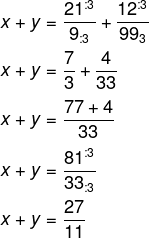
Questão 3
Sobre as dízimas, julgue as afirmativas a seguir:
I. A representação fracionária da dízima periódica é chamada de fração geratriz.
II. As dízimas não periódicas possuem fração geratriz.
III. Toda dízima periódica é um número racional.
Marque a alternativa correta:
Alternativa D.
I → Verdadeira, pois a fração geratriz é a representação fracionária da dízima.
II → Falsa, pois a dízima não periódica não possui representação fracionária, somente dízimas periódicas possuem.
III → Verdadeira, pois um número racional é aquele que possui representação fracionária, e a fração geratriz é essa representação.
-
Questão 4
Seja x = 1,123123… A diferença entre o numerador e o denominador da sua representação fracionária é:
Alternativa A.
Primeiro encontraremos a fração geratriz de x:
x = 1,123123…
x = 1+ 0,123123…
Na dízima periódica 0,123123…, 123 é o período e será o numerador da fração. Já o denominador será 999, pois há três algarismos no período.
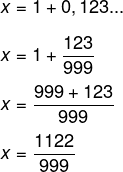
Com a fração geratriz, a diferença entre o numerador e o denominador será de:
1122 – 999 = 123
-
Questão 5
A fração geratriz de dízima periódica 3,151515… é igual a:
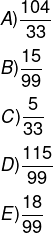
Alternativa A.
Seja x = 3,1515…, temos que:
-
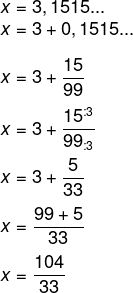
Questão 6
(TRT) Renato dividiu dois números inteiros positivos em sua calculadora e obteve como resultado a dízima periódica 0,454545… Se a divisão tivesse sido feita na outra ordem, ou seja, o maior dos dois números dividido pelo menor deles, o resultado obtido por Renato na calculadora teria sido:
Alternativa E.
Primeiro vamos encontrar a fração geratriz da dízima 0,454545… Como o período é 45 e é composto por dois algarismos, ele será o numerador, e o denominador será 99. O exercício propõe uma divisão entre o denominador e o numerador, logo:
99 : 45 = 2,2
-
Questão 7
A solução da expressão numérica a seguir é:
9 · (1,2525… + 0,888..)
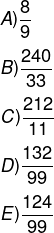
Alternativa C.
Para encontrar a solução, encontraremos a fração geratriz da dízima 1,252525…
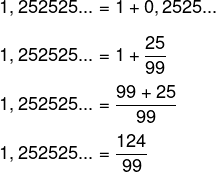
Também é necessário encontrar a fração geratriz da dízima 0,888…
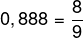
Agora, substituindo as dízimas pela sua fração geratriz, temos que:
-
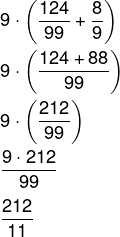
Questão 8
Analise os números reais a seguir:
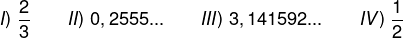
Podemos escrever como uma dízima periódica:
Alternativa B.
I → É uma dízima periódica. Se dividirmos 2 por 3, encontramos a dízima periódica 0,6666.
II → É uma dízima periódica composta. É possível perceber que, em sua parte decimal, há uma parte não periódica e uma parte periódica.
III → Não é uma dízima periódica.
IV → Não é uma dízima periódica, pois, se dividirmos 1 por 2, encontraremos um número decimal exato.
-
Questão 9
(Pref. de Niterói) Simplificando a expressão abaixo
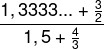
Obtém-se:
Alternativa B.
Primeiro encontraremos a fração geratriz da dízima 1,333..
1,333… = 1 + 0,333…
A dízima 0,333… possui período 3 e denominador 9, então:
-
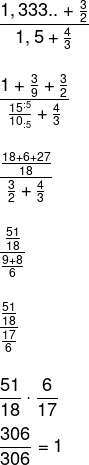
Questão 10
Durante os estudos dos números racionais, Eduardo encontrou como resultado de uma divisão o número 3,0121212… Com base no resultado encontrado por ele, julgue as afirmativas a seguir:
I. O resultado é um número racional.
II. O resultado é uma dízima periódica composta.
III. O resultado não pode ser representado como uma fração.
Marque a alternativa correta:
Alternativa C.
I → Verdadeira, pois as dízimas periódicas são números racionais.
II → Verdadeira, pois é possível perceber que, em sua parte decimal, há uma parte não periódica.
III → O resultado não pode ser representado como uma fração.
-
Questão 11
A fração geratriz da dízima 15,2222… é ?
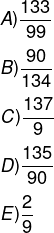
Alternativa C.
A fração geratriz de 0,222… possui numerador igual a 2 e denominador igual a 9, então:
-
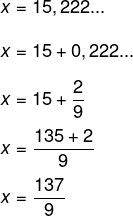
Questão 12
Sobre as dízimas, julgue as afirmativas a seguir:
I. Toda dízima possui uma fração geratriz.
II. Uma dízima pode ser um número racional ou irracional.
III. A representação decimal do número π é uma dízima periódica
Marque a alternativa correta:
Alternativa B.
I → Falsa, pois as dízimas não periódicas não podem ser representadas como fração.
II → Verdadeira, pois as dízimas periódicas são números racionais, e as dízimas não periódicas são números irracionais.
III → Falsa, pois π = 3,14159265…, que é uma dízima não periódica.
