Exercícios sobre função do 2º grau
Dada a função f (x) = x2 - 4x + 5 o valor de f(2) é:
A) 0.
B) 1.
C) 3.
D) 4.
E) 7.
Alternativa B.
Calculando f(2), temos que:
f(2) = 22 - 4 ⋅ 2 + 5
f(2) = 4 - 8 + 5
f(2) = - 4 + 5
f(2) = 1
Qual é o valor do discriminante da função x2 + 6x + 9 = 0?
A) 0.
B) 3.
C) 6.
D) 9.
E) 36.
Alternativa A.
Calculando o discriminante, temos que:
Δ = b2 - 4ac
a = 1, b = 6 e c = 9.
Δ = 62 -4 ⋅ 1 ⋅ 9
Δ = 36 - 36
Δ = 0
O gráfico da função f(x) = x2 - 5x + 6 possui como raiz os números naturais:
A) 1 e 6.
B) 2 e 3.
C) 3 e 5.
D) 1 e 5.
E) 2 e 4.
Alternativa B.
Δ = b2 - 4ac
a = 1, b = -5 e c = 6.
Δ = (-5)2 -4 ⋅ 1⋅ 6
Δ = 25 - 24
Δ = 1
Agora para calcular os zeros da função utilizaremos a fórmula de Bhaskara
\(x = \frac{-b \pm \sqrt{\Delta}}{2a} \)
\(x = \frac{5 \pm \sqrt{1}}{2 \cdot 1} \)
\(x = \frac{5 \pm 1}{2}\)
\(x_1 = \frac{5 + 1}{2} = \frac{6}{2} = 3\)
\(x_2 = \frac{5 - 1}{2} = \frac{4}{2} = 2 \)
As raízes da função são 2 e 3.
A concavidade da parábola da função f(x) = -3x2 + 2x + 1 é:
A) voltada para cima.
B) inexistente.
C) voltada para baixo.
D) vertical.
E) horizontal.
Alternativa C.
O que determina a concavidade da parábola é o valor do coeficiente a, que é igual a – 3; nesse caso, a parábola possui a concavidade voltada para baixo.
Os zeros da função quadrática f(x) = 2x2 - 8x são:
A) 0 e 2.
B) 2 e 4.
C) 0 e 4.
D) 2 e 8.
E) 0 e – 4.
Alternativa C.
Queremos que:
2x2 - 8x = 0
Colocando x em evidência:
x (2x - 8) = 0
Para que a multiplicação seja igual a 0, temos que:
x = 0
2x - 8 = 0
Então:
2x - 8 = 0
2x = 8
x = \(\frac{8}{2} \)
x = 4
Logo, as raízes são 0 e 4.
Um agricultor deseja construir um cercado retangular com 20 metros de arame. A área A(x), em função da largura x, é dada por A(x) = x (10 - x). A função é do 2º grau e representa:
A) um crescimento linear.
B) um valor constante.
C) uma parábola com concavidade para baixo.
D) uma função exponencial.
E) uma parábola com concavidade para cima.
Alternativa C.
Temos a função:
A(x) = x (10 - x)
Realizando o produto:
A(x) = 10x - x2
A(x) = -x2 + 10x
Sabemos que essa é uma função do 2º grau e possui como gráfico uma parábola; além disso, como a = -1, essa parábola possui concavidade para baixo.
A trajetória de uma bola chutada é descrita pela função h(t) = -5t2 + 20t, em que h(t) é a altura em metros e t é o tempo em segundos. A altura máxima atingida pela bola é:
A) 10 m.
B) 15 m.
C) 20 m.
D) 25 m.
E) 30 m.
Alternativa C.
Queremos calcular o vértice dessa parábola.
\(y_v = \frac{-\Delta}{4a}\)
Logo, temos que:
\(Δ=b^2-4ac\)
\(Δ=20^2-4 \cdot (-5) \cdot 0\)
\(Δ=400 \)
Então:
\(y_v = \frac{-400}{4 \cdot (-5)} \)
\(y_v = \frac{-400}{-20}\)
\(y_v=20\)
A função que representa o número de pessoas em um parque durante o dia é f(t) = -2t2 + 8t + 10, em que t é o tempo em horas após a abertura e f(t) é o número de pessoas no parque. Quantas pessoas estavam no parque após 2 horas da sua abertura?
A) 0
B) 2
C) 8
D) 10
E) 18
Alternativa E.
Queremos calcular f(2), então temos que:
f(2) = - 2 ⋅ 22 + 8 ⋅ 2 + 10
f(2) = - 2 ⋅ 4 + 8 ⋅ 2 + 10
f(2) = - 8 + 16 + 10
f(2) = 8 + 10
f(2) = 18
Um atleta arremessa uma bola cuja altura em metros é dada por f(x) = - 2x2 + 10x + 1, em que x é o tempo em segundos e f(x) é a altura da bola. Após quantos segundos aproximadamente a bola volta a tocar o solo?
A) 1 s.
B) 2 s.
C) 3 s.
D) 4 s.
E) 5 s.
Alternativa E.
Sabemos que a = - 2, b = 10 e c = 1, logo temos que:
\(\Delta = b^2 - 4ac\)
\(Δ=10^2-4 \cdot (-2) \cdot 1\)
\(Δ= 100 + 8\)
\(Δ=108\)
\(x = \frac{-b \pm \sqrt{\Delta}}{2a} \)
\(x = \frac{-10 \pm \sqrt{108}}{2 \cdot (-2)} \)
\(x = \frac{-10 \pm 10,39}{-4} \)
\(x - \frac{ -20,39}{-4}\)
\(x=5,1 s\)
Então, o tempo gasto é de aproximadamente 5 segundos.
Uma fábrica de chocolates descobriu que o lucro mensal L(x), em milhares de reais, depende do preço de venda x, em reais, de cada barra de chocolate, conforme a função:
L(x) = - 2x2 + 16x - 20
Qual deve ser o preço de venda de cada barra de chocolate para que a empresa obtenha o maior lucro possível?
A) 2 reais.
B) 4 reais.
C) 6 reais.
D) 8 reais.
E) 10 reais.
Alternativa B.
Queremos encontrar o valor do xv.
\(x_v = -\frac{b}{2a}\)
\(x_v = -\frac{16}{2 \cdot (-2)}\)
\(x_v = - \frac{16}{-4}\)
\(x_v=-(-4)=4\)
(Enem 2016) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = –2t2 + 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.
A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1 600 pessoas, e uma segunda dedetização precisou acontecer.
A segunda dedetização começou no:
A) 19º dia.
B) 20º dia.
C) 29º dia.
D) 30º dia.
E) 60º dia.
Alternativa B.
Queremos o valor de t para que – 2t2 + 120t = 1600. Ajustando a equação, os coeficientes são:
-2t2 + 120t - 1600 = 0
a = -2, b = 120 e c = -1600
Então, calculando o delta:
Δ = b2 - 4ac
Δ = 1202 - 4 ⋅ (-2) ⋅ (-1600)
Δ = 14400 - 12800
Δ = 1600
Agora aplicando a fórmula da Bhaskara, temos:
\(t = \frac{-b \pm \sqrt{\Delta}}{2a} \)
\(t = \frac{-120 \pm \sqrt{1600}}{2 \ \cdot \ (-2)}\)
\(t = \frac{-120 \pm 40}{-4} \)
\(t_1 = \frac{-120 + 40}{-4} = \frac{-80}{-4} = 20\)
\(t_2 = \frac{-120 - 40}{-4} = \frac{-160}{-4} = 40\)
Então a dedetização deve ocorrer após 20 dias.
Analise o gráfico da função a seguir:
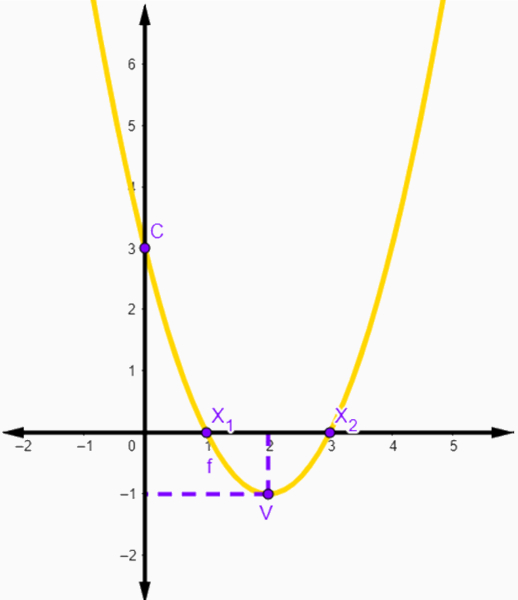
A função que está representada nesse gráfico é a função:
A) f(x) = x2 + 3x + 2
B) f(x) = x2 - 4x + 3
C) f(x) = x2 - x + 3
D) f(x) = 3x2 + x
E) f(x) = 3x2 - x + 2
Alternativa B.
Para encontrar o gráfico, conhecendo as duas raízes, temos que:
f(x) = (x - 1) (x - 3)
f(x) = x2 - 3x - x + 3
f(x) = x2 - 4x + 3
